5. Векторы, действия с векторами, скалярное произведение векторов, лз и лнз векторы

Вектор – направленный отрезок, заданный координатами начала и конца.

Алгебраическое определение вектора – вектор - направленный набор чисел, который называется координатным вектором.

Длинной или модулем вектора называется число, равное длине отрезка, изображающего вектор.

Коллинеарные векторы – векторы, лежащие на одной или параллельных прямых.

Компланарные векторы – векторы, лежащие в одной или параллельных плоскостях.

Ортогональные векторы – векторы, скалярное произведение которых равно нулю.

    Длина вектора, модуль (абсолютная величина):

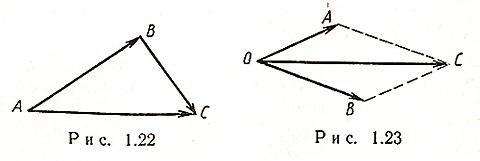
Сумма векторов:

   (правило треугольника) (рис. 1.22);

   (правило параллелограмма) (рис. 1.23);

   (правило многоугольника);

  (правило параллелепипеда, - диагональ).

 Разность векторов:

Формула вычитания векторов: (рис. 1.24).

Признак коллинеарности векторов:

Свойства векторов:

 Для любых векторов и любых чисел справедливы равенства

 Координатные формулы

 Пусть - взаимно ортогональные единичные векторы, имеющие направления координатных осей; - координаты вектора ; - координаты вектора ; или

Тогда:

Разность векторов:

Произведение вектора на число:

Длина вектора:

Если - начало вектора, - его конец, то

Скалярное произведение

 Скалярное произведение векторов и :

где - угол между векторами и ; если либо , то

Из определения скалярного произведения следует, что где, например, есть величина проекции вектора на направление вектора .

 Скалярный квадрат вектора:

 Свойства скалярного произведения:

Скалярное произведение в координатах

Если то

Угол между векторами

 

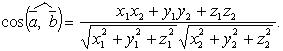
6. Векторное и смешанное произведения векторов

Векторное произведение

Векторное произведение векторов и - вектор, обозначаемый или для которого:

 1) ( - угол между векторами и , );

 2)

 3) тройка , , - правая.

Свойства векторного произведения:

если , то равен площади параллелограмма, построенного на приведенных к общему началу векторах и .

Векторное произведение в координатах

Если , то

или

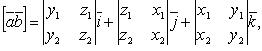
или

      В частности

 Смешанное произведение трех векторов

Определение:

 Свойства смешанного произведения:

- компланарны.

Если V - объем параллелепипеда, построенного на приведенных к общему началу векторах , и , то если тройка правая, и если тройка левая.

Смешанное произведение в координатах

Если то

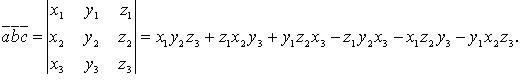
Линейная зависимость векторов

Выражение видаλ₁*A₁+λ₂*A₂+...+λ_n*A_n называется линейной комбинацией векторов A₁, A₂,...,A_n с коэффициентами λ_1, λ₂,...,λ_n.

Определение линейной зависимости системы векторов

Система векторов A₁, A₂,...,A_n называется линейно зависимой, если существует ненулевой набор чисел λ_1, λ₂,...,λ_n, при котором линейная комбинация векторов λ₁*A₁+λ₂*A₂+...+λ_n*A_n равна нулевому вектору, то есть система уравнений: A₁x₁+A₂x₂+...+A_nx_n =Θ имеет ненулевое решение. Набор чисел λ_1, λ₂,...,λ_n является ненулевым, если хотя бы одно из чисел λ_1, λ₂,...,λ_n отлично от нуля.

Определение линейной независимости системы векторов

Система векторов A₁, A₂,...,A_n называется линейно независимой, если линейная комбинация этих векторов λ₁*A₁+λ₂*A₂+...+λ_n*A_n равна нулевому вектору только при нулевом наборе чисел λ_1, λ₂,...,λ_n, то есть система уравнений: A₁x₁+A₂x₂+...+A_nx_n =Θ имеет единственное нулевое решение.

Свойства систем векторов

Свойство (1) Если система векторов линейно зависимая, то хотя бы один из векторов разлагается по остальным и, наоборот, если хотя бы один из векторов системы разлагается по остальным, то система векторов линейно зависимая.

Свойство (2) Если какая-либо подсистема векторов линейно зависимая, то и вся система линейно зависимая.

Свойство (3) Если система векторов линейно независимая, то любая ее подсистема линейно независимая.

Свойство (4) Любая система векторов, содержащая нулевой вектор, линейно зависимая.

Свойство (5) Система m-мерных векторов всегда является линейно зависимой, если число векторов n больше их размерности (n>m).