1. Матрицы: определение и свойства.

Прямоугольной матрицей размера m´n называется совокупность mn чисел, расположенных в виде прямоугольной таблицы, содержащей m строк и n столбцов. Мы будем записывать матрицу в виде

                                                                 (4.1)

или сокращенно в виде A = (a_{i j}) (i = ; j = ). Числа a_{i j}, составляющие данную матрицу, называются ее элементами; первый индекс указывает на номер строки, второй - на номер столбца. Две матрицы A = (a_{i j}) и B = (b_{i j}) одинакового размера называются равными, если попарно равны их элементы, стоящие на одинаковых местах, то есть A = B, если a_{i j} = b_{i j}.

Матрица, состоящая из одной строки или одного столбца, называется соответственно вектор-строкой или вектор-столбцом. Вектор-столбцы и вектор-строки называют просто векторами.

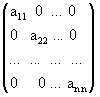
Матрица, состоящая из одного числа, отождествляется с этим числом. Матрица размера m´n, все элементы которой равны нулю, называются нулевой матрицей и обозначается через 0. Элементы матрицы с одинаковыми индексами называют элементами главной диагонали. Если число строк матрицы равно числу столбцов, то есть m = n, то матрицу называют квадратной порядка n. Квадратные матрицы, у которых отличны от нуля лишь элементы главной диагонали, называются диагональными матрицами и записываются так:

.

Если все элементы a_{i i} диагональной матрицы равны 1, то матрица называется единичной и обозначается буквой Е:

                                                                          .

Квадратная матрица называется треугольной, если все элементы, стоящие выше (или ниже) главной диагонали, равны нулю. Транспонированием называется такое преобразование матрицы, при котором строки и столбцы меняются местами с сохранением их номеров. Обозначается транспонирование значком Т наверху.

Пусть дана матрица (4.1). Переставим строки со столбцами. Получим матрицу

,

которая будет транспонированной по отношению к матрице А. В частности, при транспонировании вектора-столбца получается вектор-строка и наоборот.

Свойства транспонированных матриц.

1). Если E-единичная матрица, то E=E^T.

2). Двукратное транспонирование не изменяет матрицу (A^T)^T=A.

3). Транспонирование суммы матриц равносильно сложению транспонированных матриц: (A+B)^T=A^T+B^T

4).Транспонирование произведения матриц равносильно умножению транспонированных матриц: .

5). Транспонирование обратной матрицы равносильно вычислению обратной к транспонированной матрице: (A^-1)^T=(A^T)^-1 .

6). Если транспонированная матрица A^T совпадает с данной матрицей A, то матрица A называется симметрической.

Матрица называется обратной к данной матрице A, если их произведение равно единичной матрице:

 

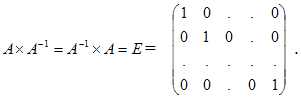
Вырожденной квадратной матрицей  называется такая матрица, определитель которой равен нулю. Матрица, определитель которой не равен 0, называется невырожденной. Для того, чтобы матрица A имела обратную матрицу, необходимо и достаточно, чтобы она была невырожденной. Для вычисления обратной матрицы к матрице А составим матрицу А* (присоединенную) из алгебраических дополнений матрицы А:

 

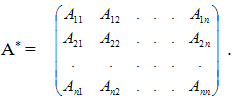
Матрицу транспонируем и каждый элемент разделим на определитель |A|. Нетрудно показать, что построенная таким образом матрица:

будет обратной к матрице А.

Определитель k-ого порядка, составленный из элементов матрицы A, лежащих на пересечении каких-либо ее k строк и k столбцов, называется минором k-ого порядка матрицы A.

Если матрица A имеет хотя бы один минор r-ого порядка не равный нулю, а все миноры (r+1)-го порядков равны нулю, то r называется рангом матрицы A.

Преобразования, не меняющие ранг матрицы, называются элементарными. К ним относятся:  1). Умножение строки или столбца на число, не равное нулю.  2). Перестановка строк или столбцов местами.  3). Прибавление к элементам одной строки или столбца элементов другой строки или столбца, умноженных на одно и то же число.  4). Вычеркивание строки или столбца, состоящего из нулей.

Сложение матриц.

Суммой матриц одной и той же размерности называется матрица размерности , каждый элемент которой представляет собой сумму соответствующих элементов матриц A и B:

Матрицы разных размерностей складывать нельзя.

Свойства сложения матриц. 1. Коммутативность. A+B=B+A 2. Ассоциативность. (A+B)+C=A+(B+C)

Умножение матриц.

Произведением матрицы А на число l называется матрица, элементы которой получаются из соответствующих элементов матрицы А умножением на число l: l A = (l a_{i j}).

Произведение АВ матрицы А на матрицу В определяется в предположении, что число столбцов матрицы А равно числу строк матрицы В.

Произведение матриц существует только тогда, когда число столбцов первой матрицы равно числу строк второй матрицы.

Произведением двух матриц А = (a_{i j}) и B = (b_{j k}), где i = , j= , k= , заданных в определенном порядке АВ, называется матрица С = (c _{i k}), элементы которой определяются по следующему правилу:

c _{i k} = a_{i 1} b_{1 k} + a_{i 2} b_{2 k} +... + a_{i m} b_{m k} = a_{i s} b_{s k}.                    (4.2)

Иначе говоря, элементы матрицы-произведения определяются следующим образом: элемент i-й строки и k-го столбца матрицы С равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы k-го столбца матрицы В.

Свойства действий над матрицами:

1. АЕ=А

2. А+В=В+А

3. АВ не равно ВА

4. (А+В)С=АС+ВС

5. (А^т)^т=А

6. (А+В)^т=А^т+В^т

7. (АВ)^т=А^тВ^т