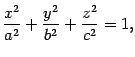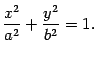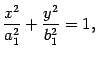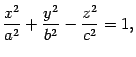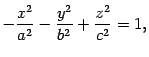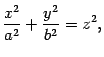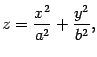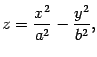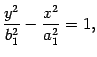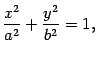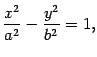19. Поверхности второго порядка

Пусть в пространстве задана прямоугольная декартова система координат.

        Определение 13.1   Поверхностью второго порядка называется поверхность, определяемая уравнением

(13.1)

где -- вещественные числа, причем хотя бы одно из чисел

отлично от нуля.         

поверхности второго порядка, за исключением случаев сильного вырождения, можно разделить на пять классов: эллипсоиды, гиперболоиды, параболоиды, конусы и цилиндры. Для каждой из поверхностей существует декартова прямоугольная система координат, в которой поверхность задается простым уравнением, называемым каноническим уравнением.

Определение 13.2   Сферой называется геометрическое место точек пространства, равноудаленных от фиксированной точки, называемой центром.         

        Теорема 13.1   Сфера радиуса с центром в точке имеет уравнение

(13.2)

Доказательство аналогично доказательству теоремы 3.1.

        Пример 13.1   Нарисуйте сферу

Решение. Выделив полные квадраты (пример 12.1), получим

Значит, центром сферы является точка , радиус сферы равен 2.

Для ее изображения нарисуем сечения сферы плоскостями, проходящими через центр и параллельными координатным плоскостям. Каждое такое сечение будет окружностью радиуса 2 с центром в точке (рис 4.1).

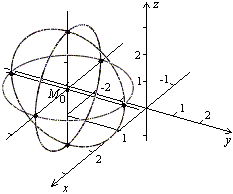
Рис.13.1.Сфера, изображенная сечениями

Более "художественное" изображение сферы приведено на рисунке 13.2

Рис.13.2.Сфера

Определение 13.3   Эллипсоидом называется поверхность, каноническое уравнение которой имеет вид

(13.3)

где , , -- положительные числа.         

Исследуем форму эллипсоида. Из уравнения (13.3) видно, что координаты точек поверхности ограничены: , , .

Эллипсоид обладает тремя плоскостями симметрии, тремя осями симметрии и центром симметрии. Ими служат соответственно координатные плоскости, координатные оси и начало координат. Доказывается это так же, как в предложении 12.1.

Для выяснения формы эллипсоида рассмотрим его сечения плоскостями. Найдем линию пересечения эллипсоида с плоскостью . Так как любая точка плоскости имеет нулевую третью координату, , то координаты точек эллипсоида на плоскости удовлетворяют уравнению

(13.4)

По теореме 12.2 получаем, что линия пересечения является эллипсом с полуосями и (рис. 13.3).

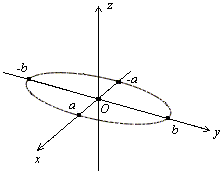
Рис.13.3.Сечение плоскостью

Аналогично, сечение в плоскости дает эллипс

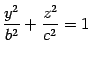
с полуосями и , а сечение плоскостью -- эллипс

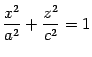
с полуосями и (рис. 13.4)

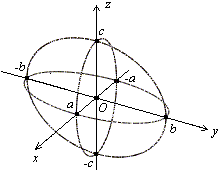
Рис.13.4.Сечения эллипсоида координатными плоскостями

Нарисованный "каркас" из сечений уже дает представление об эллипсоиде. Но чтобы выяснить, как ведет себя поверхность между нарисованными кривыми, рассмотрим сечение эллипсоида плоскостью . Эта плоскость параллельна плоскости и пересекает ось в точке . Уравнения этой линии

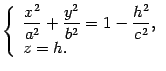
Очевидно, что если , то ни одна точка пространства не может удовлетворять этой системе: в левой части первого уравнения стоит неотрицательное число, а в правой -- отрицательное.

Если , то сечении получим лишь одну точку или в зависимости от знака .

Пусть . Тогда первое уравнение преобразуем к виду

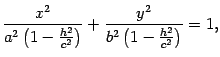
то есть к виду

(13.5)

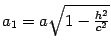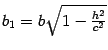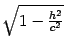где , . Уравнение (13.5) является уравнением эллипса, подобного эллипсу, задаваемому уравнением (13.4), с коэффициентом подобия и полуосями и . Ясно, что сечение плоскостью является таким же эллипсом, расположенным симметрично первому относительно плоскости . Нарисуем эти сечения (рис. 13.5).

Рис.13.5.Дополнительные сечения эллипсоида

Таким образом, весь эллипсоид составлен из эллипсов, лежащих в плоскостях, параллельных плоскости и подобных эллипсу в плоскости . Рисунок 13.6 дает более привычное глазу изображение эллипсоида.

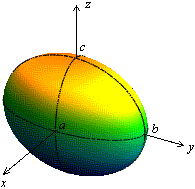
Рис.13.6.Эллипсоид

Так же, как для эллипса, точки пересечения эллипсоида с координатными осями называются вершинами эллипсоида, центр симметрии -- центром эллипсоида. Числа , , называются полуосями. Если полуоси попарно различны, то эллипсоид называется трехосным.

Если две полуоси равны друг другу, то эллипсоид называется эллипсоидом вращения. Эллипсоид вращения может быть получен вращением эллипса вокруг одной из осей. Например, если , то все сечения эллипсоида плоскостями , , будут окружностями. Сам эллипсоид может быть получен из эллипса

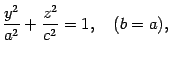
лежащего в плоскости , при вращении его вокруг оси (рис. 13.7).

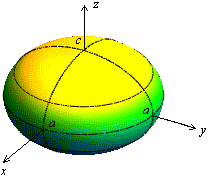
Рис.13.7.Эллипсоид вращения

Определение 13.4   Однополостным гиперболоидом называется поверхность, каноническое уравнение которой имеет вид

(13.6)

где , ,  -- положительные числа.         

Исследуем форму однополостного гиперболоида. Так же, как эллипсоид, он имеет три плоскости симметрии, три оси симметрии и центр симметрии. Ими являются соответственно координатные плоскости, координатные оси и начало координат.

Для построения гиперболоида найдем его сечения различными плоскостями. Найдем линию пересечения с плоскостью . На этой плоскости , поэтому

Это уравнение на плоскости задает эллипс с полуосями и (рис. 13.8). Найдем линию пересечения с плоскостью . На этой плоскости , поэтому

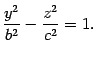
Это уравнение гиперболы на плоскости , где действительная полуось равна , а мнимая полуось равна . Построим эту гиперболу (рис. 13.8).

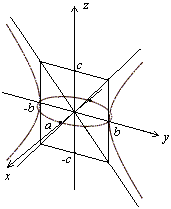
Рис.13.8.Сечения однополостного гиперболоида двумя плоскостями

Сечение плоскостью также является гиперболой с уравнением

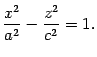
Нарисуем и эту гиперболу, но чтобы не перегружать чертеж дополнительными линиями, не будем изображать ее асимптоты и уберем асимптоты в сечении плоскостью (рис. 13.9).

Найдем линии пересечения поверхности с плоскостями , . Уравнения этих линий

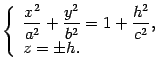
Первое уравнение преобразуем к виду

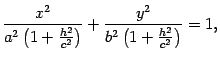
то есть к виду

(13.7)

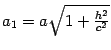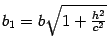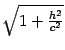где , . Уравнение (13.7) является уравнением эллипса, подобного эллипсу в плоскости , с коэффициентом подобия и полуосями и . Нарисуем полученные сечения (рис. 13.9).

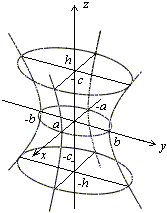
Рис.13.9.Изображение однополостного гиперболоида с помощью сечений

Привычное для глаза изображение однополостного гиперболоида приведено на рисунке 13.10.

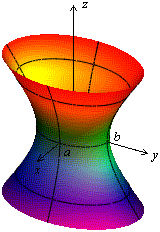
Рис.13.10.Однополостный гиперболоид

Если в уравнении (13.6) , то сечения гиперболоида плоскостями, параллельными плоскости , являются окружностями. В этом случае поверхность называется однополостным гиперболоидом вращения и может быть получена вращением гиперболы, лежащей в плоскости , вокруг оси (рис. 13.11).

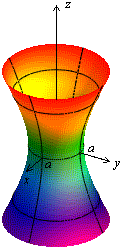
Рис.13.11.Однополостный гиперболоид вращения

        Определение 13.5   Двуполостным гиперболоидом называется поверхность, каноническое уравнение которой имеет вид

(13.8)

где , ,  -- положительные числа.         

Исследуем форму двуполостного гиперболоида. Так же, как эллипсоид и однополостный гиперболоид, он имеет три плоскости симметрии, три оси симметрии и центр симметрии. Ими являются соответственно координатные плоскости, координатные оси и начало координат.

Для построения гиперболоида найдем его сечения различными плоскостями. Найдем линию пересечения с плоскостью . На этой плоскости , поэтому

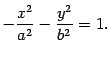
Координаты ни одной точки плоскости не могут удовлетворять данному уравнению. Следовательно, двуполостный гиперболоид не пересекает эту плоскость. Найдем линию пересечения с плоскостью . На этой плоскости , поэтому

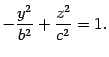
Это уравнение гиперболы на плоскости , где действительная полуось равна , а мнимая полуось равна . Построим эту гиперболу (рис. 13.12).

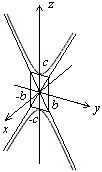
Рис.13.12.Сечения двуполостного гиперболоида плоскостью

Сечение плоскостью также является гиперболой, с уравнением

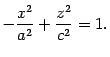
Нарисуем и эту гиперболу, но чтобы не перегружать чертеж дополнительными линиями, не будем изображать ее асимптоты и уберем асимптоты в сечении плоскостью (рис. 13.13).

Найдем линии пересечения поверхности с плоскостями , . Уравнения этих линий

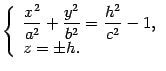
Очевидно, что ни одна точка не может удовлетворять этим уравнениям, если . Если или , то плоскость имеет с исследуемой поверхностью только одну точку или . Эти точки называются вершинами гиперболоида.

Пусть . Первое уравнение преобразуем к виду

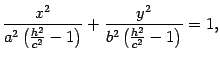
то есть к виду

(13.9)

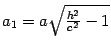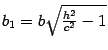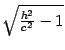где , . Уравнение (13.9) является уравнением эллипса, подобного эллипсу в плоскости , с коэффициентом подобия и полуосями и . Нарисуем полученные сечения (рис. 13.13).

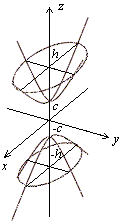
Рис.13.13.Изображение двуполостного гиперболоида с помощью сечений

Привычное для глаза изображение двуполостного гиперболоида приведено на рисунке 13.14.

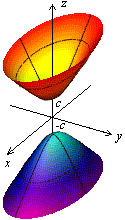
Рис.13.14.Двуполостный гиперболоид

Если в уравнении (13.8) , то сечения гиперболоида плоскостями, параллельными плоскости , являются окружностями. В этом случае поверхность называется двуполостным гиперболоидом вращения и может быть получена вращением гиперболы, лежащей в плоскости , вокруг оси (рис 4.15).

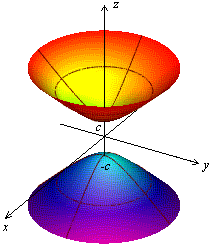
Рис.13.15.Двуполостный гиперболоид вращения

Определение 13.6   Конусом второго порядка называется поверхность, уравнение которой в некоторой декартовой системе координат имеет вид

(13.10)

где , ,  -- положительные числа.         

        Замечание 13.1   С математической точки зрения поверхность (13.10) лучше определять с помощью уравнения

(13.11)

так как в нем меньше параметров, но при этом, во-первых, теряется аналогия с уравнениями предыдущих поверхностей, а во-вторых, если считать, что величины , , , , имеют размерность длины, то в уравнении (13.11) размерности правой и левой части не согласуются.         

Для краткости в дальнейшем конус второго порядка будем называть просто конус. Исследуем форму конуса. Так же, как эллипсоид и гиперболоиды, он имеет три плоскости симметрии, три оси симметрии и центр симметрии. Ими являются соответственно координатные плоскости, координатные оси и начало координат.

Для построения конуса найдем его сечения различными плоскостями. Найдем линию пересечения с плоскостью . На этой плоскости , поэтому

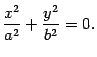
Координаты только одной точки плоскости могут удовлетворять данному уравнению, а именно, начала координат. Найдем линию пересечения с плоскостью . На этой плоскости , поэтому

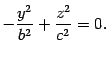
Это уравнение пары прямых на плоскости . Построим эти прямые (рис. 13.16). Сечение плоскостью также является парой прямых с уравнением . Нарисуем и эти прямые (рис. 13.16).

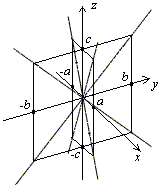
Рис.13.16.Сечения конуса координатными плоскостями

Найдем линии пересечения поверхности с плоскостями , . Уравнения этих линий

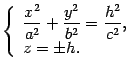
Первое уравнение преобразуем к виду

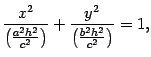
то есть к виду

(13.12)

где , . Уравнение (13.12) является уравнением эллипса. Нарисуем полученные сечения (рис. 13.17).

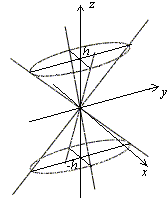
Рис.13.17.Изображение конуса с помощью сечений

Привычное для глаза изображение приведено на рисунке 13.18.

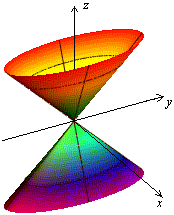
Рис.13.18.Конус

Точка пересечения конуса с плоскостью называется вершиной конуса.

Если в уравнении (13.10) , то сечения конуса плоскостями параллельными плоскости являются окружностями. В этом случае поверхность называется прямым круговым конусом и может быть получена вращением прямой, лежащей в плоскости , вокруг оси . Именно с таким конусом мы имеем дело в школьном курсе математики.

Определение 13.7   Эллиптическим параболоидом называется поверхность, уравнение которой в некоторой декартовой системе координат имеет вид

(13.13)

где и -- положительные числа.         

Исследуем форму эллиптического параболоида. Он имеет две плоскости симметрии и ось симметрии. Ими являются соответственно координатные плоскости , и координатная ось .

Для построения эллиптического параболоида найдем его сечения различными плоскостями. Найдем линию пересечения с плоскостью . На этой плоскости , поэтому

Координаты только одной точки плоскости могут удовлетворять данному уравнению, а именно, начала координат. Найдем линию пересечения с плоскостью . На этой плоскости , поэтому

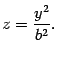
Это уравнение параболы на плоскости . Построим ее (рис. 13.19). Сечение плоскостью также является параболой. Нарисуем и ее (рис. 13.19). Найдем линии пересечения поверхности с плоскостью . Уравнения этой линии

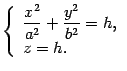
Очевидно, что только одна точка (начало координат) удовлетворяет этим уравнениям, если . Эта точка называется вершиной параболоида.

Пусть . Первое уравнение преобразуем к виду

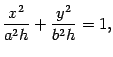
то есть к виду

(13.14)

где , . Уравнение (13.14) является уравнением эллипса. Нарисуем полученное сечение (рис. 13.19). При плоскость поверхность не пересекает.

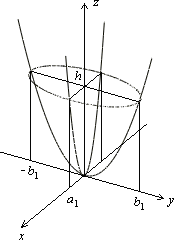
Рис.13.19.Сечения эллиптического параболоида координатными плоскостями

Найдем сечения параболоида плоскостями , параллельными плоскости . Линии этих сечений удовлетворяют уравнениям

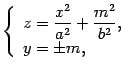
и являются параболами, такими же, как в плоскости , только сдвинутыми вверх на величину , их вершины при таком сдвиге лежат на параболе, получившейся в сечении плоскостью (рис. 13.20).

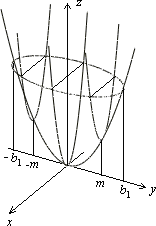
Рис.13.20.Дополнительные сечения параболоида

Следовательно, вся поверхность может быть получена движением параболы, лежащей в плоскости . Парабола должна двигаться так, чтобы ее плоскость была параллельна плоскости , а вершина скользила по параболе в плоскости .

Привычное для глаза изображение приведено на рисунке 13.21.

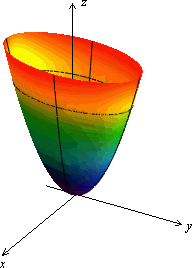
Рис.13.21.Эллиптический параболоид

Если в уравнении (13.13) , то сечения плоскостями, параллельными плоскости , являются окружностями. В этом случае поверхность называется параболоидом вращения и может быть образована вращением параболы, лежащей в плоскости , вокруг оси (рис. 13.22).

Рис.13.22.Параболоид вращения

        Определение 13.8   Гиперболическим параболоидом называется поверхность, уравнение которой в некоторой декартовой системе координат имеет вид

(13.15)

где и -- положительные числа.         

Исследуем форму гиперболического параболоида. Так же, как и эллиптический параболоид, он имеет две плоскости симметрии и ось симметрии. Ими являются соответственно координатные плоскости , и координатная ось .

Для построения гиперболического параболоида найдем его сечения различными плоскостями. Найдем линию пересечения с плоскостью . На этой плоскости , поэтому

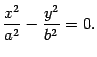
Это уравнение определяет на плоскости пару прямых , изображенных на рисунке 13.23.

Найдем линию пересечения с плоскостью . На этой плоскости , поэтому

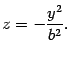
Это уравнение на плоскости задает параболу, ветви которой направлены вниз. Построим ее (рис. 13.23). Сечение плоскостью также является параболой

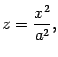
но ее ветви направлены вверх. Нарисуем и ее (рис. 13.23).

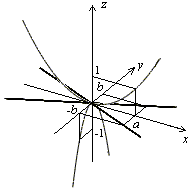
Рис.13.23.Сечения гиперболического параболоида координатными плоскостями

Найдем линии пересечения поверхности с плоскостью , . Уравнения этой линии

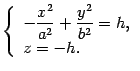
Первое уравнение преобразуем к виду

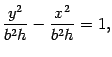
то есть к виду

(13.16)

где , . Уравнение (13.16) является уравнением гиперболы. Ее действительная ось параллельна оси , а мнимая -- оси . Полуоси равны соответственно и . Нарисуем полученное сечение, но чтобы не перегружать рисунок линиями, асимптоты изображать не будем (рис. 13.24).

Найдем линии пересечения с плоскостями , параллельными плоскости . Уравнения этих линий

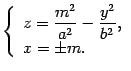
Первое из этих уравнений является уравнением параболы, такой же, как и в сечении плоскостью , только сдвинутой вдоль оси на величину вверх. Эти параболы изображены на рисунке 13.24.

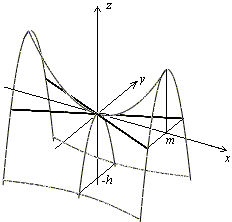
Рис.13.24.Изображение гиперболического параболоида с помощью сечений

Так как -- произвольное число, то вся поверхность может быть получена движением параболы, лежащей в плоскости . Передвигать параболу нужно так, чтобы ее плоскость оставалась параллельной плоскости , а вершина скользила по параболе в плоскости .

Плоскость , , пересекает поверхность по гиперболе, но в отличие от гиперболы (13.16), ее действительная ось параллельна теперь оси , а мнимая -- оси (рис. 13.25).

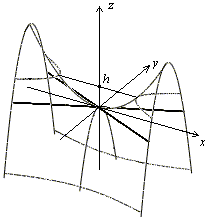
Рис.13.25.Дополнительное сечение

Привычное для глаза изображение приведено на рисунке 13.26.

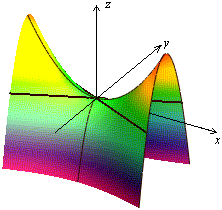
Рис.13.26.Гиперболический параболоид

Определение 13.9   Цилиндрической поверхностью называется геометрическое место параллельных прямых, пересекающих данную линию. Эта линия называется направляющей, а параллельные прямые -- образующими.         

Рассмотрим уравнение вида

(13.17)

и покажем, что оно определяет цилиндрическую поверхность с образующими, параллельными оси . Пусть  -- некоторая точка, координаты которой удовлетворяют уравнению (13.17). Поскольку в это уравнение не входит явно переменная , ему будут удовлетворять координаты всех точек , где  -- любое число. Следовательно, при любом точка лежит на поверхности, определяемой уравнением (13.17). Отсюда следует, что на поверхности целиком лежит прямая, проходящая через точку параллельно оси . А это означает, что поверхность, определяемая уравнением (13.17), составлена из прямых, параллельных оси , то есть она является цилиндрической поверхностью.

Заметим, что на плоскости уравнение (13.17) определяет направляющую рассматриваемой цилиндрической поверхности.

Итак, делаем вывод, что если уравнение поверхности не содержит в явном виде какой-либо переменной, то это уравнение определяет в пространстве цилиндрическую поверхность с образующими, параллельными оси отсутствующего переменного и направляющей, которая в плоскости двух других переменных имеет то же самое уравнение.

Нас будут интересовать только те цилиндрические поверхности, которые являются поверхностями второго порядка, а это значит, что уравнение  (13.17), их задающее будет иметь вид (13.1).

        Определение 13.10   Поверхность, которая в некоторой декартовой системе координат задается уравнением

(13.18)

называется эллиптическим цилиндром, поверхность, которая задается уравнением

(13.19)

называется гиперболическим цилиндром, а которая задается уравнением

(13.20)

называется параболическим цилиндром.         

Для того чтобы построить поверхность, задаваемую уравнением (13.18), или уравнением (13.19), или (13.20), достаточно нарисовать на плоскости направляющую, уравнение которой на этой плоскости совпадает с уравнением самой поверхности, и затем через точки направляющей провести образующие параллельно оси . Для наглядности следует построить также одно-два сечения плоскостями, параллельными плоскости . В каждом таком сечении получим такую же кривую, как и исходная направляющая. Изображения этих цилиндров сечениями приведены на рисунках 13.27, 13.29 и 13.31, а их объемные изображения -- на рисунках 13.28, 13.30 и 13.32.

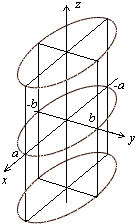
Рис.13.27.Изображение эллиптического цилиндра с помощью сечений

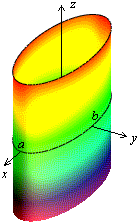
Рис.13.28.Эллиптический цилиндр

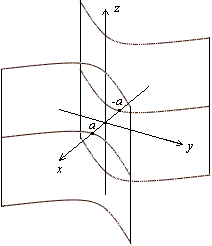
Рис.13.29.Изображение гипербоического цилиндра с помощью сечений

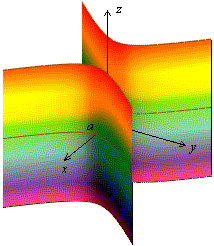
Рис.13.30.Гиперболический цилиндр

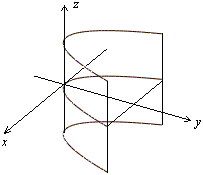
Рис.13.31.Изображение параболического цилиндра с помощью сечений

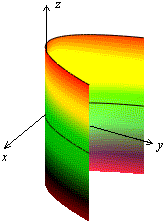
Рис.13.32.Параболический цилиндр

Параллельный перенос системы координат

Так же как и на плоскости, в пространстве можно выполнить параллельный перенос системы координат. Формулы и их доказательства для пространственного случая аналогичны плоскому случаю (пункт 3.5).

Пусть в пространстве заданы две декартовы прямоугольные системы координат: "старая" с началом в точке и осями , , и "новая" с началом в точке и осями , , , причем оси одной системы координат соответствено параллельны осям другой системы и одинаково с ними направлены. Будем говорить, что вторая система координат получена из первой параллельным переносом.

Пусть начало новой системы координат имеет в старой системе координаты . Пусть  -- некоторая точка пространства с координатами в старой системе координат и  -- в новой системе координат. Тогда связь между "старыми" и "новыми" координатами точки задается формулами, аналогичными формулам (12.11):

(13.21)

Справедливо и предложение, аналогичное предложению 12.7.

        Предложение 13.1   Пусть некоторая поверхность задана уравнением

Тогда в системе координат с началом в точке и осями , , , полученной параллельным переносом, уравнение поверхности будет иметь вид .    

        Пример 13.2   Нарисуйте поверхность .

Решение. Выделим полные квадраты по переменным , и (см. пример 12.1):

Отсюда

Разделим обе части на 4:

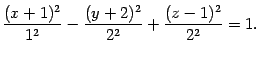
Введем новую систему координат с началом в точке , получающуюся из старой параллельным переносом. По предложению 13.1 получим, что в новой системе поверхность задается уравнением

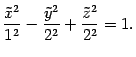
Данное уравнение отличается от канонического уравнения однополостного гиперболоида тем, что поменялись ролями оси ординат ( ) и аппликат ( ). Не переобозначая осей, произведем построение поверхности с помощью сечений. В сечении плоскостью получаем эллипс с уравнением

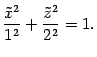
Его полуоси равны 1 и 2 и лежат соответственно на осях и . В сечении плоскостью получаем гиперболу с уравнением

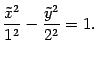
Ее мнимая ось лежит на оси , а действительная ось лежит на оси , полуоси соответственно равны 2 и 1. В сечении плоскостью получаем равностороннюю гиперболу с уравнением

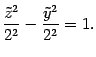
Ее мнимая ось лежит на оси , а действительная ось лежит на оси , обе полуоси равны 2. Для большей наглядности нарисуем еще два сечения плоскостями параллельными плоскости . В сечениях получим эллипсы, подобные эллипсу в плоскости . По рассмотренным сечениям можно представить себе форму гиперболоида и его расположение в пространстве (рис. 13.33). Объемное изображение приведено на рис. 13.34.

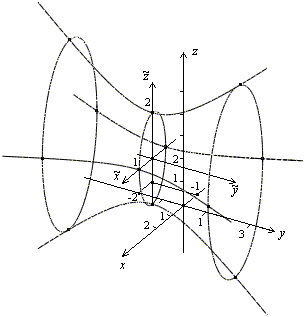
Рис.13.33.Изображение поверхности с помощью сечений

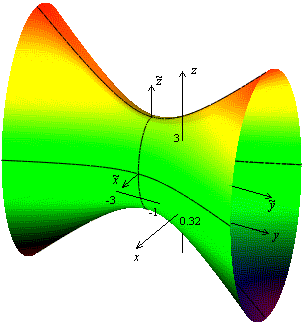
Рис.13.34.Объемное изображение поверхности

Основой для решения экономических задач являются математические модели.