71. Выборка. Репрезентативность выборки.

Выборочной совокупностью (выборкой) называется совокупность объектов, отобранных случайным образом из генеральной совокупности.

Выборка – это последовательность X₁,X₂,…,X_n независимых одинаково распределенных случайных величин, распределение каждой из которых совпадает с распределением генеральной случайной величины.

Число объектов (наблюдений) в совокупности называется её объемом.

Конкретные значения выборки, полученные в результате наблюдений (испытаний), называются реализацией выборки.

Метод статистического исследования, состоящий в том, что на основе изучения выборочной совокупности делается о всей генеральной совокупности, называется выборочным.

Для получения хороших оценок характеристик генеральной совокупности необходимо, чтобы выборка была репрезентативной (или представительной), т.е. достаточно полно представлять изучаемые признаки генеральной совокупности. Условием обеспечения репрезентативности выборки является, согласно закону больших чисел, соблюдение случайности отбора, т.е. все объекты генеральной совокупности должны иметь равные вероятности попасть в выборку.

№72. Чисельні характеристики вибірки. Їх звязок з чисельними характеристиками генеральної сукупності.

Для характеристики варіаційного ряду (вибірки) застосовують наступні величини:

1) Вибіркове середнє : , .

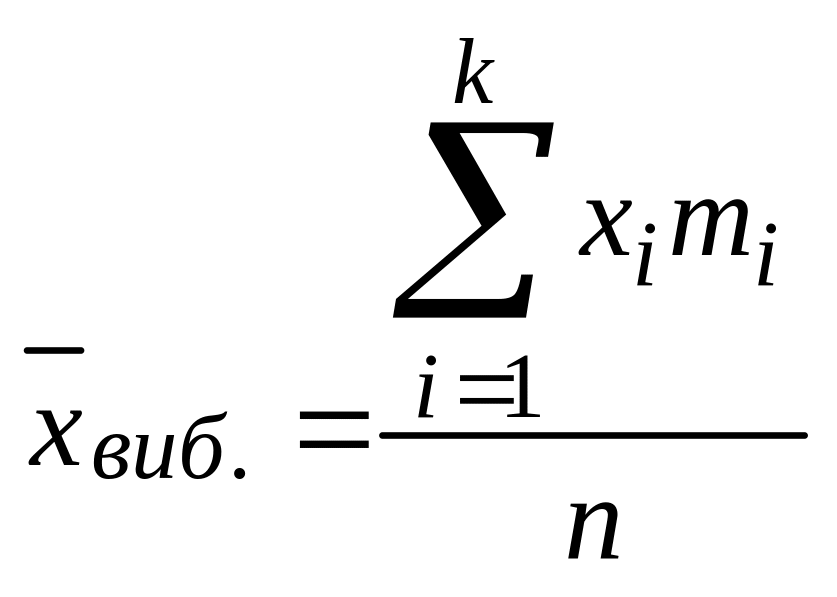2) Вибіркова дисперсія : , або .

3) Вибіркове середнє квадратичне відхилення : = .

4) Коефіцієнт варіації: .

5) Початкові моменти k-го порядку: .

6) Центральні моменти k-го порядку:

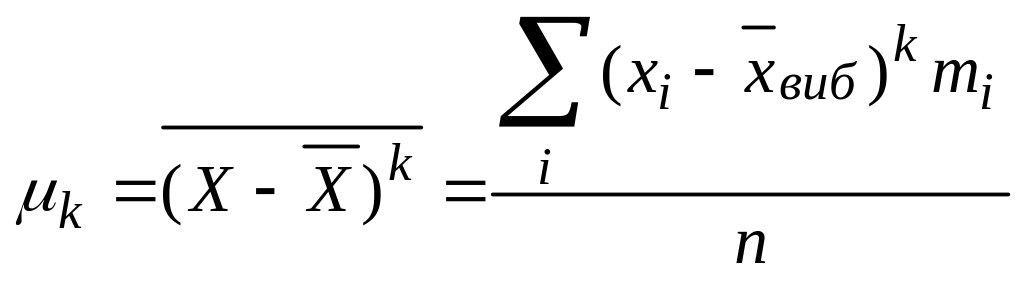
7) Асиметрія: характеризує відхилення випадкової величини від свого центрального положення вліво або вправо.

8) Ексцес: . характеризує відхилення випадкової величини від свого центральногоположення вгору або вниз.

9) Мода - це варіанта з максимальною частотою, тобто: .

10) Медіана - це варіанта, яка поділяє варіаційний ряд на дві рівні за числом елементів частини. Звязок між характеристиками генеральної та вибіркової сукупностей. Груповою середноьою називають середнє арифметичне значень ознаки, які належать групі: . При наявності кількох вибірок у генеральній сукупності з груповими середніми , ,…, _{k виб} та обємами введемо термін загальної середноьї для всієї сукупності. Загальне середнє дорівнює середньому арифметичному групових середніх, зваженому за обємами груп: 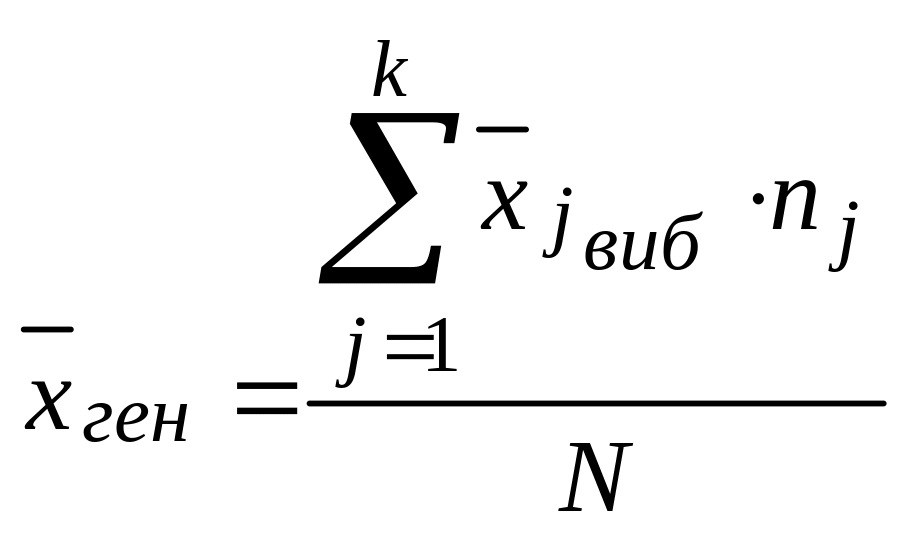, де j – номер групи, N - обєм всієї сукупності ( ). Для того, щоб охарактеризувати розсіяння значень ознаки Х генеральної сукупності навколо свого середнього значення, вводять генеральну дисперсію і генеральне середнє квадратичне відхилення за формулами: 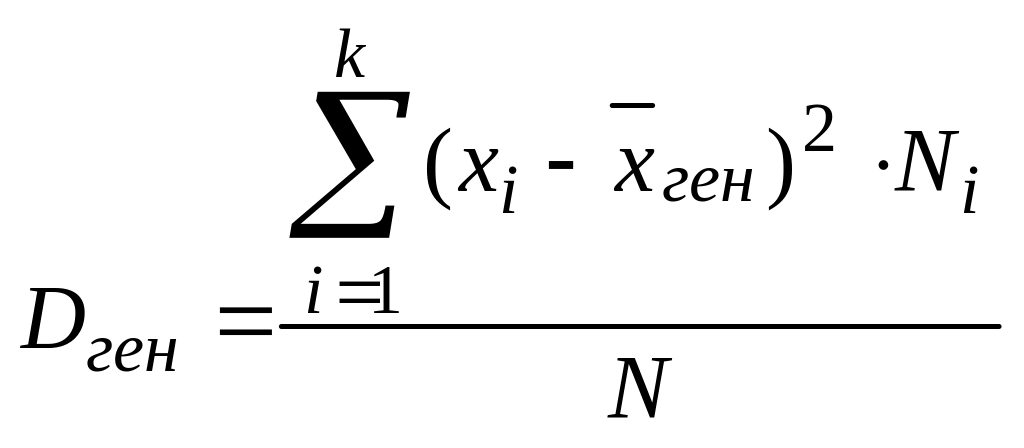, , де можливі значення ознаки мають відповідно частоти 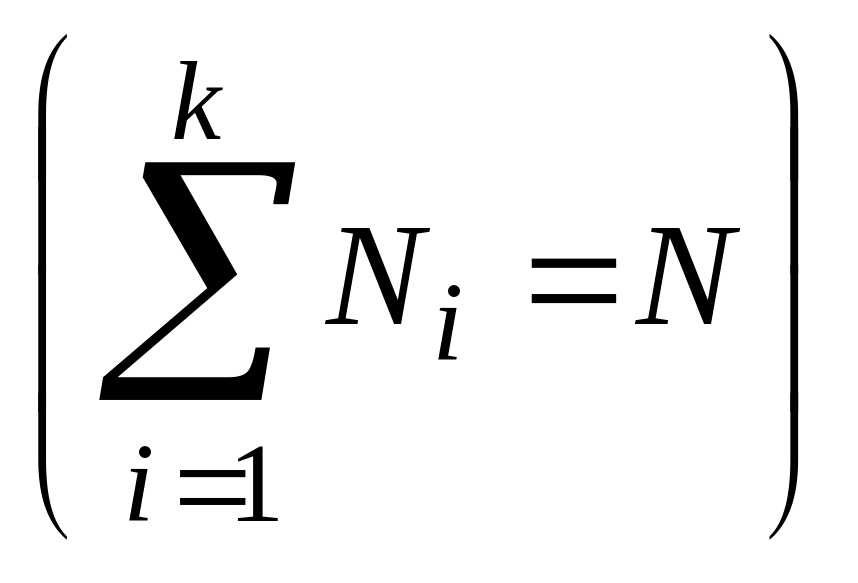. Для вибіркової дисперсії маємо формули: , або .

73. Точечные оценки выборки. Её свойства: несмещенность , состоятельность, эффективность.

Приближенное значение параметра генеральной совокупности, что вычисляется за выборкой, называется оценкой параметра. Как правило, основными оценками генеральной совокупности есть средние выборочное , которое аналогично математическому ожиданию М(Х), и выборочная дисперсия - аналог дисперсии D(X).

Допустим есть параметр  а ^* - его выборочная оценка. Для того, чтобы оценка ^* достаточно полностью характеризовала параметр генеральной совокупности, необходимо, чтоб она имела следующие свойства: несмещенность, состоятельность, эффективность.

Оценка ^* параметра  называется несмещенностью, если её математическое ожидание равно заданному параметру, то есть

М(^*)= (например  М( ))

Оценка называется состоятельной, если она при п следует за вероятностью к параметру, который оценивают, то есть

.

Оценка называется эффективной, если при заданном объеме исследований, она имеет наименьшую дисперсию.