- •Учебно-методический комплекс дисциплины математика
- •080801 «Прикладная информатика (в экономике)»
- •2. Распределение часов по формам учебных занятий (таблица с титульного листа рабочей программы)
- •3. Общие положения
- •3.1. Учебные и воспитательные задачи
- •3. 2. Формы и методы учебных занятий
- •3.3 Формы контроля знаний
- •Распределение часов по темам и видам учебных занятий (очная форма обучения)
- •Содержание лекционного курса
- •1 Семестр
- •2 Семестр
- •Тема 2. Дифференциальное исчисление, экстремумы функций
- •Тема 3. Интегральное исчисление
- •Тема 4. Дифференциальные уравнения
- •3 Семестр
- •4 Семестр
- •Тема 5. Целочисленное программирование
- •Тема 6. Элементы теории игр
- •Тема 7. Сетевые методы
- •Тема 8. Элементы динамического программирования
- •Тема 9. Элементы системы национальных счетов
- •Содержание семинарских, практических и лабораторных занятий
- •6. Рекомендации по выполнению курсовой работы/курсового проекта:
- •7. Рекомендации по выполнению аудиторных и домашних контрольных работ для студентов всех форм обучения
- •8. Организация самостоятельной работы студентов (график срс)
- •9. Зачетные и экзаменационные вопросы
- •Третий семестр.
- •10. Рейтинговая система оценки знаний по математике
- •8.2 Шкала для оценки знаний студентов по дисциплине
- •11. Список литературы
- •Действия над матрицами
- •Умножение матрицы на число.
- •Сложение матриц.
- •Умножение матриц.
- •Определители матриц второго и третьего порядка
- •Свойства определителей го порядка
- •Обратная матрица
- •Ранг матрицы
- •Формула Крамера
- •Метод Гаусса
- •Комплексные числа Алгебраическая форма комплексного числа
- •Тригонометрическая форма комплексного числа
- •Показательная форма комплексного числа
- •2. Аналитическая геметрия Векторы. Основные понятия
- •Линейные операции над векторами
- •Скалярное произведение векторов и его свойства
- •Векторное произведение векторов и его свойства
- •Смешанное произведение векторов и его свойства
- •Прямая на плоскости
- •Плоскость
- •Прямая в пространстве
- •Прямая и плоскость в пространстве
- •Кривые второго порядка
- •3.Теория пределов Предел последовательности
- •Основные теоремы о пределах
- •Предел функции
- •Основные теоремы о пределах
- •Замечательные пределы
- •Классификация точек разрыва:
- •4. Производная
- •Правила дифференцирования
- •Способы нахождения производной
- •Производные высших порядков
- •Применение производной при исследовании функций Максимум и минимум функции
- •Алгоритм нахождения наибольшего и наименьшего значения функции на отрезке
- •Направление выпуклости. Точки перегиба
- •Асимптоты
- •Построение графиков функции
- •Применение производной при вычислении пределов
- •5. Неопределённый интеграл
- •Свойства неопределенного интеграла
- •Правила вычисления интегралов
- •Методы интегрирования Метод непосредственного интегрирования
- •Метод замены переменной и внесение под знак дифференциала
- •Метод интегрирования по частям
- •Интегрирование рациональных дробей
- •Интегралы от тригонометрических функций
- •Интегрирование некоторых иррациональных функций с помощью тригонометрических подстановок
- •6. Определённый интеграл
- •Основные свойства определенного интеграла
- •Замена переменной в определенном интеграле
- •Приложения определенного интеграла Вычисление площади
- •Вычисление длины дуги кривой
- •7. Дифференциальные уравнения
- •Однородные уравнения
- •Линейные уравнения
- •Уравнение Бернулли
- •Уравнение в полных дифференциалах
- •Линейные дифференциальные уравнения с постоянными коэффициентами
- •Линейные однородные дифференциальные уравнения
- •Линейные неоднородные дифференциальные уравнения
- •8. Ряды
- •Свойства сходящихся рядов
- •Достаточные признаки сходимости знакоположительных рядов
- •Знакопеременные ряды
- •Свойства абсолютно и условно сходящихся рядов
- •Функциональные ряды
- •Степенные ряды
- •Ряды Тейлора и Маклорена
- •Разложение некоторых элементарных функций в ряд Маклорена
- •Вариант 1
- •Вариант 2
Интегрирование рациональных дробей
Определение.
Функция
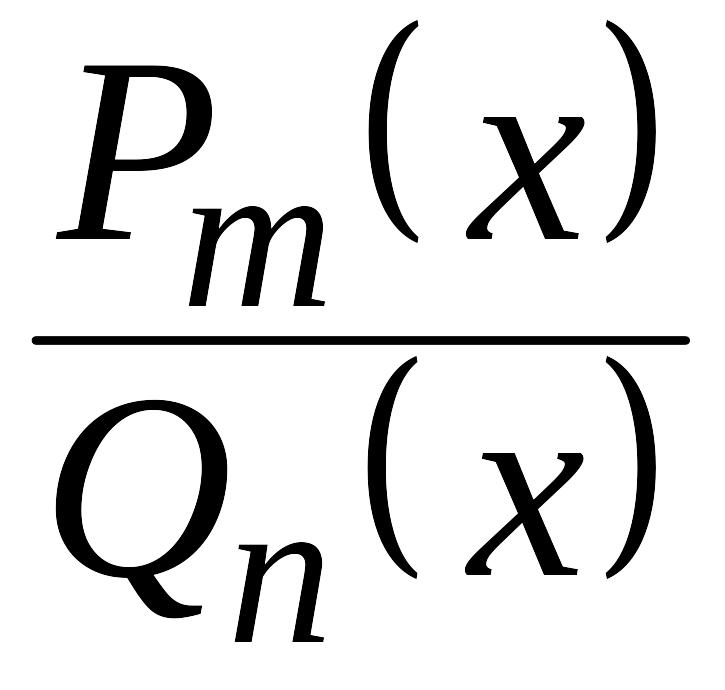 ,
где
,
где
![]() и
и
![]() являются многочленами, называется
дробно-рациональной
(или просто рациональной дробью). Если
степень числителя меньше степени
знаменателя, то дробь называется
правильной,
в противном случае – неправильной.
являются многочленами, называется
дробно-рациональной
(или просто рациональной дробью). Если
степень числителя меньше степени
знаменателя, то дробь называется
правильной,
в противном случае – неправильной.
Примеры
правильных рациональных дробей:
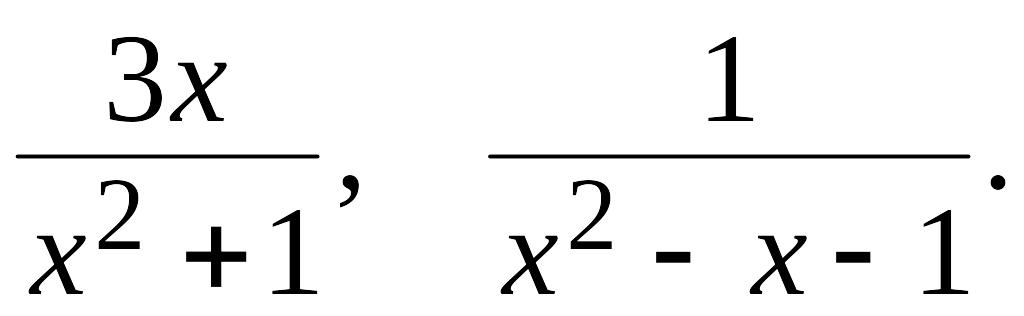
Примеры
неправильных рациональных дробей:
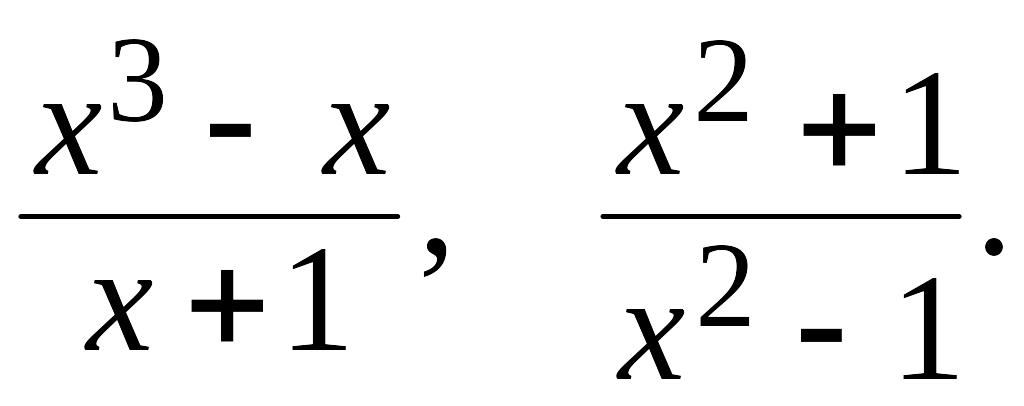
Если рациональная дробь неправильная, то ее можно представить в виде суммы некоторой целой части и правильной рациональной дроби.
Рассмотрим
пример такой процедуры для дроби
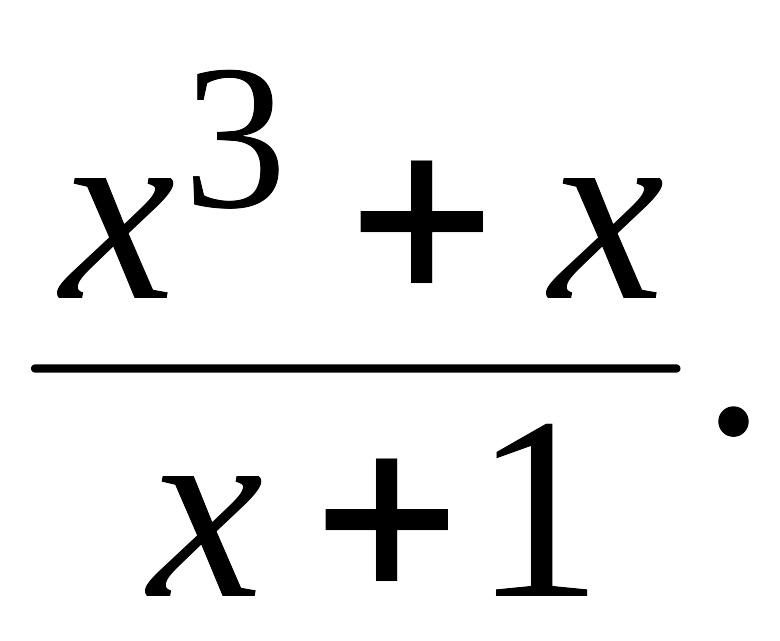
Процесс выделения целой части для данной неправильной рациональной дроби напоминает процедуру деления чисел уголком:
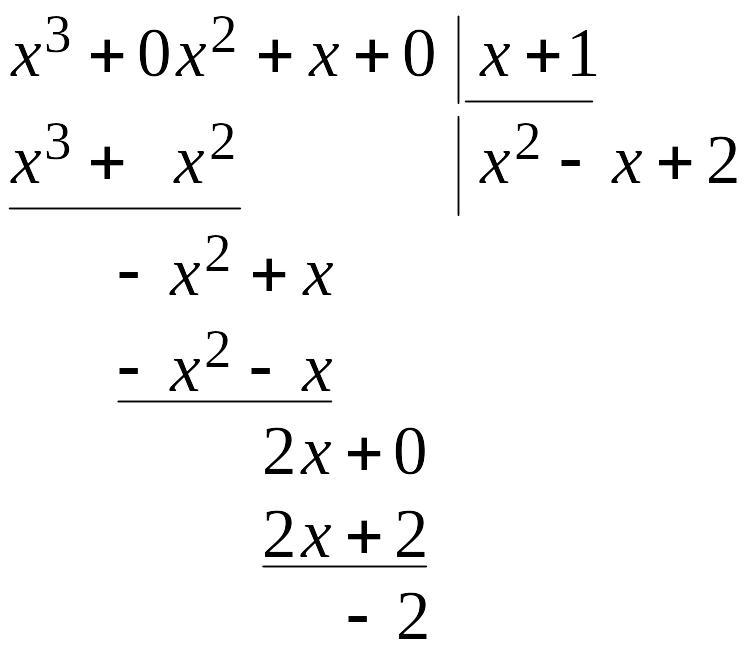
Таким
образом:
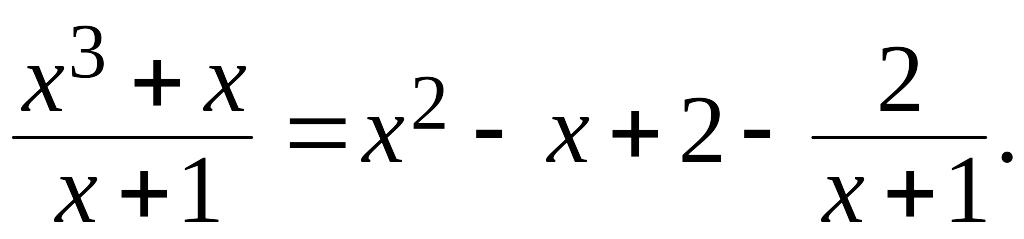
Определение. Правильные рациональные дроби вида:
I.
![]() III.
III.
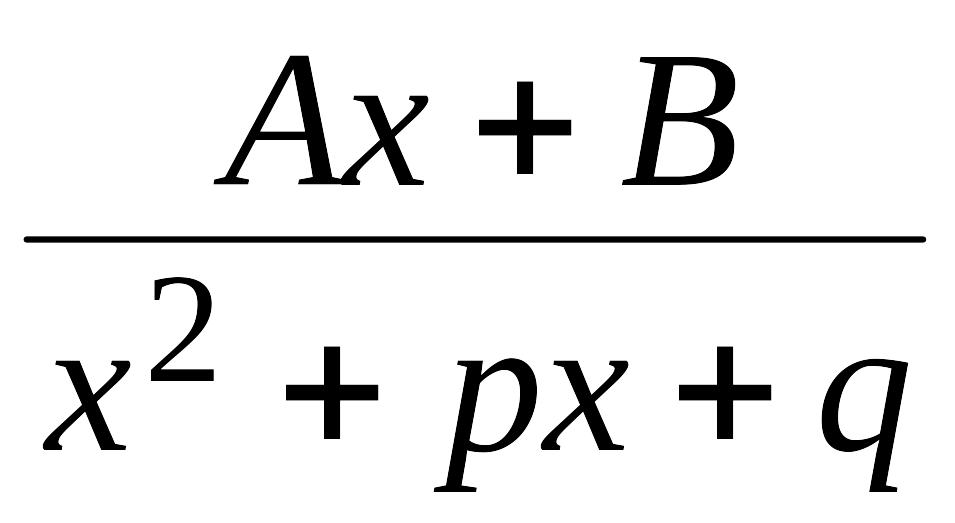 ,
где
,
где
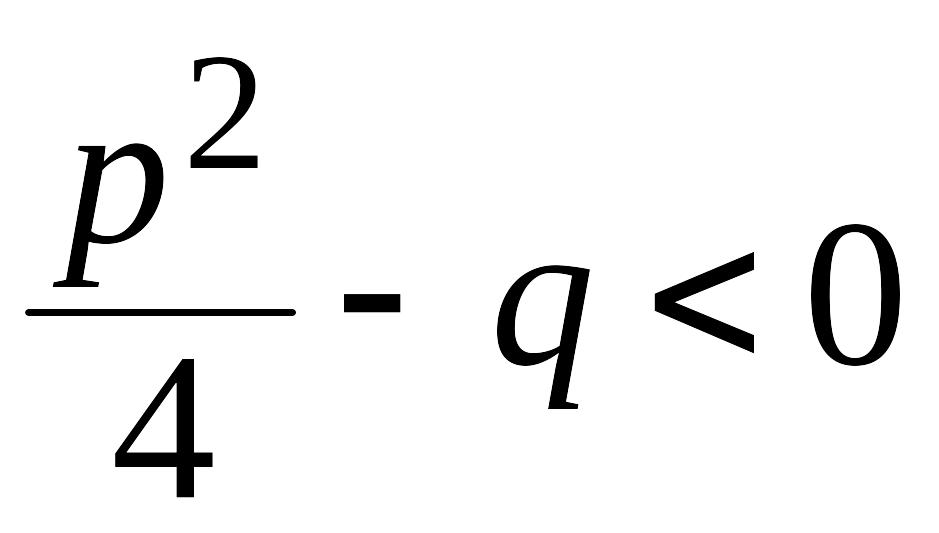
II.
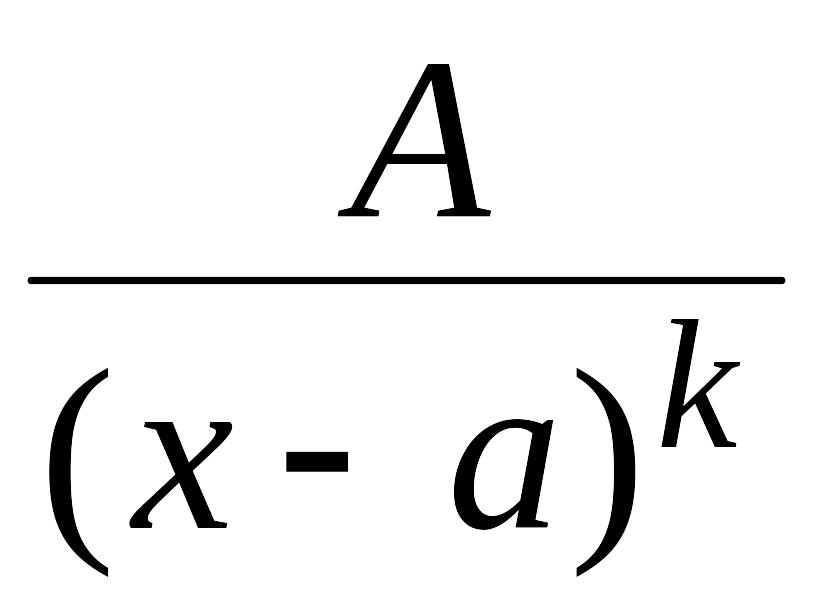 IV.
IV.
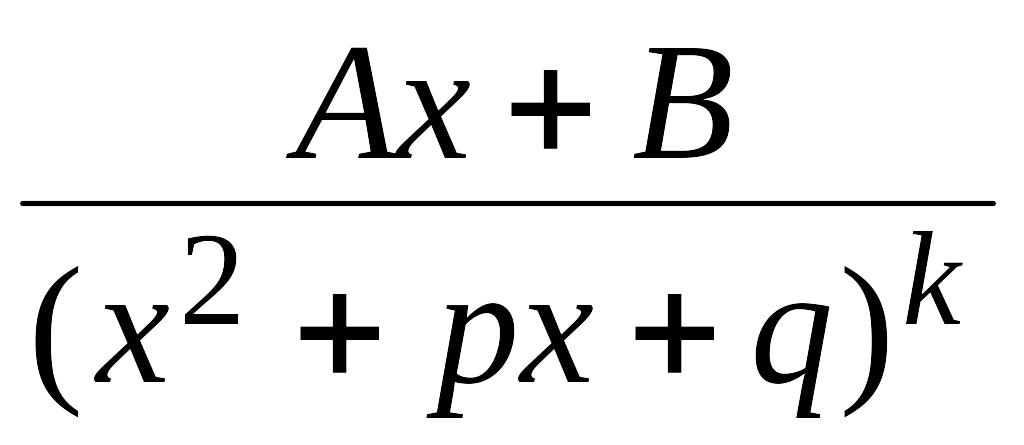 ,
где
,
где
![]()
называются простейшими дробями соответственно I, II, III и IV типов.
Интегралы от дробей I и II типа являются табличными. Интеграл от дроби III типа требует тождественных преобразований, связанных с выделением полного квадрата в знаменателе дроби и приведение исходной дроби к табличным интегралам. Осуществляется это следующим образом (выкладки проделаны в общем виде):
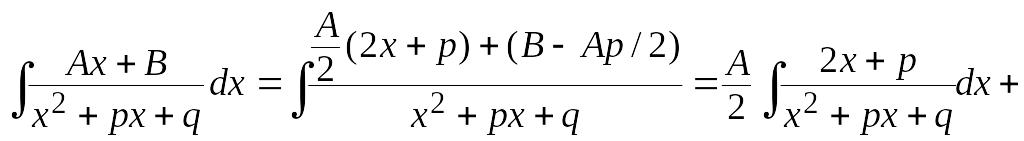
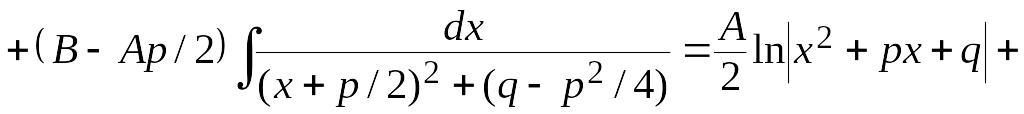
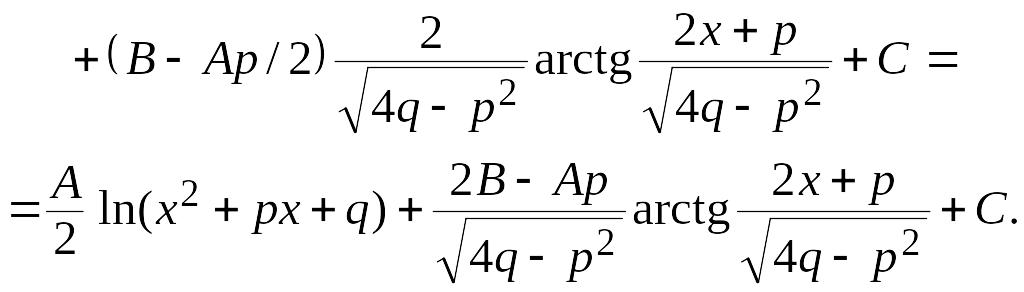
Интегрирование дроби IV типа приводит к более сложным вычислениям. Поэтому этот случай не рассматриваем, а в случае необходимости рекомендуем изучить литературу, приведенную в конце данного пособия.
Всякая правильная рациональная дробь может быть представлена в виде суммы дробей простейшего типа I-IV. Это позволяют сделать следующие теоремы:
Теорема.
Если
![]() является действительным корнем кратности
k
для знаменателя правильной рациональной
дроби
является действительным корнем кратности
k
для знаменателя правильной рациональной
дроби
![]() ,
то последнюю можно представить в виде
суммы двух правильных рациональных
дробей:
,
то последнюю можно представить в виде
суммы двух правильных рациональных
дробей:
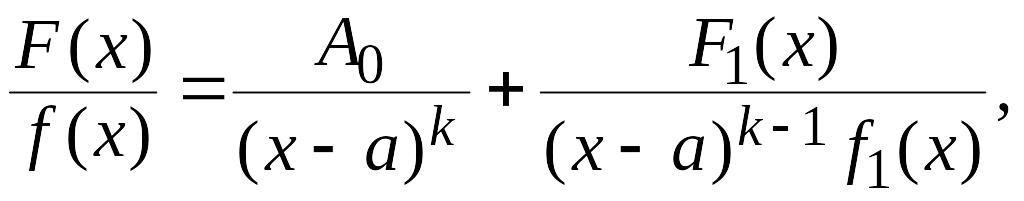 где
где
![]() ,
а степень многочлена
ниже степени знаменателя
,
а степень многочлена
ниже степени знаменателя
![]()
Замечание.
К правильной рациональной дроби
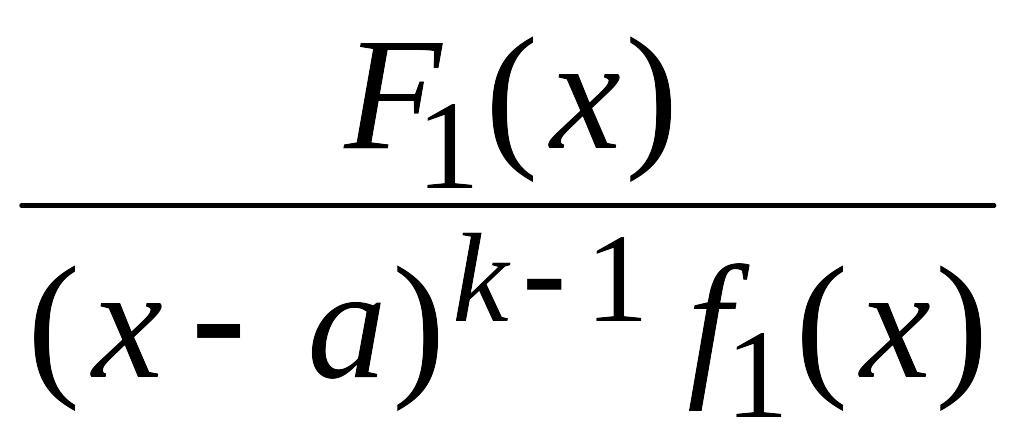 можно повторно применить данную теорему.
можно повторно применить данную теорему.
В конечном итоге, после многократного применения данной теоремы, исходная дробь допускает разложение:
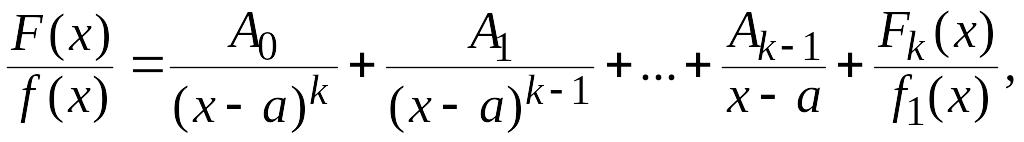
при
этом
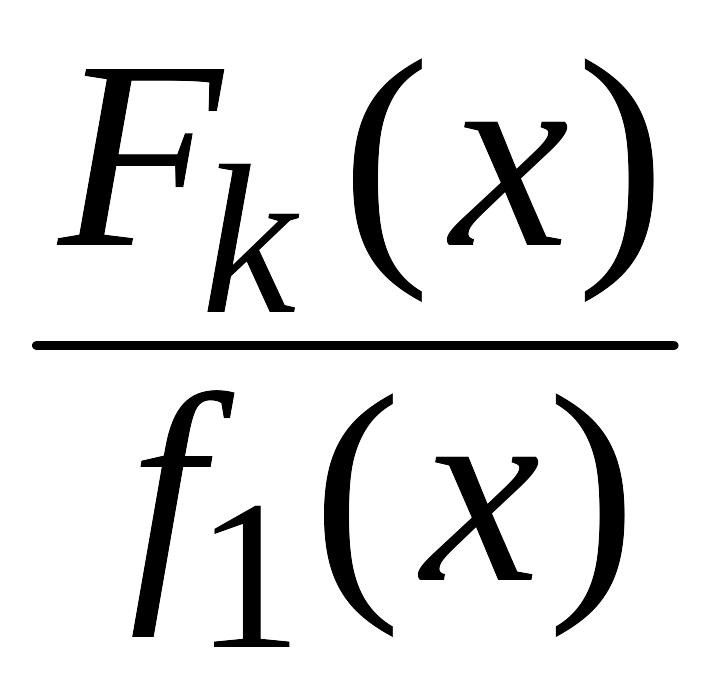 будет несократимой рациональной дробью.
будет несократимой рациональной дробью.
Теорема.
Если
![]() ,
где
,
многочлен
,
где
,
многочлен
![]() не делится на
не делится на
![]() ,
то правильную рациональную дробь
,
то правильную рациональную дробь
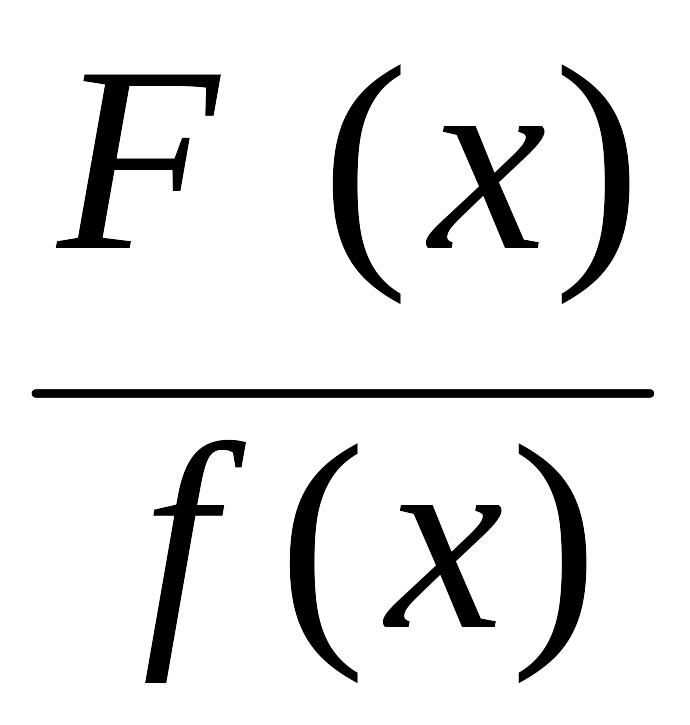 можно представить в виде суммы следующих
правильных дробей:
можно представить в виде суммы следующих
правильных дробей:
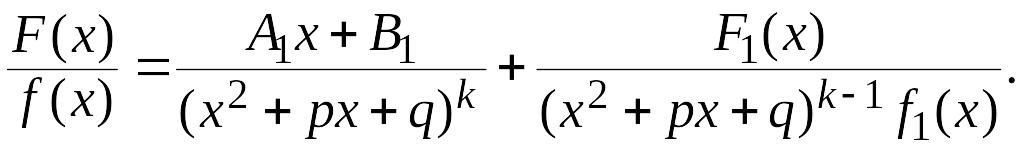
Замечание.
Применяя данную теорему к дроби
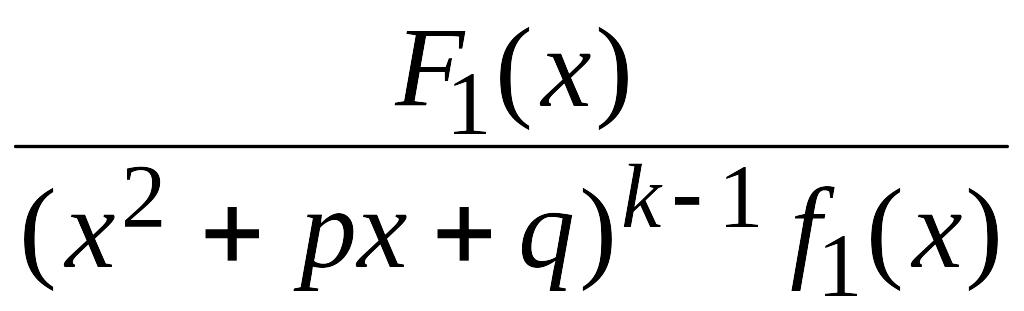 и, продолжая этот процесс для вновь
полученных дробей, в итоге получаем
разложение:
и, продолжая этот процесс для вновь
полученных дробей, в итоге получаем
разложение:
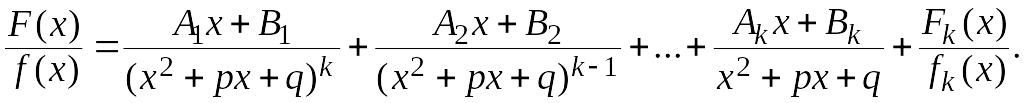
Коэффициенты
![]() в разложениях, как в случае действительных
корней, так и в случае комплексных
корней, можно найти с помощью метода
неопределенных коэффициентов. Суть
этого метода рассмотрим на конкретных
примерах.
в разложениях, как в случае действительных
корней, так и в случае комплексных
корней, можно найти с помощью метода
неопределенных коэффициентов. Суть
этого метода рассмотрим на конкретных
примерах.
Пример
8. Вычислить
интеграл
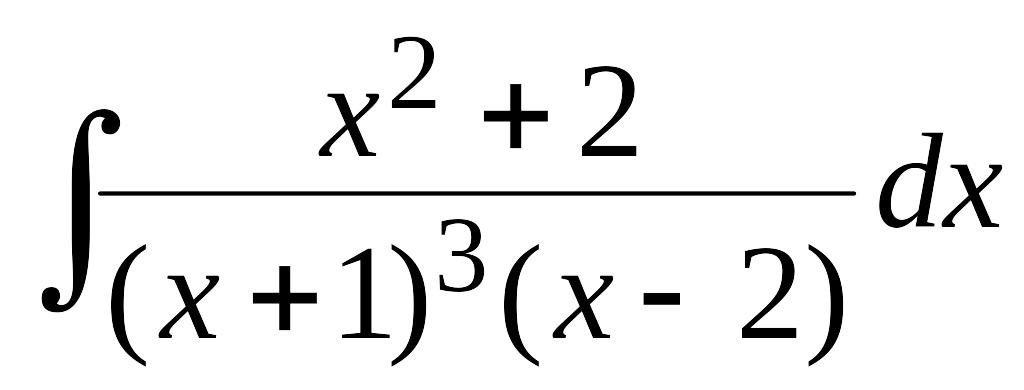
Решение.
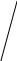
 Подынтегральная
функция представляет собой правильную
рациональную дробь, знаменатель которой
имеет корень
Подынтегральная
функция представляет собой правильную
рациональную дробь, знаменатель которой
имеет корень
![]() ,
кратность которого равна 3, и простой
корень
,
кратность которого равна 3, и простой
корень
![]() .
Следовательно, эта дробь на основании
приведенной выше теоремы может быть
представлена в виде суммы дробей I и II
типа:
.
Следовательно, эта дробь на основании
приведенной выше теоремы может быть
представлена в виде суммы дробей I и II
типа:
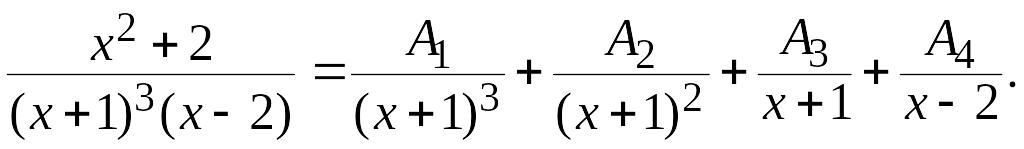
Приводя к общему знаменателю дроби в правой части последнего равенства и приравнивая числители, получим:
![]() ,
или
,
или
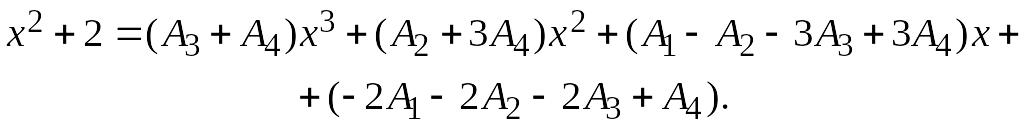
Приравнивая
коэффициенты при одинаковых степенях
переменных, получаем систему уравнений
для
![]() :
:
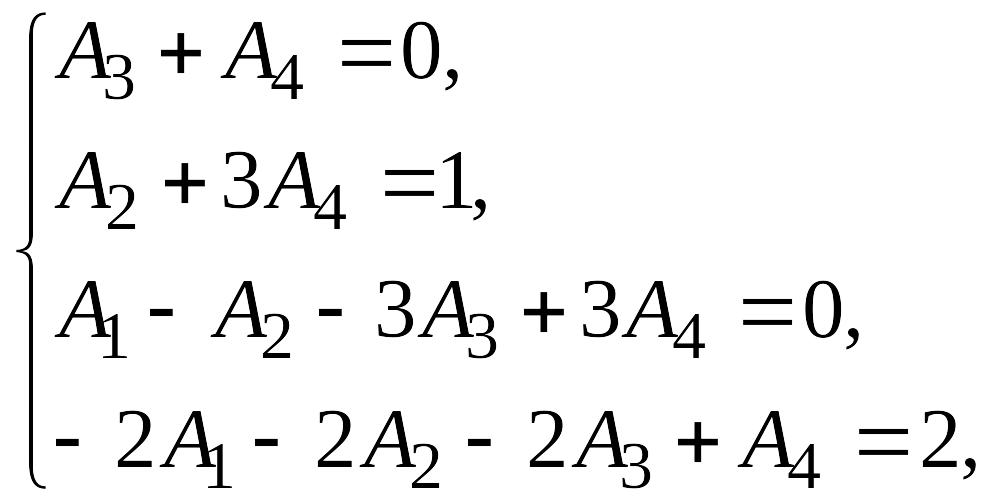
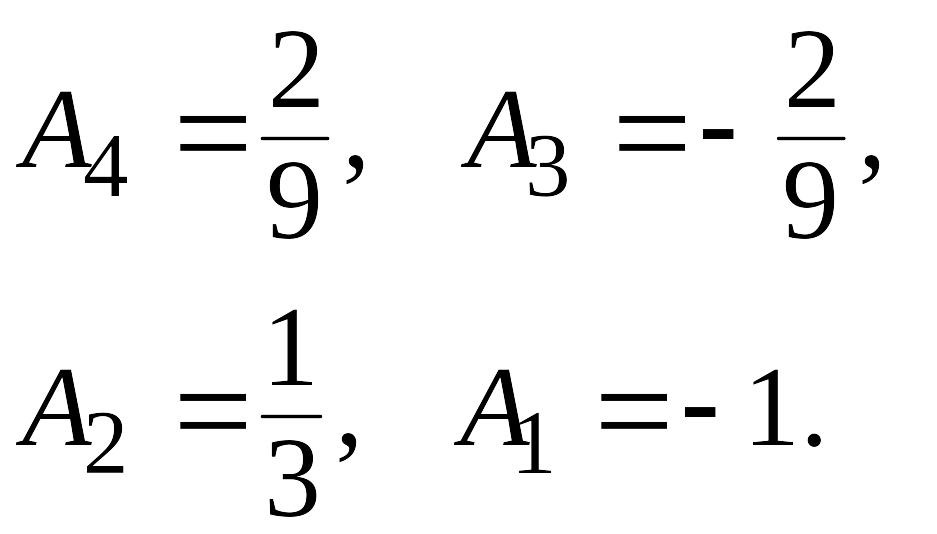
Исходный интеграл может быть представлен:
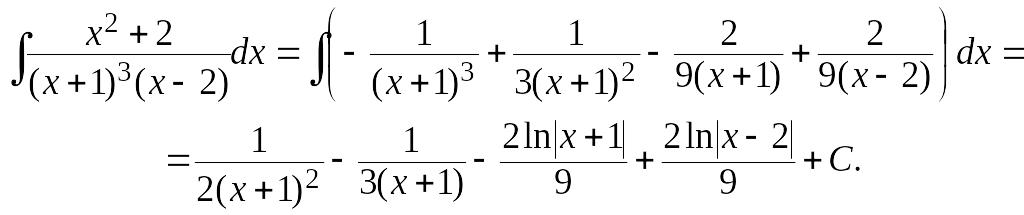
Пример
9. Вычислить
интеграл:
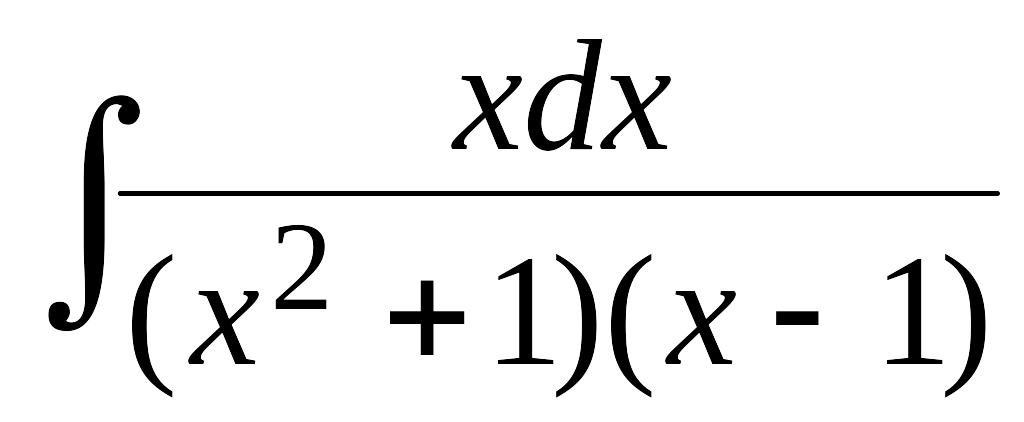
Решение.
Разложим подынтегральную функцию на
дроби простейшего типа I
и III,
так как в знаменателе корень:
![]() − простой действительный, а уравнение
− простой действительный, а уравнение
![]() имеет простые комплексные корни.
имеет простые комплексные корни.
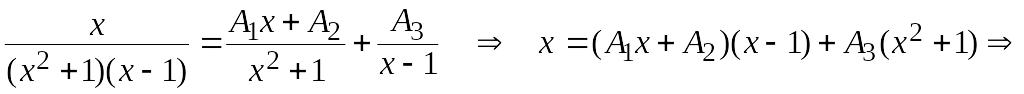
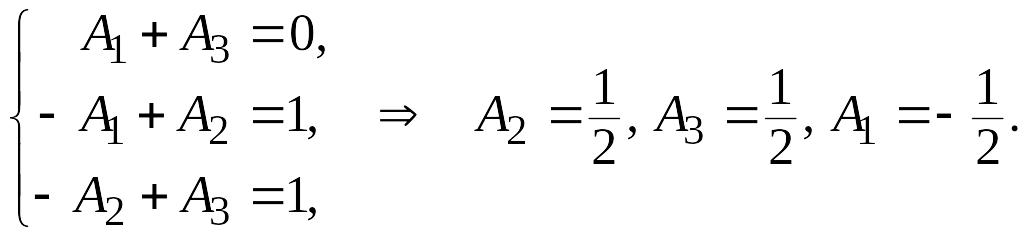
Таким образом: