Векторное произведение векторов и его свойства

Определение. Три некомпланарных вектора , взятые в указанном порядке, образуют правую тройку, если с конца третьего вектора кратчайший поворот от первого вектора ко второму вектору виден совершающимся против часовой стрелки, и левую, если по часовой стрелке.

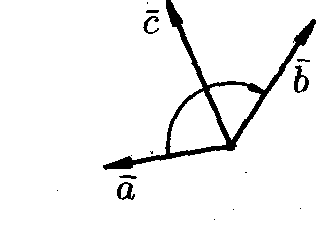
правая тройка

левая тройка

Определение. Векторным произведением вектора на вектор называется вектор , который:

1. перпендикулярен векторам и , т.е. 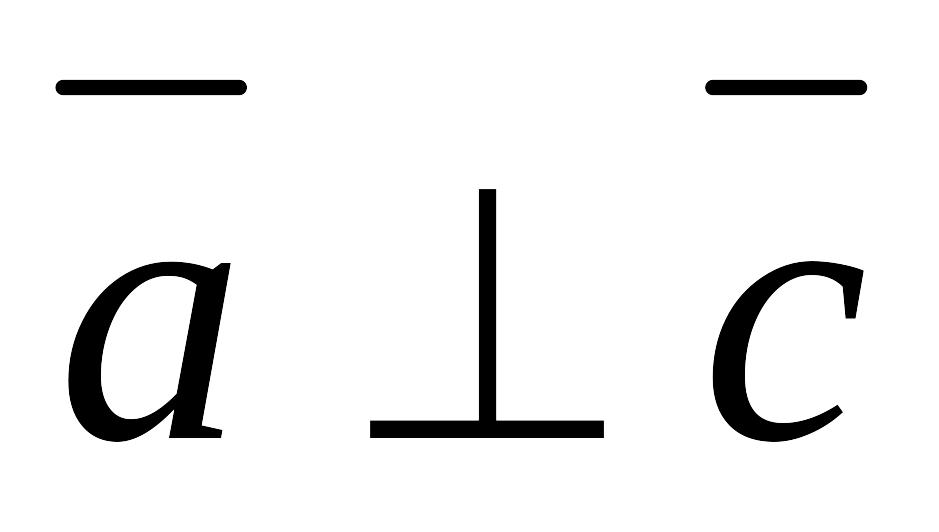и ;

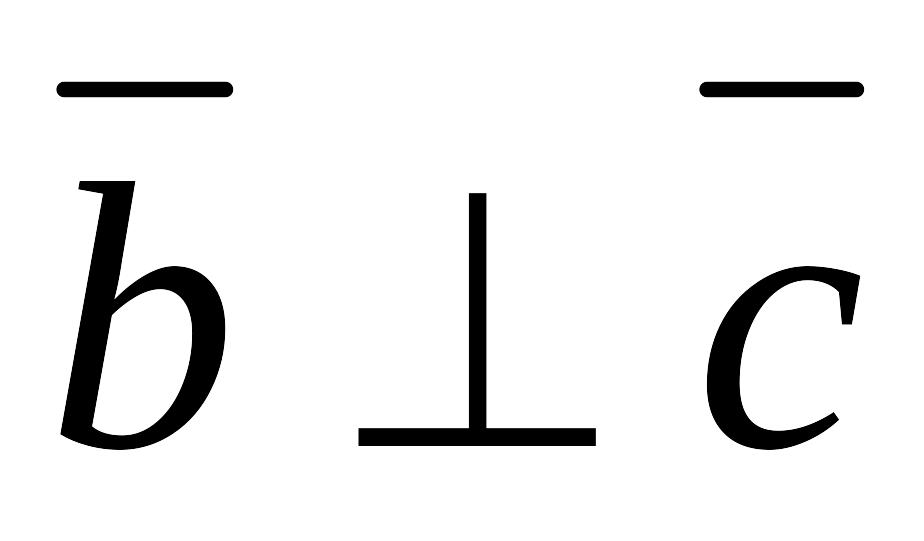2. имеет длину, численно равную площади параллелограмма, построенного на векторах и как на сторонах, т.е.

, где ;

3. 

   

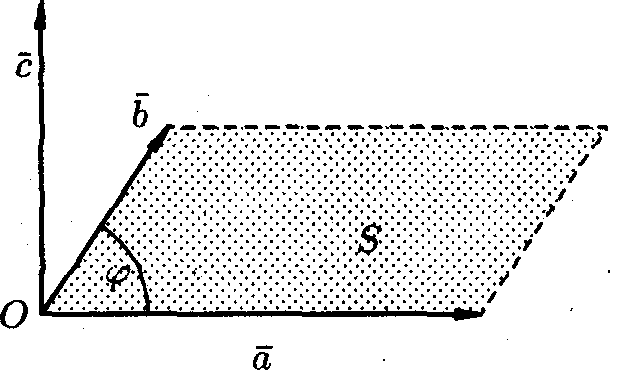
   векторы образуют правую тройку.

Векторное произведение обозначается . Из определения векторного произведения непосредственно вытекают следующие соотношения между ортами , которые образуют правую тройку:

Векторное произведение обладает следующими свойствами:

1. При перестановке сомножителей векторное произведение меняет знак, т.е.

.

2. Сочетательное свойство:

;

3. Распределительное свойство:

;

.

4. Два ненулевых вектора и коллинеарны тогда и только тогда,

когда их векторное произведение равно нулевому вектору, т.е.

.

Выражение векторного произведения через координаты векторов и :

.

Смешанное произведение векторов и его свойства

Определение. Смешанным произведением векторов , и называется скалярное произведение векторного векторов и на вектор .

Смешанное произведение обозначают и по определению

= .

Результатом смешанного произведения является скалярная величина.

Теорема. Смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах; взятому со знаком «плюс», если эти векторы образуют правую тройку, и со знаком «минус», если эти векторы образуют левую тройку.

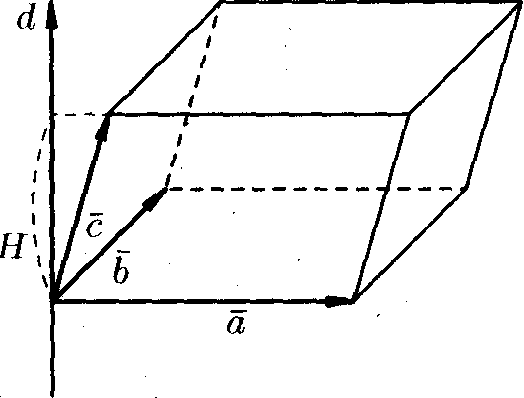
Смешанное произведение обладает следующими свойствами:

1. смешанное произведение не меняется при циклической перестановке сомножителей, т.е.

2. Смешанное произведение не меняется при перемене местами знаков векторного и скалярного умножения, т.е.

.

3. Смешанное произведение меняет свой знак при перемене мест любых двух векторов-сомножителей, т.е.

4. Смешанное произведение ненулевых векторов , и равно нулю тогда и только тогда, когда они компланарны.

Теорема. Смешанное произведение равно определителю третьего порядка, составленному из координат перемножаемых векторов, т.е.

.

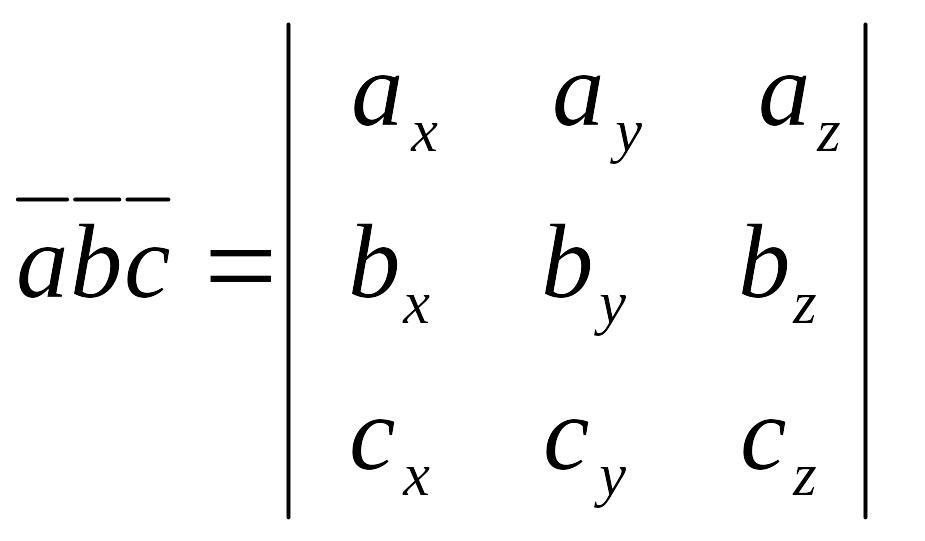Таким образом, объем параллелепипеда, построенного на векторах , и вычисляется как

,

а объем треугольной пирамиды, построенной на этих же векторах, равен

Пример1. Вершинами пирамиды служат точки и . Найти объем пирамиды.

Решение.

Находим векторы , и .:

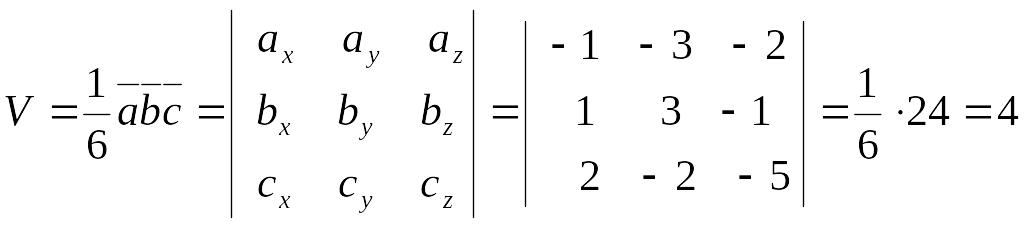куб.ед.

Прямая на плоскости

Уравнение прямой, проходящей через точку перпендикулярно вектору = , получают на основе использования скалярного произведения двух векторов.

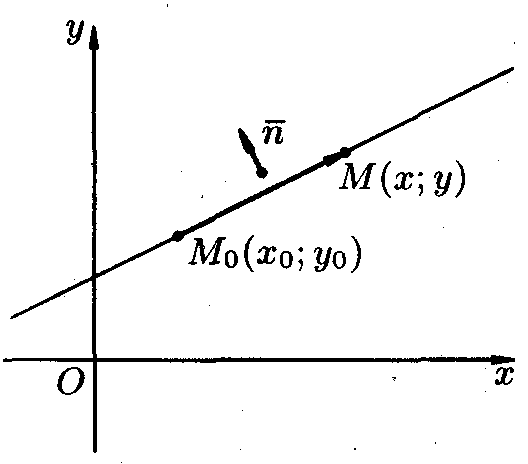
Пусть – произвольная точка прямой .

Определение. Вектор = перпендикулярный прямой называется нормальным вектором прямой .

Тогда и по условию перпендикулярности векторов

Если в уравнении раскрыть скобки, то получится общее уравнение прямой

где

Если , то из общего уравнения прямой получаем

или

уравнение прямой с угловым коэффициентом, где ,

Обозначим угол между положительным направление оси ОХ и заданной прямой . Тогда называется угловым коэффициентом данной прямой. Число - ордината точки пересечения прямой с осью Оу.

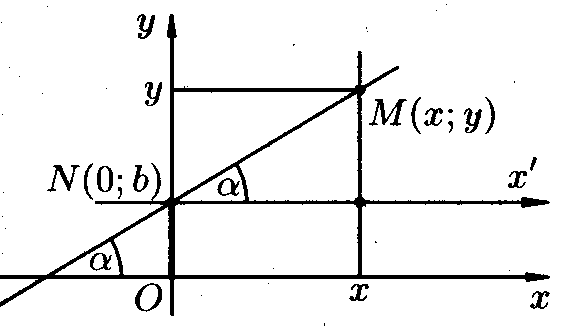
Рассмотрим угловой коэффициент и произвольную точку . Определение. Уравнение прямой представленное в виде

называют уравнением прямой проходящей чрез заданную точку с заданным угловым коэффициентом.

Определение. Уравнение, имеющее вид

,

Называют каноническим уравнением прямой (уравнение прямой, проходящей через две заданные точки) .

Или через определитель

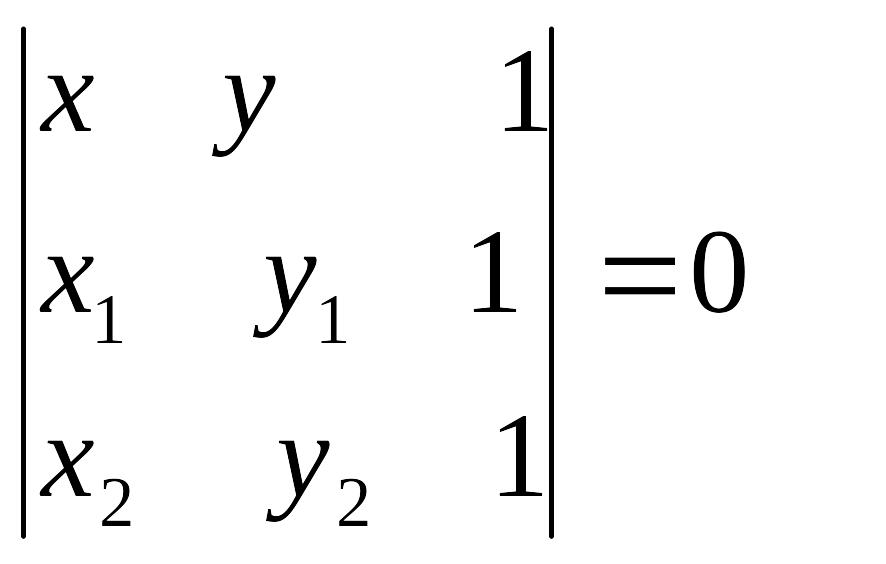
Определение. Уравнение, имеющее вид

,

называется уравнением прямой в отрезках, где а и b координаты точек

М(а,0) и N (0,b), лежащие на осях координат.

.

Пусть две прямые и

пересекаются и - угол между этими прямыми, отсчитывается против часовой стрелки от прямой , до прямой . Тогда угол определяется из соотношения:

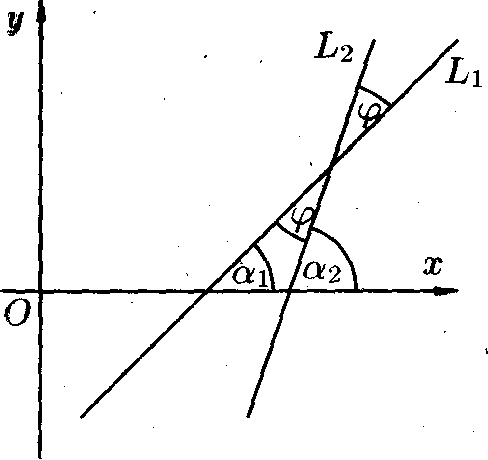
Если прямые и заданы общими уравнениями, т.е.

и ,

то угол между ними находится по формуле

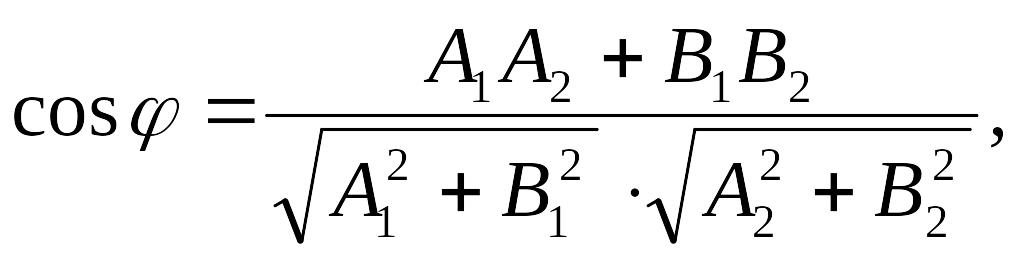
Условие параллельности прямых и имеет вид

или .

Условие перпендикулярности прямых и записывается в виде

или .

Чтобы найти точку пересечения непараллельных прямых и необходимо решить систему уравнений

.

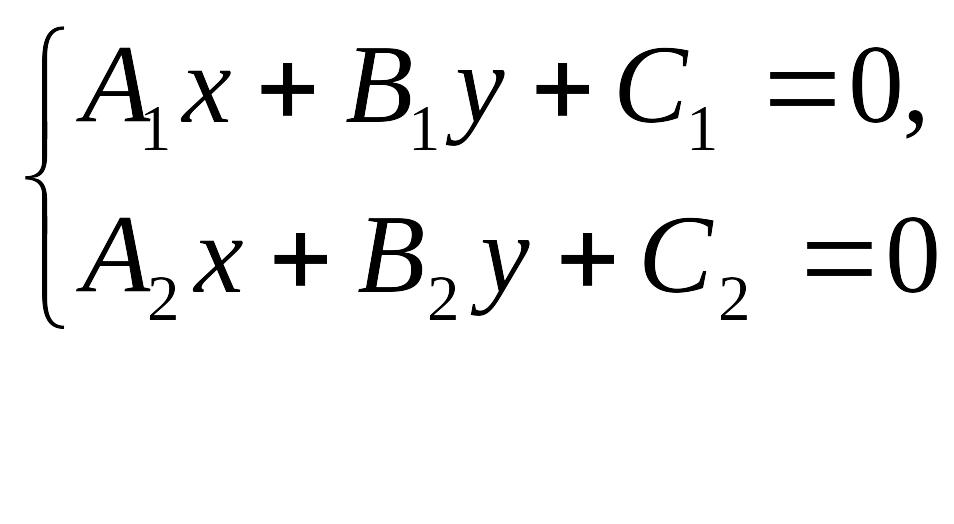Если три прямые пересекаются в одной точке, то

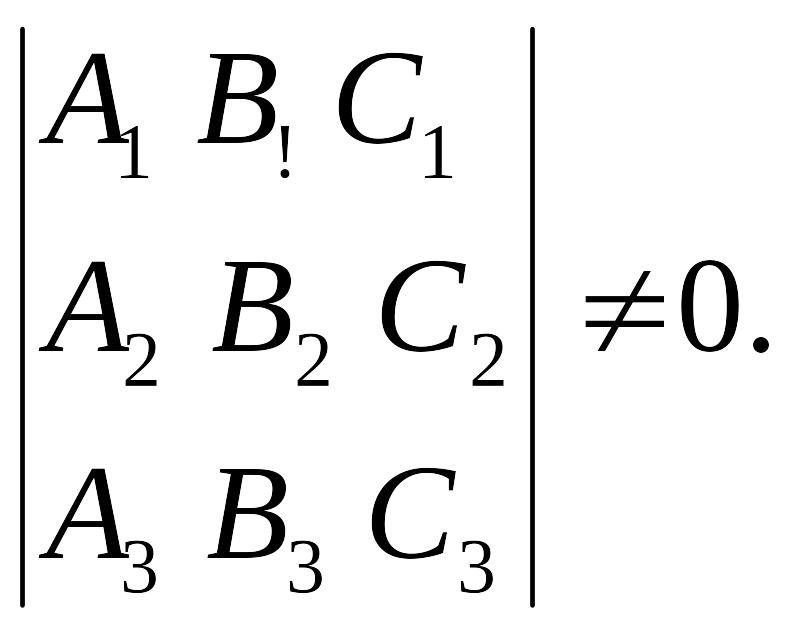
Расстояние от точки до прямой определяется по формуле

.

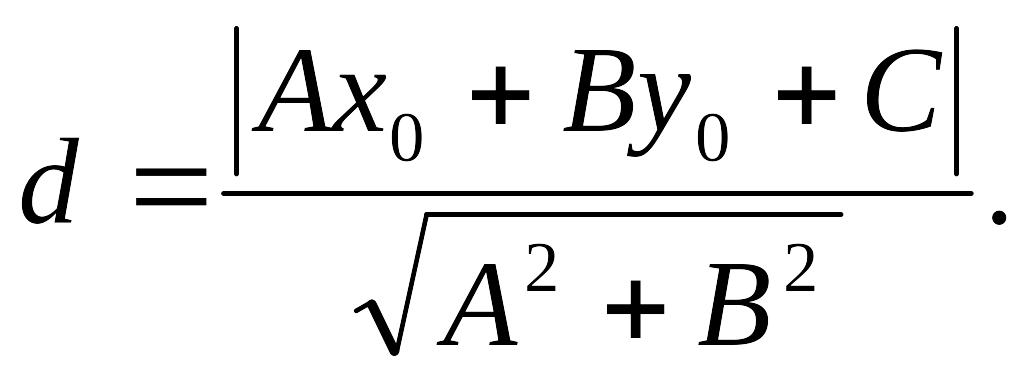Пример 1. Дано общее уравнение прямой . Написать: а) уравнение с угловым коэффициентом; б) уравнение в отрезках на осях.

Решение.

а)

б)

Пример 2. Определить угол между прямыми и

Решение.

Пример 3. Через точку М (5,2) провести прямую, перпендикулярную прямой

Решение.

Т.к. прямые перпендикулярны, то угловой коэффициент искомой прямой Подставляя в формулу уравнения прямой, проходящей через точку с заданным угловым коэффициентом, получим

Пример 4. Составить уравнение прямой, проходящей через точки (2,25) и (11,8).

Решение.

Воспользуемся уравнением прямой, проходящей через две точки: