Комплексные числа Алгебраическая форма комплексного числа

Определение. Комплексным числом называется выражение вида , где и - действительные числа, а - символ, который называют мнимой единицей.

Определение. Два комплексных числа и равны, если и .

Определение. Если , то комплексное число называется сопряженным для .

Действия над комплексными числами, записанными в алгебраической форме. Правила сложения, умножения и деления комплексных чисел:

1)

2)

3)

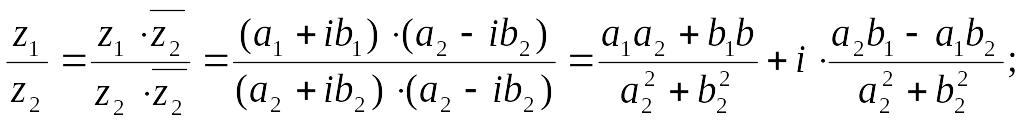
Тригонометрическая форма комплексного числа

Комплексное число можно изобразить точкой плоскости или ее радиусом-вектором . Длина вектора называется модулем комплексного числа и обозначается , т.е. , а угол между вектором и осью OX называется аргументом комплексного числа и обозначается через , т.е. .

Тогда

,

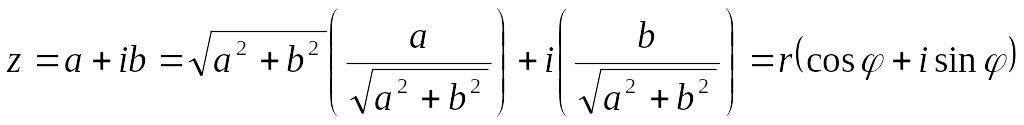где , а -решение системы

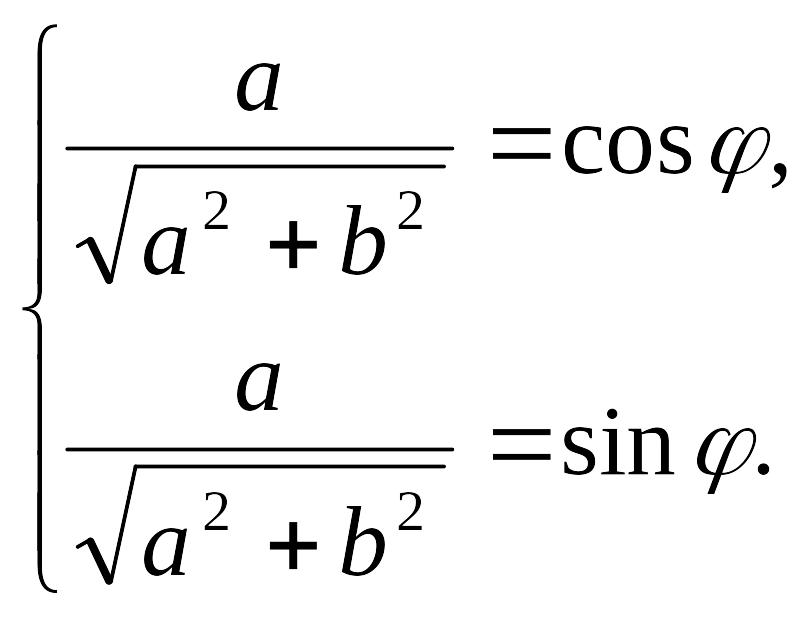
Действия над комплексными числами, записанными в тригонометрической форме. Правила умножения и деления комплексных чисел:

1)

2)

3)

Показательная форма комплексного числа

Действия над комплексными числами, записанными в показательной форме. Правила умножения, деления и возведения в степень комплексных чисел и :

1) 3)

2)

Пример 1..Даны комплексные числа , . Найти , , .

Решение. Используя формулы для алгебраической формы представления

,

.

(учли, что ).

,

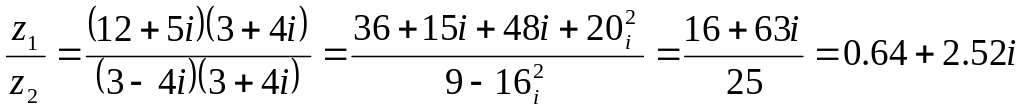Пример 2. Комплексные числа представить тригонометрической форме и найти z₁z₂ и z₁/z₂.

Решение. Используя тригонометрическую форму комплексного числа найдем модуль и аргумент комплексного числа : а из соотношения (1.11.5) получим аргумент числа z₁ (берем его главное значение): т.е.

Аналогичным образом для комплексного числа : т.е. и

Далее выполняем операции над комплексными числами в тригонометрической форме:

Пример 3. Найти (-1+i)²⁰.

Решение. В примере 2 мы получили, что Поэтому по формуле Муавра

= .

Пример 4. Записать комплексные числа в тригонометрической и показательной формах.

Решение: Согласно формулам комплексных чисел в показательной форме имеем

т.е.

Поэтому

Для z₂ имеем

т.е. Поэтому

2. Аналитическая геметрия Векторы. Основные понятия

Определение. Геометрическим вектором или просто вектором называется прямолинейный направленный отрезок.

Вектор обозначается двумя буквами , где первая буква указывает начало вектора, а вторая – его конец. Вектор может обозначаться и одной буквой латинского алфавита .

Определение. Расстояние между началом и концом вектора называется его длиной или модулем вектора и обозначают в виде

Определение. Вектор, длина которого равна нулю, называется нулевым вектором и обозначается . Нулевой вектор направления не имеет.

Определение. Вектор, длина которого равна единице, называется единичным вектором и обозначается .

Определение. Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными. Записывают

Коллинеарные векторы могут быть направлены одинаково или противоположно. Нулевой вектор считается коллинеарным любому вектору.

Определение. Два вектора называются равными ( ), если они коллинеарны, одинаково направлены и имеют одинаковые длины.

Определение. Три вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.