76. Узагальнений метод найменших квадратів. Визначення вектора і .

Умова гомоскедастичності є головною для лінійної класичної моделі і записується як

(10.5)

Для лінійних моделей з властивістю випадкового вектора , коли

(10.6)

(матриця є симетричною, додатньо визначеною матрицею n-го порядку) неможливим є використання звичайного МНК з метою визначення статистичних оцінок, як це було здійснено для лінійної класичної моделі. В такому випадку використовують так званий узагальнений метод найменьших квадратів (УМНК).

Нехай досліджується лінійна модель з порушення умови гомоскедастичності, а саме cov( Ω. Тоді додатно визначена матриця Ω допускає існування такої невиродженої матриці π, що Ω=π*π . Отже

π^-1*Ω(π^-1)’=I_n, oтже, Ω^-1=(π^-1)’* π^-1Враховуючи це для моделі , здійснивши перетворення отримаємо . Здійснивши перевірку моделі на наявність гетероскедастичності, маємо . Таким чином виявилося, що перетворена модель гетероскедастична і для неї можна використовувати такі самі формули що й для класичної лінійної моделі, а саме:

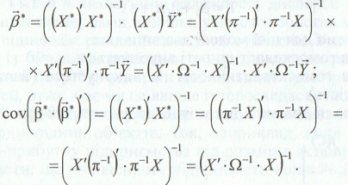
77. Зважений метод найменших квадратів. Визначення вектора і за умов а) та б) .

Методи усунення ознаки гетероскедастичності для лінійних моделей, що належать до парної регресії і які без зайвих ускладнень можуть бути використані і для множинних лінійних моделей.

1)

Нехай досліджується лінійна парна модель У векторно-матричній формі можна записати як де . Припустимо, що в моделі існує ознака гетероскедастичності з коваріаційною матрицею вектора , . Потрібно провести певні перетворення. Внаслідок них ми дістанемо модель , яку у веторно-матричній формі можна записати , де 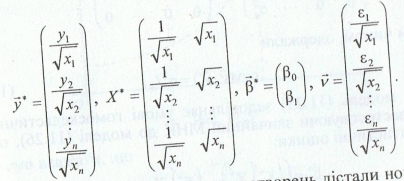. Перевіримо її на гетероскедастичність.

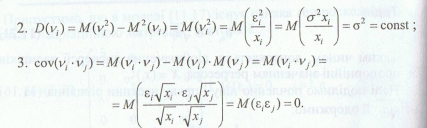.Тоді: . Застосовуючи МНК до моделі, отримаємо статистичні оцінки , визначивши цей емпіричний вектор, можемо сказати що

2) .

Тенденції зміни дисперсій випадкових залишків ε_і вектора грунтується на підставі розміщення точкок на координатній прощині. При розміщені цих точок в такому вигляді.

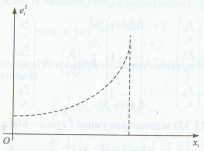можемо вважати, що або , де σ константа. Якщо кожен член рівняння поділимо на х_і, то Позначимо дістанемо або де 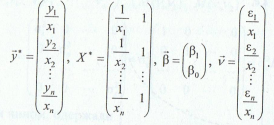Модель задовольняє умову Гаусса-Маркова 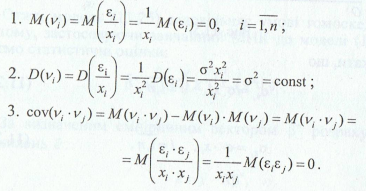Застосовуючи до моделі МНК, отримаємо із подальшим визначенням

78. Часовий ряд в загальному вигляді. Поняття тренду, сезонної, циклічної та випадкової компоненти. Основні етапи аналізу числових рядів?

Часовий ряд – це послідовність спостережень певної ознаки У у моменти часу t (t= ). Елементи цієї послідовності називають рівнями ряду і позначають y_t. В загальному вигляді їх можна представити таким чином:

y_t=u_t+ν_t+c_t+ε_t (t=1, 2, …,n)

u_{t –} тренд, плавно змінювана компонента, яка описує чистий вплив довготривалих факторів

ν_t – сезонна компонента, що уособлює вплив на У повторюваності економічних процесів протягом невеликих за своєю тривалістю періодів часу

c_t – циклічна компонента, яка визначає собою повторювальність економічних процесів протягом тривалих періодів часу.

ε_t – випадкова компонента, що визначає вплив множини факторів, які не підлягають врахуванню та реєстрації, внаслідок їх невизначеності.

Основні етапи аналізу числових рядів

1. Графічне зображення й опис поведінки часового ряду

2. Виділення невипадкових закономірних складових часового ряду

3. Вирівнювання й фільтрація

4. Дослідження випадкової складової ε_t часового ряду, побудова та перевірка на адекватність математичної моделі

5. Прогнозування розвитку досліджуваного економічного процесу за допомогою побудованого часового ряду

6. Дослідження взаємозв’язку між різними часовими рядами.