54. Етапи побудови економетричної моделі.

Економетричне моделювання базується на професійних знаннях про об'єкт дослідження і має такі етапи:

1. Знайомство з економічною теорією, визначення набору змінних, які описують процес функціонування досліджуваних об'єктів.

2. Аналіз взаємозв'язків між окремими змінними, висунення гіпотези взаємозв’язку. Залежні змінні називають ендогенними, а незалежні змінні - екзогенними.

3. Специфікація моделі. Прийняті теоретичні уявлення та гіпотези виразити у вигляді математичних рівнянь, тобто зробити вибір раціонального типу економетричної модем.

4. Формування масиву вхідної інформації згідно з метою та завданням дослідження.

5. Оцінка параметрів моделі методом найменших квадратів та аналіз залишків (відхилень) з метою виявлення відповідності специфікацій моделей вимогам класичної лінійної моделі.

6. Якщо деякі вимоги не виконуються, то для продовження аналізу треба замінити специфікацію або застосувати інші методи оцінювання параметрів.

7. Верифікація моделі. Проведення аналізу достовірності моделі та прогнозу за побудованою моделлю.

55. Параметри моделі парної лінійної регресії, їх сутність та оцінювання.

Моделі лінійної регресії здобули найширше використання в економічних дослідженнях. В загальному вигляді теоретична модель парної регресії записується так:

де -параметри (коефіцієнти) регресії.Для визначення цих коефіцієнтів необхідно використати всі значення змінних У та Х генеральної сукупності, що практично здійснити неможливо. Отже завдання ланайного регресійного аналізу полягає в тому, щоб за наявності статистичних даних визначити найкращі статистичні оцінки для невідомих теоретичних параметрів (коефіцієнтів) .

Таким чином нам необхідно побудувати так зване емпіричне рівняння на базі інформації, одержаної із вибірки. Емпірична лінійна модель парної регресії має вигляд:

де -емпіричні коефіцієнти регресії.Їх статистичні оцінки можна визначити шляхом мінімізації суми квадратів відхилень, тобто виразу

де у_і –значення ознаки У, яку одержано зі статистичного розподілу; у_і *-значення ознаки У, яке може бути обчислено за виразом за умови визначення емпіричних коефіцієнтів .Здійснення розрахунку цих коефіцієнтів за критерієм мінімізації суми має назву методу найменших квадратів (МНК). Цей метод найбільш простий, розраховані за ним статистичні оцінки мають ряд оптимальних властивостей за дотримання певних умов.

56.Закони розподілу ймовірностей емпіричних параметрів , їх числові характерстики та статистичні властивості.

Закони розподілу.На основі центральної граничної теореми теорії ймовірностей можемо стверджувати, що випадкові величини β₀ β₁ й емпірична функція β_{0 +} β₁х_і матимуть нормальний закон розподілу ймовірностей. Тоді, здійснюючи нормування цих величин, отримаємо:

Оскільки е = у_і (β_{0 +} β₁х_і ), тобто до складу е_і входить випадкова величина β_{0 +} β₁х_і , що має нормальний закон розподілу, то на основі теореми теорії ймовірностей про побудову законів розподілу можна стверджувати, що буде розподілена за законом Х^2.

Тоді 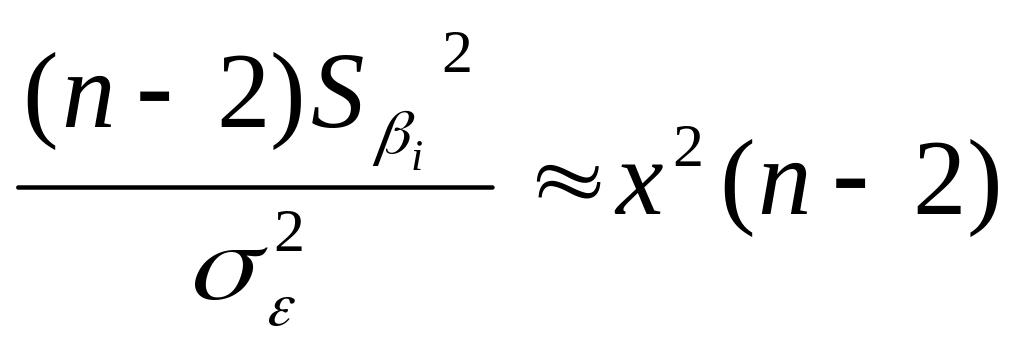(і = 0.1); , тобто мають розподіл Х² із κ = n -2 ступенем свободи. А випадкові величини тобто мають розподіл х із κ = n -2.

Числові характер.Отримане за моделлю значення залежної змінної У = у_{і =} β_{0 +} β₁х_і є випадковою величиною, бо визначається випадковими емпіричними коефіцієнтами β_0, β_1. Враховуючи це, можемо визначити для у_і основні числові характеристики, а саме:

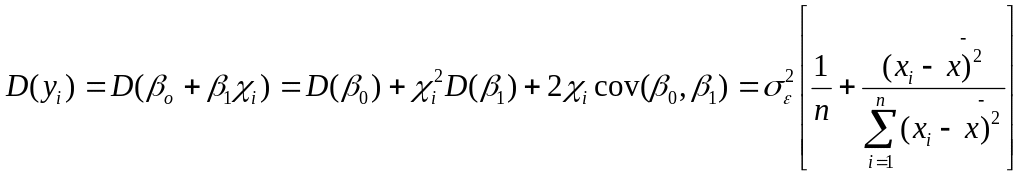
Таким чином маємо ,

,
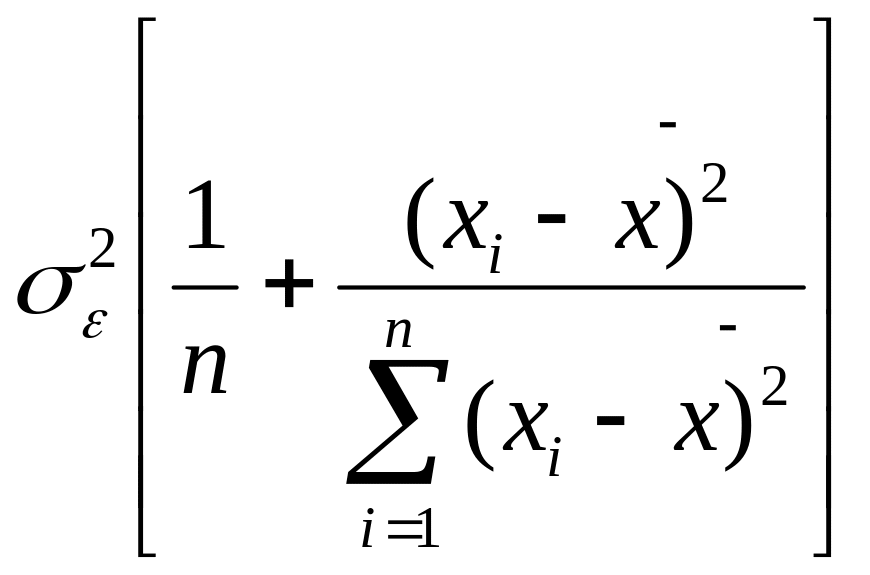