10. Ускорение Кориолиса и определение его по правилу Жуковского.

.

Ускорение называют ускорением Кориолиса. Ввиду того, что ускорение Кориолиса появляется в случае вращения подвижной системы отсчета, его называют еще поворотным ускорением.

С физической точки зрения появление поворотного ускорения точки объясняется взаимным влиянием переносного и относительного движений.

Итак, ускорение Кориолиса точки равно по модулю и направлению удвоенному векторному произведению угловой скорости переносного движения на относительную скорость точки.

Для определения направления можно также пользоваться следующим правилом Н. Е. Жу­ковского: чтобы получить направление поворот­ного ускорения , достаточно составляющую относительной скорости точки М, перпенди­кулярную к вектору , повернуть (в плоскости, перпендикулярной к вектору ) на прямой угол вокруг точки М в направлении переносного вра­щения (рис.51).

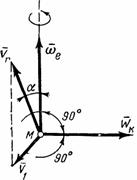
Рис.51

 

Если переносное движение подвижной систе­мы отсчета есть поступательное движение, то и поэтому поворотное ускорение точки также равно нулю. Поворотное ускорение равно, очевидно, нулю и в том случае, когда в данный момент времени обращается в нуль.

Кроме того, поворотное ускорение точки может, очевидно, обращать­ся в нуль, если:

а) вектор относительной скорости точки параллелен вектору уг­ловой скорости переносного вращения, т.е. относительное движение точки происходит по направлению, параллельному оси переносного вращения;

б) точка не имеет движения относительно подвижной системы от­счета или относительная скорость точки в данный момент времени равна нулю ( ).

12. Сложение вращений твердого тела вокруг параллельных осей.

На рис. 54 изображено тело, которое со­вершает сложное движение – вращение вокруг оси, которая сама вращается вокруг другой, не­подвижной оси. Естественно, первое вращение следует на­звать относительным движением тела, второе – переносным, а соответствующие оси обозна­чить и .

Рис.54 

Абсолютным движением будет вращение вокруг точки пересечения осей О. Угловые скорости переносного вращения и от­носительного вращения изображается векто­рами и , отложенными из неподвижной точки О, точки пересечения осей, по соответст­вующим осям.

Найдем абсолютную скорость какой-нибудь точки М тела, положение которой определяется радиусом-вектором .

Как известно, она складывается из двух скоростей, относительной и переносной: . Где , .

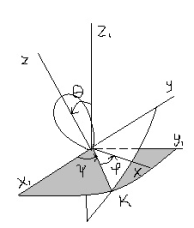А бсолютная же скорость, скорость при вращении вокруг неподвижной точки О, при сферическом движении, определяется аналогично , где - абсолютная угловая скорость, направленная по мгновенной оси вращения Р.

По формуле сложения скоростей получим: или .

Отсюда ,то есть мгновенная угловая скорость, угловая скорость абсолютного движения, есть векторная сумма угловых скоростей переносного и относительного движений. А мгновенная ось вращения P, направленная по вектору , совпадает с диагональю параллелограмма, построенного на векторах и (рис.54).

Частные случаи:

1. Оси вращения и параллельны, на­правления вращений одинаковы (рис. 55).

Рис.55 

Так как векторы и параллельны и направлены в одну сторону, то абсолютная угловая скорость по величине равна сумме их модулей и вектор ее направлен в туже сторону. Мгновенная ось вращения Р делит рас­стояние между осями на части обратно пропорциональные и :

. (Аналогично равнодействующей параллельных сил). В этом частном слу­чае тело А совершает плоскопараллельное движение. Мгновенный центр скоростей находится на оси Р.

2. Оси вращения параллельны, направления вращений противоположны (рис.56).

Рис.56 

В этом случае (при ). Мгновенная ось вращения и мгновенный центр скоростей находятся за вектором большей угловой скорости на расстояниях таких, что (опять по аналогии определения равнодействующей параллельных сил).

3. Оси вращения параллельны, направления вращений противоположны и угловые скорости равны.

Угловая скорость абсолютного движения и, следовательно, тело совершает поступательное движение. Этот случай называется парой вращений, по аналогии с парой сил.