13. Обобщенные координаты, обобщенные силы. Способы их задания и определения.

Обобщенные координаты – независимые между собой параметры любой размерности, число которых равно числу степеней свободы системы и которые однозначно определяют ее положение. q

Элементарные перемещения δq между собой также независимы. При движении системы ее обобщенные координаты будут с течением времени непрерывно изменяться qn=fn(t) –уравнения движения системы в обобщенных координатах.

Производные от обобщенных координат по времени – обобщенные скорости dq/dt.

(δrk)1=(∂rk/∂q1) δq1элементарное приращение Сумма элементарных работ :δA1=Fn(δrn)1= Fn(∂rk/∂q1) δq1 =Q1δq1Q1- обобщенная сила.

∑δAk=Qkδqk– полная элементарная работа всех действующих сил на систему в обобщенных координатах. Из равенства видно, что обобщенные силы – это величины, равные коэффициентам, при приращениях обобщенных координат в выражении полной элементарной работы действующих на систему сил. Размерность обобщенной силы равна размерности элементарной работы, деленной на размерность соответствующей обобщенной координаты.

Вычисление обобщенных сил:

Устанавливаем кол-во степеней свободы системы

Выбираем обобщенные координаты

Изображаем на чертеже приложенные к системе активные силы и силы трения.

Для определения Q1 сообщаем системе такое возможное перемещение, при котором изменяется только координата q1, получая положительное приращение δq1

Вычисляем сумму всех элементарных работ

Представляем сумму в виде δA1=Q1δq1

Вычисляем Q1из данного равенства.

Случай потенциальных сил. Если все действующие на систему силы являются потенциальными, то для системы существует такая силовая функция U, что сумма элементарных работ равна полному дифференциалу этой функции.∑δAk=δUQn=∂U/∂qnт.к. потенциальная энергия П=-U, то Qn=-∂П/∂qn - Если все действующие силы потенциальны, то обобщенные силы равны частным производным от потенциальной энергии, взятым со знаком минус, по соответствующим обобщенным координатам.

14. Уравнения равновесия в обобщенных координатах.

По определению обобщенные силы:

k = 1,2,3,…, s, где s – число степеней свободы.

Если система находится в равновесии, то по принципу возможных перемещений . Здесь – перемещения, допускаемые связями, возможные перемещения. Поэтому при равновесии материальной системы все ее обобщенные силы равны нулю:

Qk = 0, (k=1,2,3,…, s).

Эти уравнения, уравнения равновесия в обобщенных координатах или уравнения равновесия Лагранжа, позволяют решать задачи статики еще одним методом.

Если система консервативная, то Значит, в положении равновесия . То есть в положении равновесия такой материальной системы ее потенциальная энергия либо максимальна, либо минимальна, т.е. функция имеет экстремум.

Это очевидно из анализа простейшего примера (рис.73). Потенциальная энергия шарика в положении М1 имеет минимум, в положении М2 – максимум. Можно заметить, что в положении М1 равновесие будет устойчивым; в положении М2 – неустойчивым.

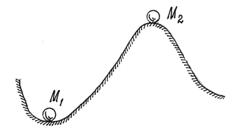
Рис.73

Равновесие считается устойчивым, если телу в этом положении сообщить малую скорость или сместить на малое расстояние и эти отклонения в дальнейшем не увеличатся.

Можно доказать (теорема Лагранжа-Дирихле), что если в положении равновесия консервативной системы ее потенциальная энергия имеет минимум, то это положение равновесия устойчиво.

Для консервативной системы с одной степенью свободы условие минимума потенциальной энергии, а значит и устойчивости положения равновесия, определяется, второй производной, ее значением в положении равновесия, .