1.Элементы комбинаторики. Сочетания. Размещение. Перестановки.

Комбинаторика - это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Основы комбинаторики очень важны для оценки вероятностей случайных событий, т.к. именно они позволяют подсчитать принципиальновозможное количество различных вариантов развития событий.

Основная формула комбинаторики

Пусть имеется k групп элементов, причем i-я группа состоит из n_i элементов. Выберем по одному элементу из каждой группы. Тогда общее число N способов, которыми можно произвести такой выбор, определяется соотношением N=n₁*n₂*n₃*...*n_k. Пример 2. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться? Решение: n₁=6 (т.к. в качестве первой цифры можно взять любую цифру из 1, 2, 3, 4, 5, 6), n₂=7 (т.к. в качестве второй цифры можно взять любую цифру из 0, 1, 2, 3, 4, 5, 6), n3=4 (т.к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4, 6). Итак, N=n₁*n₂*n₃=6*7*4=168.

В том случае, когда все группы состоят из одинакового числа элементов, т.е. n₁=n₂=...n_k=n можно считать, что каждый выбор производится из одной и той же группы, причем элемент после выбора снова возвращается в группу. Тогда число всех способов выбора равно n^k.Такой способ выбора носит название выборки с возвращением.

Пример 3. Сколько всех четырехзначных чисел можно составить из цифр 1, 5, 6, 7, 8? Решение. Для каждого разряда четырехзначного числа имеется пять возможностей, значит N=5*5*5*5=5⁴=625.

Рассмотрим множество, состоящие из n элементов. Это множество будем называть генеральной совокупностью.  Определение 1. Размещением из n элементов по m называется любой упорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.

Пример 4. Различными размещениями из трех элементов {1, 2, 3} по два будут наборы (1, 2), (2, 1), (1, 3), (3, 1), (2, 3),(3, 2). Размещения могут отличаться друг от друга как элементами, так и их порядком.

Число размещений обозначается A_n^m и вычисляется по формуле:

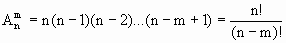
Замечание: n!=1*2*3*...*n (читается: "эн факториал"), кроме того полагают, что 0!=1.

Пример 5. Сколько существует двузначных чисел, в которых цифра десятков и цифра единиц различные и нечетные? Решение: т.к. нечетных цифр пять, а именно 1, 3, 5, 7, 9, то эта задача сводится к выбору и размещению на две разные позиции двух из пяти различных цифр, т.е. указанных чисел будет:

Определение 2. Сочетанием из n элементов по m называется любой неупорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.

Определение 3. Перестановкой из n элементов называется любой упорядоченный набор этих элементов.

Пример 7a. Всевозможными перестановками множества, состоящего из трех элементов {1, 2, 3} являются: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2).

2. горох

3. Классическое и геометрическое определение вероятностей. Классическое определение вероятности

Вероятность события численно характеризует степень возможности его появления в рассматриваемом опыте.

Пусть производится опыт с n равнозначными исходами, образующими полную группу несовместных событий. Такие исходы называются элементарными исходами (событиями), случаями, шансами. Случай, который приводит к наступлению события А, называется благоприятным (или благоприятствующим) ему.

Вероятностью события А называется отношение числа m случаев, благоприятствующих этому событию, к общему числу n случаев.

p(A)=m/n

Такое определение вероятности называется классическим определение вероятности.

Из классического определения следуют свойства вероятности:

• 0≤p(A)≤1

• p(Ø)=0,

•  p(Ω)=1,

• p(Ā)=1-p(A)

• p(A+B)= p(A)+ p(B), если AB=Ø

Геометрическое определение вероятности

Обобщением понятия "классической вероятности" на случай опытов с бесконечным (вообще говоря, несчетным) числом исходов является понятие "геометрической вероятности". К этому понятию приводят задачи на подсчет вероятности попадания точки в некую область (отрезок, часть плоскости, часть тела и т.д.).

Пусть пространство элементарных событий Ω представляет собой некоторую область плоскости. Тогда в качестве событий могут рассматриваться области А, содержащиеся в Ω.

Вероятность попадания в область А точки, наудачу выбранной из области Ω, называется геометрической вероятностью события А и находится по формуле:

p(A)=S(Ω)/S(Ω),

где S(A) и S(Ω) площади областей А и Ω соответственно.

Случай, когда Ω представляет собой отрезок или трехмерную область, рассматривается аналогично.

4. Действия над событиями. Алгебра Буля.

Действия над случайными событиями и отношения между ними определяются по аналогии с действиями и отношениями в теории множеств.

Обозначаем А, если — элементарный исход события А; А В, если событие А влечет за собой В; А, В

Равенство (эквивалентность) событий: А = В, если А В и В А.

О: Суммой событий A и В называется их теоретико-множественное объединение, т.е. событие, состоящее из элементарных событий или В.              

Произведением АВ (А В) событий А и В называется их теоретико-множественное пересечение, т.е. событие, состоящее из элементарных событий: А и В. Разностью событий Аи В называется их теоретико-множественная разность, т.е. событие, состоящее из элементарных событий но В. Противоположным событием для события A называется теоретико-множественное дополнение А до т.е.   происходит тогда, когда А не происходит.

Примеры:

1. А— выигрыш по займу 1; В — выигрыш по займу 2. Тогда А В — выигрыш хотя бы по одному из займов (в частности, сразу по двум).

2.  А — прохождение I тура на конкурсе, В — прохождение II тура. Тогда АВ — успешное прохождение I и II туров.

3.  Бросают монету. А — выпадение герба, — выпадение решки.

Множество случайных событий А и образуют булеву алгебру — алгебру событий, связанных с заданным экспериментом.

О: События А и В называются несовместными, если наступление А исключает наступление В, т.е. АВ= В этом случае используют А В = А+ В.

Таким образом А, — несовместные события.

О: Множество (система) событий

называется полной группой событий S, если

5. Теорема для сложения вероятностей для совместных событий. Теорема для сложения вероятностей не совместных событий.

Теорема. Вероятность суммы 2-х совместных событий равна сумме вероятностей этих событий без учета их совместного появления. p(A+B)=p(A)+p(B)−p(AB) 

Доказательство:

A+B=AB+AB+AB (сумма несовместных пар)

Тогда p(A+B)=p(AB)+p(AB)+p(AB)

Событие A=AB+AB,

Событие B=AB+AB

p(A+B)=p(A)−p(AB)+p(B)−p(AB)+p(AB)=p(A)+p(B)−p(AB) 

Теорема. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Р (А + В) = Р (А) + Р (В).

Введем обозначения: n — общее число возможных элементарных исходов испытания; m₁ — число исходов, благоприятствующих событию A; m₂— число исходов, благоприятствующих событию В.

Число элементарных исходов, благоприятствующих наступлению либо события А, либо события В, равно m₁ + m₂. Следовательно,

Р (A + В) = (m₁ + m₂) / n = m₁ / n + m₂ / n.

Приняв во внимание, что m₁ / n = Р (А) и m₂ / n = Р (В), окончательно получим

Р (А + В) = Р (А) + Р (В).

6. Условная вероятность. Пример. Теорема умножения вероятностей для зависимых событий. Независимые события. Теорема умножения для независимых величин.

Условная вероятность

Пример Игральная кость подбрасывается один раз. Известно, что выпало более трёх очков. Какова вероятность того, что выпало чётное число очков?

Зная, что выпало более трёх очков, мы можем сузить множество всех возможных элементарных исходов до трёх одинаково вероятных исходов:  , из которых событию  благоприятствуют ровно два:  . Поэтому  .

Посмотрим на вопрос с точки зрения первоначального эксперимента. Пространство элементарных исходов при одном подбрасывании кубика состоит из шести точек:  . Слова «известно, что выпало более трёх очков» означают, что в эксперименте произошло событие  . Слова «какова при этом вероятность того, что выпало чётное число очков?» означают, что нас интересует, в какой доле случаев при осуществлении   происходит и  . Вероятность события  , вычисленную в предположении, что о результате эксперимента уже что-то известно (событие   произошло), мы будем обозначать через  .

Мы хотим найти, какую часть составляют исходы, благоприятствующие   внутри   (т.е. одновременно   и  ), среди исходов, благоприятствующих  .

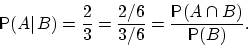
Мы пришли к выражению, которое можно считать определением условной вероятности.

УМНОЖЕНИЕ ВЕРОЯТНОСТЕЙ ЗАВИСИМЫХ СОБЫТИЙ 

     Теорема. Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них наусловную вероятность другого, вычисленную в предположении, что первое событие уже наступило:  P(AB)=P(A)P(A|B). Вероятность совместного появления трех зависимых событий:  P(ABC)=P(A)P(A|B)P(AB|C). 

Теорема об умножении вероятностей. Вероятность произведения независимых событийА и В вычисляется по формуле:

.Пример. Вероятность попадания в цель у первого стрелка 0,8, у второго – 0,9. Стрелки делают по выстрелу. Найти вероятность: а) двойного попадания; б) хотя бы одного попадания; г) одного попадания.

Решение.

Пусть А – попадание первого стрелка,  ;

В – попадание второго стрелка,  .

Тогда   - промах первого,  ;

 - промах второго,  .

Найдем нужные вероятности.

а) АВ – двойное попадание, 

б)   – двойной промах,  .

в) А+В – хотя бы одно попадание,

.

г)   – одно попадание,

7. Формула полной вероятности.

Пусть событие А может произойти только совместно с одним из событий Н1, Н2,…, Нп, образующих полную группу несовместных событий. Тогда события Н1, Н2,…, Нп называются гипотезами.

Теорема. Вероятность события А, наступающего совместно с гипотезами Н1, Н2,…, Нп, равна: 

где P(Hi) – вероятность i той гипотезы, а P(A/Hi) – вероятность события А при условии реализации этой гипотезы. Формула носит название формулы полной вероятности.

Доказательство.

Можно считать событие А суммой попарно несовместных событий АН1, АН2,…, АНп. Тогда из теорем сложения и умножения следует, что

что и требовалось доказать.

8. Формула Байеса.

 Пусть   — полная группа событий, и   — некоторое событие, вероятность которого положительна. Тогда условная вероятность того, что имело место событие  , если в результате эксперимента наблюдалось событие  , может быть вычислена по формуле:

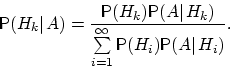
Доказательство. По определению условной вероятности,

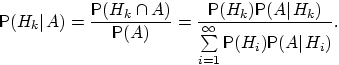
9. Сводка основных правил теории вероятности.

10. Схема с повторением независимых испытаний (схема Бернулли). Формула Бернулли.

Испытания независимы, если вероятность элементарных исходов не зависят от предыдущих испытаний.

 – число независимых испытаний  – может произойти с вероятностью  С какой вероятностью событие   произойдет   раз

, где  – вероятность успеха  – вероятность неуспеха  – число сочетаний способов

Доказательство:

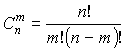
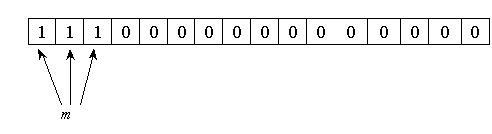
Теорема: Если Вероятность p наступления события Α в каждом испытании постоянна, то вероятность   того, что событие A наступит k раз в n независимых испытаниях, равна:  , где  .