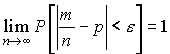Правило трех сигм

В теории вероятностей квадратичное отклонение σ_x случайной величины x (от ее математического ожидания) определяется как квадратный корень из дисперсии D_x и называют также стандартным отклонением величины x. Для любой случайной величины x с математическим ожиданием m_x и квадратичным отклонением σ_x вероятность отклонения x от m_x, больших по абсолютной величине k·σ_x, k > 0, не превосходит 1/k² (неравенство Чебышева). В случае нормального распределения указанная вероятность при k = 3 равна 0.0027. В практических задачах, приводящих к нормальному распределению, чаще всего пренебрегают возможностью отклонения от среднего, большего 3·σ_x.

18. Закон распределения Пуассона. Функция надежности. Интенсивность отказов. Показательный закон.

Распределение Пуассона — это частный случай биномиального распределения (при n >> 0 и приp –> 0 (редкие события)).

Из математики известна формула, позволяющая примерно подсчитать значение любого члена биномиального распределения:

где a = n · p — параметр Пуассона (математическое ожидание), а дисперсия равна математическому ожиданию.

Пусть элемент (то есть некоторое устройство) начинает работать в момент времени t₀ = 0 и должен проработать в течение периода времени t. Обозначим за Т непрерывную случайную величину — время безотказной работы элемента, тогда функция F(t) = p(T > t) определяет вероятность отказа за время t. Следовательно, вероятность безотказной работы за это же время равна

R(t) = p(T > t) = 1 — F(t).

Эта функция называется функцией надежности.

19. Центральная предельная теорема.

Центральная Предельная Теорема 1   Пусть   -- последовательность независимых одинаково распределенных с.в. с конечной дисперсией. Обозначим  и  . Тогда 

где   -- функция распределения стандартного нормального закона.

20. Закон Больших чисел.

 Закон больших чисел Чебышева.     Имеет место следующее утверждение. Пусть  - последовательность попарно независимых случайных величин, имеющих ограниченные в совокупности дисперсии, т. е.  для любого i. Тогда, каково бы нибыло  , справедливо соотношение

 Закон больших чисел Бернулли.     Пусть производится последовательность независимых испытаний, в результате каждого из которых может наступить или не наступить событие А, причем вероятность наступления этого события одна и та же при каждом испытании и равна р. Если событие А фактически произошло m раз в n испытаниях, то отношение m/n называют, как мы знаем, частотой появления события А. Частота есть случайная величина, причем вероятность того, что частота принимает значение m/n, выражается по формуле Бернулли (13):   

   Закон больших чисел в форме Бернулли состоит в следующем: с вероятностью, сколь угодно близкой к единице, можно утверждать, что при достаточно большом числе опытов частота появления события А как угодно мало отличается от его вероятности, т. е.

21. Неравенство Чебышева.

  неравенство Чебышева. Пусть Х – неотрицательная случайная величина (т.е.   для любого  ). Тогда для любого положительного числа а справедливо неравенство

Доказательство. Все слагаемые в правой части формулы определяющей математическое ожидание, в рассматриваемом случае неотрицательны. Поэтому при отбрасывании некоторых слагаемых сумма не увеличивается. Оставим в сумме только те члены, для которых  . Получим, что

.   (9)

Для всех слагаемых в правой части (9)  , поэтому

.   (10)

Из (9) и (10) следует требуемое.

22. Теорема Чебышева.