1. Сферическое движение АТТ. Определение. Число степеней свободы.

Сферическим движением (движением тела с одной закрепленной точкой) называется такое движение тела, при котором одна его точка О остается неподвижной во все время движения. Все остальные точки тела движутся при этом по траекториям, расположенным на поверхности сфер с центром в неподвижной точке О.

3 Степени свободы.

Углый эйлера: угол прецессии ψ, угол нутации θ, угол собственного вращения φ.

2. Теорема Эйлера.

Твердое тело с одной неподвижной точкой можно из исходного положения переместить в любое конечное положение тремя последовательными поворотами вокруг трех непараллельных осей, проходящих через неподвижную точку.

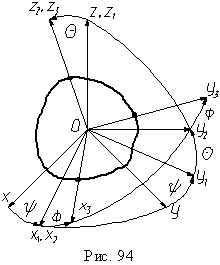
Эйлер предложил следующую последовательность поворотов. В исходном положении связанный с телом трехгранник (связанная с телом прямоугольная система координат) совпадает с неподвижной системой координат Oxyz (рис. 94). Первый поворот трехгранника производится против часовой стрелки вокруг оси Oz на угол прецессии ψ. После поворота трехгранник переходит в промежуточное положение Ox₁y₁z₁. Второй поворот производится вокруг оси Ox₁ на угол нутации θ , и трехгранник переходит в положение Ox₂y₂z₂. Третий поворот происходит вокруг оси Oz₂ на угол собственного вращения φ, а связанный с телом трехгранник займет конечное положение Ox₃y₃z₃ (рис. 94).

Так, тремя углами Эйлера определяется положение или ориентация тела в неподвижной системе отсчета, что позволяет описать сферическое движение тремя кинематическими уравнениями в углах Эйлера:

ψ = ψ(t); θ = θ(t); φ = φ(t)

Д-во: Пусть в начальный момент времени собственная система координат совпадает с осями не подвижной системы координат.

1. Повернем собственную систему на угол ψ, в положительном направлении вокруг одной из осей.

Тогда матрица преобразования:μ₁=

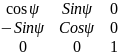
2. Теперь повернем вокруг другой из осей на угол θ.

Тогда матрица этого преобразования μ₂=

3. Повернем вокруг третьей оси на угол φ тогда μ₃=

μ= μ₃ μ₂ μ₁

3. Следствие из теоремы Эйлера.

Тк. Любое конечное движение тела я вляется вращательным то и мгновенное движение тела является вращательным вокруг некоторой оси проходящей через неподвижную точку А. А Э та ось называется мгновенной осью вращения.

Мгновенная ось вращения меняет свое положение в пространстве с течением времени.

тк. движение тела является мгновенно вращательным то скорость точки можно найти по формулам эйлера. V_m=ωXr_m

4. Кинематические уравнения Эйлера.

5. Скорость и ускорение произвольной точки АТТ в случае сферического движения.

---------------------------------------------------------------------------------------------------------------------

6. Движение свободного АТТ. Обобщенные координаты. Уравнение движения. Кинематические характеристики.

Движение свободного тела – движение без ограничений. 6 степеней свободы.

X_A=X_A(t)

Y_A=Y_A(t)

Z_A=Z_A(t) V_M=V_A+V_MA V_MA=ωXAM a_M=a_A+a_MA

ψ=ψ(t)

θ=θ(t)

φ=φ(t)

7. Скорость и ускорение точки свободного АТТ.

V_M=V_A+V_MA V_MA=ωXAM a_M=a_A+a_MA

8. Классификация мгновенных движений свободного АТТ.

______________________________________________________________________

9. Сложение движений точки. Постановка задачи. Понятие переносной угловой скорости.

Если движение точки рассматривается в двух системах координат то говорят, что тело совершает сложное движение.

Переносная угловая скорость – скорость вращения подвижной системы координат относительно неподвижной.

10. Абсолютное, относительное, переносное движение точки.

Абсолютное – движение точки в неподвижной системе отсчета.

Относительное – движение точки в подвижной системе отсчета

Переносное – движение точки закрепленной в подвижной системе отсчета, относительно неподвижной системы.

11. Лемма об абсолютной производной вектора.

Здесь мы рассмотрим как вычисляется абсолютная скорость точки, участвующей в сложном движении, доказав при этом теорему об абсолютной производной вектора.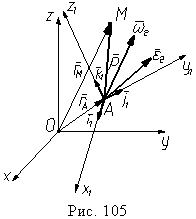

Положение точки M и начала подвижной системы координат точки A в неподвижной системе координат определим радиус-векторами r и r_A, положение точки M в подвижной системе координат определим радиус-вектором ρ, который известен в проекциях на оси подвижной системы координат, т.е. ρ = x₁i₁ + y₁j₁ + z₁k₁. На рис. 105 мы видим, что r = r_A + ρ. Аналогичное выражение было получено и для движения свободного твердого тела (п. 40). Однако в нашем случае точка M свободно перемещается в подвижной системе координат, ее радиус-вектор изменяется не только по направлению, но и по величине: ρ <> const.

Дифференцируя по времени выражение r находим абсолютную скорость точки, которая характеризует быстроту изменения положения точки в неподвижной системе координат:

(1)

где _A - абсолютная скорость начала подвижной системы координат; dρ / dt является производной вектора ρ, известного в подвижной системе координат, которую находят в неподвижной системе координат и называют абсолютной производной вектора ρ.

Найдем абсолютную производную вектора ρ:

(2)

Учитывая, что единичные векторы подвижной системы координат изменяют свое направление в пространстве, но постоянны по величине, используем формулу Эйлера для вычисления их производных, согласно которой

где ω - угловая скорость вращения подвижной системы координат в неподвижной. Поэтому сумма последних трех слагаемых в (2) равна

(3)

Первые три слагаемых в (2) характеризуют быстроту изменения вектора ρ в подвижной системе координат и их сумма называется относительной или локальной производной:

(4)

Подставляя выражения (3) и (4) в (2), получаем

(5)

Заметим, что если ρ = const, из (4) следует равенство нулю относительной производной вектора ρ, а из (5) получается формула Эйлера.

То есть мы показали справедливость формулы Эйлера и для векторов постоянных по величине, известных в произвольно двигающихся системах координат, так как здесь на движение подвижной системы координат никакие ограничения не накладывались.

Выражение (5) можно распространить и на любой другой вектор, известный в подвижной системе координат, например, b :

(6)

а затем сформулировать теорему об абсолютной производной вектора, которую иногда называют теоремой о локальной производной.

Абсолютная производная вектора равна сумме относительной (локальной) производной вектора и векторного произведения угловой скорости подвижной системы координат на сам этот вектор.

12. Теорема сложения скоростей.

Teopeмa сложения скоростей.

Пусть некоторая точка М со­вершает движение по отношению к системе отсчета Oxyz, которая са­ма движется произвольным образом по отношению к неподвижной систе­ме отсчета , (рис.49).

Конечно, абсолютное движение точки М определяется уравнениями

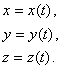Относительное движение – в движущихся осях уравнениями

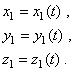
Рис. 10.3.

  Уравнений, определяющих переносное движение точки, не может быть вообще. Так как, по определению, переносное движение точки М – это движение относительно неподвижных осей той точки системы , с которой совпадает точка в данный момент. Но все точки подвижной сис­темы движутся по-разному.

Поло­жение подвижной системы отсчета может быть также определено, если задать положение точки О радиусом-вектором , проведенным из начала неподвижной системы отсчета, и направления единичных векторов подвижных осей Оx, Oy, Oz.

Рис.49

 

Произвольное переносное движение подвижной системы отсчета слагается из поступательного движения со скоростью точки О и движения вокруг мгновенной оси вращения ОР, походящей через точку О, с мгновенной угловой скоростью . Вследствие переносного движения подвижной системы отсчета радиус-вектора и направления единичных векторов изменяются. Если векторы заданы в функции времени, то переносное движение подвижной системы отсчета вполне определено.

Положение точки М по отношению к подвижной системе отсчета можно определить радиусом-вектором

,

 

где координаты x, y, z точки М изменяются с течением времени вследствие движения точки М относительно подвижной системы отсчета. Если радиус-вектор задан в функции времени, то относительное движение точки М, т.е. движение этой точки относительно подвижной системы отсчета, задано.

Положение точки М относительно неподвижной системы отсчета , может быть определено радиусом-вектором . Из рис.49 видно, что

. (1)

Если относительные координаты x,y,z точки М и векторы определены в функции времени, то слагающееся из относительного и переносного движений составное движение точки М, т.е. движение этой точки по отношению к неподвижной системе отсчета, также надо считать заданным.

Скорость составного движения точки М, или абсолютная скорость этой точки, равна, очевидно, производной от радиуса-вектора точки M по времени t

.

Поэтому, дифференцируя равенство (1) по времени t, получим

. (2)

Разобьем слагаемые в правой части этого равенства на две группы по следующему признаку. К первой группе отнесем те слагаемые, которые содержат производные только от относительных координат x,y,z, а ко второй - те слагаемые, которые содержат производные от векторов , т.е. от величин, изменяющихся только вследствие переносного движения подвижной системы отсчета

(3)

. (4)

Каждая из групп слагаемых, обозначенных через и , представляет собой, по крайней мере, по размерности некоторую скорость. Выясним физический смысл скоростей и _.

Скорость , как это следует из равенства (3), вычисляется в предположении, что изменяются только относительные координаты x,y,z точки М, но векторы остаются постоянными, т.е. подвижная система отсчета Oxyz как бы условно считается неподвижной. Итак, скорость представляет собой относительную скорость точки М.

Скорость вычисляется так, как будто бы точка М не двигалась относительно подвижной системы отсчета, так как производные x,y,z в равенство (4) не входят. Поэтому скорость представляет собой переносную скорость точки М.

Итак, . (5)

Это равенство выражает теорему сложения скоростей в случае, когда переносное движение является произвольным: абсолютная скорость точки М равна геометрической сумме переносной и относительной скоростей этой точки.