17. Д

    Рассмотрим вначале координатный способ задания движения точки. Положение в пространстве движущейся точки определяется тремя координатами в декартовой системе координат. Эти координаты задаются как функции времени:

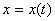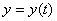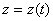    ; ; .                                            (1)

    Зависимости (1) называются уравнениями движения точки в декартовых координатах.

    Если движение точки происходит в плоскости ху, то задаются только два уравнения движения:

    ; .

    При прямолинейном движении точки достаточно задать одно уравнение движения:

    .

    Если принять, что ось х совпадает с прямой, по которой движется точка.

    Скорость точки представляет собой вектор, характеризующий быстроту и направление движения точки в данный момент времени.

    При задании движения точки уравнениями (1) проекции скорости на оси декартовых координат равны:

    ; ; .

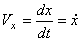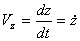    ифференциальные уравнения движения в векторной, координатной, естественной формах.

Модуль скорости

.                                           (2)

Направление скорости определяется направляющими косинусами:

Если движение точки задается в плоскости ху, то ;

;

При прямолинейном движении по оси х:

; .

Характеристикой быстроты изменения скорости является ускорение а. Ускорение точки равно производной от вектора скорости по времени:

.

При задании движения точки уравнениями (1) проекции ускорения на координатные оси равны:

; ; .

Модуль ускорения:

.                                           (3)

Направление ускорения определяется направляющими косинусами

Если движение точки задается в плоскости ху, то ; ;

;

При прямолинейном движении по оси х

; .

Далее рассмотрим естественный способ задания движения точки.

Считается, что движение точки задано естественным способом, если указаны ее траектория и закон изменения криволинейной координаты . Уравнение называется законом движения точки по траектории. При этом на траектории указывается начало отсчета, а также положительное направление отсчета координаты s в виде стрелки .

Модуль скорости точки определяется по формуле

.                                                                   (4)

Вектор скорости V направлен по касательной к траектории в сторону стрелки , если , и в противоположную сторону, если .

Ускорение точки определяется как векторная сумма касательного и нормального ускорений точки:

.

Модуль касательного ускорения определяется по формуле

.                                                     (5)

Вектор касательного ускорения направлен по касательной к траектории в сторону стрелки , если , и в противоположную, если .

Модуль нормального ускорения определяется по формуле

,                                                              (6)

где – радиус кривизны траектории в данной точке.

Вектор нормального ускорения всегда направлен по главной нормали в сторону центра кривизны траектории.

Модуль полного ускорения

.                                                            (7)

.

Модуль касательного ускорения определяется по формуле

.                                                     (5)

Вектор касательного ускорения направлен по касательной к траектории в сторону стрелки , если , и в противоположную, если .

Модуль нормального ускорения определяется по формуле

,                                                              (6)

где – радиус кривизны траектории в данной точке.

Вектор нормального ускорения всегда направлен по главной нормали в сторону центра кривизны траектории.

Модуль полного ускорения

.                                                            (7)

18. две задачи динимики точки

1) Прямая задача динамики точки

Определение равнодействующей сил, приложенных к точке по заданному закону ее движения. Пуст закон задан в декартовых координатах.

x(t)

y(t) R(t) -?

z(t)

Решение этой задачи связано с дифференцированием закона движения. Проекции и модуль равнодействующей сил находим по формулам:

Rx=mx**

Ry=my** (7)

Rz=mz**

R²= Rx²+Ry²+Rz,

Пример прямой задачи:

Найти давление автомобиля весом Р на мост радиуса R в верхней его точке, если скорость автомобиля V (Рис.3). Заметим, что давление тела на опору называется весом тела. Вес покоящегося автомобиля равен Р. Требуется найти его вес в движении. По третьему закону Ньютона этот вес будет равен нормальной реакции моста N.

Поскольку траектория движения известна, нужно воспользоваться уравнениями в естественных осях:

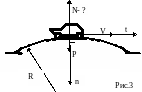
В проекции на нормаль

(P/g)(V²/R)=P-N

Значит

N=(P/g)(g-(V²/R) (8)

Чаще встречается

2. Обратная задача динамики точки,

когда по заданным функциям сил нужно найти закон движения точки.

В этом случае, уравнения в декартовых осях

mx**= Σ Fkx(x,y,z;x*,y*,z*;t)

my**= Σ Fky(x,y,z;x*,y*,z*;t) (9)

mz**= Σ Fkz(x,y,z;x*,y*,z*;t)

являются системой дифференциальных уравнениями для нахождения трех неизвестных функций времени t

x(t), y(t), z(t)

Решение этой задачи связано с интегрированием этой системы. Система имеет шестой порядок.

Значит при интегрирование возникнут шесть постоянные интегрирования и решение (второй интеграл уравнений) будет иметь вид:

x=x (t;C₁ C₂ C₃ C₄ C₅ C₆)

y=y (t;C₁ C₂ C₃ C₄ C₅ C₆) (10)

z=z (t;C₁ C₂ C₃ C₄ C₅ C₆)

Наличие постоянных интегрирования указывает на то, что у системы (9)есть множество решений, Иначе говоря силы не определяют однозначно движение точки. Одним и тем же силам могут соответствовать разные траектории движения.

Например движение камня под действием одной и той же траектории может происходить по разным траекториям в зависимости от того как его бросить (Рис.4). Произвольные постоянные интегрирования определяются из начальных условий движения.

t=0:

x=x₀ x*=x₀*

y=y₀ y*=y₀* (11)

z=z₀ z*=z₀*

Что бы определить постоянные интегрирования нужно подставить эти условия в решение (10) и его производную (первый интеграл уравнений)

x*=x* (t;C₁ C₂ C₃ C₄ C₅ C₆)

y*=y* (t;C₁ C₂ C₃ C₄ C₅ C₆) (12)

z*=z* (t;C₁ C₂ C₃ C₄ C₅ C₆)

Получим алгебраическую систему относительно постоянных C₁,...C₆ которая всегда имеет единственное решение.

Таким образом движение точки полностью определяется силами и начальными условиями.

19. Динамика относительного движения МТ. Основное уравнение динамики относительного движения МТ. Принцип относительности Галилея. Уравнение Равновесия МТ в ПСК.

Дифференциальные уравнения относительного движения

До сих пор движение материальной точки рассматривалось по отношению к инерциальной (абсолютной) системе отсчета. Именно в этой системе отсчета справедлив основной закон динамики и являющиеся следствием этого закона дифференциальные уравнения движения точки (3.2) и (3.3). Рассмотрим теперь движение точки в подвижной (неинерциальной) системе отсчета, движущейся определенным образом относительно неподвижного пространства. Как известно, для абсолютного движения основной закон динамики (3.1) имеет вид

   

Заменим входящее в данное уравнение абсолютное ускорение точки согласно формуле сложения ускорений (2.53):

 

в правой части которой стоит геометрическая сумма относительного, переносного и кориолисова ускорений.

 

или   где

величины  имеют размерность силы и называются переносной и кориолисовой силами инерции. Таким образом основной закон динамики относительного движения имеет следующий вид:

 

Сравнивая основные законы динамики абсолютного и относительного движения, приходим к следующему выводу:

 Уравнения относительного движения составляются так же, как уравнения абсолютного движения, если при этом к действующим на точку силам добавить переносную и кориолисову силы инерции.

 Добавление сил   учитывает влияние на относительное движение точки перемещение подвижной системы координат.

 Рассмотрим некоторые частные случаи относительного движения:

а) Подвижная система координат движется поступательно. В этом случае кориолисова сила инерции равна нулю так как .

б) Если подвижная система отсчета движется поступательно, равномерно и прямолинейно, то  и уравнение относительного движения не будет отличаться от уравнения абсолютного движения. Это означает, что все системы отсчета, совершающие такое движение, являются инерциальными. Кроме этого данный факт подтверждает открытый Галилеем принцип относительности классической механики:

 Никаким механическим экспериментом невозможно обнаружить, находится ли данная система отсчета в покое или совершает поступательное, равномерное и прямолинейное движение.

в) Если материальная точка находится в покое по отношению к подвижным осям, то ее относительное ускорение, относительная скорость, а следовательно и кориолисова сила инерции будут равны нулю. Уравнение относительного движение при этом превращается в уравнение относительного равновесия:

 

Из данного уравнения следует, что уравнения относительного равновесия составляются так же, как и уравнения равновесия в неподвижных осях, если при этом к действующим на точку силам взаимодействия с другими телами добавить переносную силу инерции.

г) При составлении уравнений относительного движения в случаях, когда кориолисова сила инерции не равна нулю следует учитывать, что данная сила согласно (2.54) всегда перпендикулярна относительной скорости и ее проекция на касательную к относительной траектории равна нулю, т.е. первое уравнение системы (3.3) будет иметь вид:

   

При́нцип относи́тельности — фундаментальный физический принцип, согласно которому все физические процессы в инерциальных системах отсчёта протекают одинаково, независимо от того, неподвижна ли система или она находится в состоянии равномерного и прямолинейного движения.