9. Дифференциальные уравнения плоскопараллельного движения твердого тела.

Положение тела, совершающего плоскопараллельное движение, определяется в любой момент времени положением полюса и углом поворота вокруг этого полюса. Уравнение движения точки С (центр масс) найдем по

теореме о движении центра масс Mac=∑Fek, а вращательное движение(дифференциальное уравнение вращательного движения твердого тела) Mz=Jzdω/dt в результате, проектируя сие на координатные оси, получим: Macx=∑Fekx,Macy=∑Feky,Jcdω/dt=∑mc(Fek) Md2xc/dt2 =∑Fekx,Md2yc/dt2 =∑Feky,Jcd2φ/dt2=∑mc(Fek) –эти уравнения представляют собой дифференциальные уравнения плоскопараллельного движения твердого тела.

При несвободном движении, когда траектория центра масс известна, уравнения движения точки С удобнее составлять в проекциях на касательную τ и главную нормаль nк этой траектории. Получим Mdvc/dt=∑Fekτ, Mv2c/ρc=∑Fekn, ,Jcd2φ/dt2=∑mc(Fek), ρc–радиус кривизны траектории центра масс. Заметим, что если движение является несвободным, то в уравнения войдут еще и неизвестные реакции связей.

(

Положение тела, совершающего, плоскопараллельное движение, определяется в любой момент времени положением полюса и углом поворота тела вокруг полюса. Задачи динамики будут решаться проще всего, если за полюс взять центр масс С тела (рис.58) и определять положение тела координатами XC, YC и углом .

 

Рис.58

 

На рис.58 изображено сечение тела плоскостью, параллельной плоскости движения и проходящей через центр масс С. Пусть на тело действуют внешние силы , ,... , лежащие в плоскости этого сечения. Тогда уравнения движения точки С найдём по теореме о движении центра масс

,

а вращательное движение вокруг центра С будет определятся уравнением

,

т.к. теорема, из которой получено это уравнение, справедливо и для движения системы вокруг центра масс. В результате, проектируя обе части равенства на координатные оси, получим:

, , ,

, ,

Эти уравнения представляют собой дифференциальные уравнения плоскопараллельного движения твёрдого тела. С их помощью можно по заданным силам определить закон движения тела или, зная закон движения тела, найти главный вектор и главный момент действующих сил.

При несвободном движении, когда траектория центра масс известна, уравнения движения точки С удобно составлять в проекциях на касательную и главную нормаль n к этой траектории. Тогда получим:

, , ,

где - радиус кривизны траектории центра масс.

10. Кинетическая энергия, работа и мощность. Теорема об изменении кинетической энергии.

Кинетической энергией системы называется скалярная величина Т, равная арифметиче­ской сумме кинетических энергий всех точек системы

Кинетическая энергия является характеристикой и поступатель­ного и вращательного движения системы, поэтому теоремой об изме­нении кинетической энергии особенно часто пользуются при решении задач.

Если система состоит из нескольких тел, то ее кинетическая энергия равна, очевидно, сумме кинетических энергий этих тел:

Кинетическая энергия – скалярная и всегда положительная величина.

Для характеристики действия, оказываемого силой на тело при некотором его перемещении, вводится понятие о работе силы.

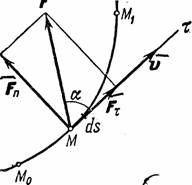
Рис.16

При этом работа характеризует то действие силы, которым определяется изменение модуля скорости движущейся точки.

Введём сначала понятие об элементарной работе силы на бесконечно малом перемещении ds. Элементарной работой силы (рис.16) называется скалярная величина:

,

где - проекция силы на касательную к траектории, направленную в сторону перемещения точки, а -бесконечно малое перемещение точки, направленное вдоль этой касательной.

Работа силы на любом конечном перемещении М0М1 вычисляется как интегральная сумма соответствующих элементарных работ и будет равна:

или .

Следовательно, работа силы на любом перемещении М0М1 равна взятому вдоль этого перемещения интегралу от элементарной работы. Пределы интеграла соответствуют значениям пере­менных интегрирования в точках М0 и М1.

Мощностью называется величина, определяющая работу, совершаемую силой в единицу времени. Если работа совершается равномерно, то мощность

,

где t - время, в течение которого произведена работа A. В общем случае

.

Следовательно, мощность равна произведению касательной состав­ляющей силы на скорость движения.

Теорема об изменении кинетической энергии точки.

Рассмотрим точку с массой т, перемещающуюся под действием при­ложенных к ней сил из положения M0 , где она имеет скорость , в положение М1 , где ее скорость равна .

Для получения искомой зависимости обратимся к уравнению выражающему основной закон динамики. Проектируя обе части этого равенства на касательную к траектории точ­ки М, направленную в сторону движения, получим:

Стоящую слева величину касательного ускорения можно пред­ставить в виде .

В результате будем иметь:

.

Умножив обе части этого равенства на ds, внесем т под знак дифференциала. Тогда, замечая, что где - эле­ментарная работа силы Fk получим выражение теоремы об изме­нении кинетической энергии в дифференциальной форме:

.

Проинтегрировав теперь обе части этого равенства в пределах, соответствующих значениям переменных в точках M0 и M1, найдем окончательно:

.

Уравнение выражает теорему об изменении кине­тической энергии точки в конечном виде: изменение кинетической энергии точки при некотором ее перемещении равно алгебраической сумме работ всех действующих на точку сил на том же перемещении.