13. Вращение тела вокруг неподвижной точки. Углы Эйлера. Кинематические уравнения Эйлера.

Положение тела и подвижной системы координат Ox1y1z1,жестко связанной с телом, определяется в неподвижной системе координат Oxyz тремя углами Эйлера (или Эйлера-Крылова). Линия ОК, вдоль которой пересекаются плоскости Ox1y1 и Oxy, называется линией узлов. Положение по отношению к осям Ox1y1z1трехгранника Oxyz, а с ним и самого тела можно определить

углами: φ=угол (KOx); ψ=(x1OK); θ=(z1Oz). Эти углы называются углами Эйлера, имеют следующие, взятые из небесной механики наименования: φ- угол собственного вращения, ψ- угол прецессии, θ – угол нутации. Уравнения движения твердого тела

вокруг неподвижной точи: :φ=f1(t); ψ=f2(t); θ=f3(t). Векторы угловых скоростей ω1 ω2ω3 – направлены соответственно по осям Oz, Oz1, OK. Движение всего тела соответственно происходит с мгновенной угловой скоростью (векторы!) ω=ω1+ ω2+ ω3. Мгновенная ось вращения – это ось, элементарным поворотом вокруг которой тело перемещается из данного положения в положение бесконечно близкое к данному. Ее направление непрерывно меняется. Мгновенное угловое ускорение – ε= dω/dt.

(

Положение тела определяется тремя углами. Используются различ­ные системы углов. Например, кора­бельные углы, самолётные углы и др. Но самыми распространёнными яв­ляются углы Эйлера: (пси), (тета), (фи).

Положение тела опре­деляется следующим образом. На­значаются две системы декартовых осей. Первая система – неподвижные оси . На­чало которых берётся в неподвижной точке тела (рис. 20). Вторая сис­тема, оси , связывается с телом. Поэтому положение тела будет опреде­ляться как положение этих осей относи­тельно неподвиж­ных.

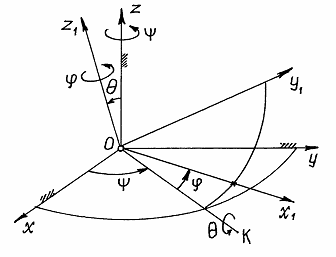
Рис.20

  Когда углы Эйлера равны нулю, под­вижные оси совпадают с непод­вижными. Чтобы опреде­лить положение тела, соот­ветст­вующее заданным углам Эйлера, производим следующие действия. Сначала подвижные оси, а значит и тело, поворачи­ваем на угол вокруг оси . При этом оси и отойдут от осей и в гори­зон­тальной плоскости и ось займёт по­ложение (рис.20). Затем тело вращаем вокруг но­вого поло­жения оси (прямой ) на угол . Ось отойдёт от оси на этот угол , а ось приподнимется над горизонтальной плоскостью. Наконец, тело (и подвижные оси) вращаем вокруг нового положения оси на угол . Ось отойдёт от положения в на­клонной плоскости, перпендикуляр­ной оси . Это положение тела и будет соответствовать углам Эйлера (на рисунке само тело не пока­зано).

Линия пересечения неподвижной плоскости и подвижной , прямая , называ­ется линией узлов. Угол называется углом прецессии, угол – углом нутации, угол – углом собственного вращения. Эти названия углов пришли из теории гироскопов.

При движении тела углы Эйлера изменя­ются по определённым законам которые называются уравнениями вра­щения.

Кинематические Э. у. дают выражения wх, wу, wz через Эйлеровы углы j, y, q и имеют вид

wx= sin q sinj + cosj,

wу= sin q cosj — sinj, (2)

wz=  + cos q.

)

ЭТО СТОИТ ЗНАТЬ!

Полукружные каналы во внутреннем ухе являются природным измерителем углового ускорения и частью вестибулярного аппарата человека. Схожесть с принципом углов Эйлера состоит в том, что три полукружных канала расположены перпендикулярно друг другу и заполнены жидкостью. Угловое ускорение по трём осям улавливается ворсинками расположенными в куполе канала, когда жидкость, желая сохранить покой, проходит черезих.

Кинематические уравнения Эйлера.

ω=ω1+ ω2+ ω3;ω1=dφ /dt, ω2=dψ/dt, ω3 =dθ/dt. Проектируем скорости на x, y, zωx=ω1x+ ω2x+ ω3x;ωy=ω1y+ ω2y+ ω3y; ωz=ω1z+ ω2z+ ω3z; ω1x= ω1y=0; ω1z= dφ /dt; ω3x= (dθ/dt)*cosφ; ω3y= - (dθ/dt)*sinφ ; ω3z=0; для определения проекции ω2 проведем через оси Oz1 и Oz плоскость, которая пересечется с плоскостью Oxyz вдоль линии OL(которая теперь перпендикулярна OK). Тогда проектируя вектор ω2 на OL, а эту проекции в свою очередь на оси Oxи Oy, получим: ω2x= (dψ/dt)*sinθ*sinφ, ω2y=(dψ/dt)*sinθ*cosφ, ω2z=(dψ/dt)*cosθ. Система следующих уравнений – система кинематических уравнений Эйлера: ωx= (dψ/dt)*sinθ*sinφ+(dθ/dt)*cosφ; ωy=(dψ/dt)*sinθ*cosφ-(dθ/dt)*sinφ;ωz= dφ /dt+(dψ/dt)*cosθ.