13. Понятие о вариационных рядах, элементы вариационного ряда, графическое изображение ряда.

Вариационным рядом называют последовательность единиц совокупности, выстроенную в порядке роста (убывания) количественного признака.

Вариационные ряды бывают дискретными и интервальными. Дискретные вариационные ряды строят обычно в том случае, если значения изучаемого признака могут отличаться друг от друга не менее чем на некоторую конечную величину. В дискретных ва­риационных рядах задаются точечные значения признака. Интервальные вариационные ряды строят обычно в том случае, если значения изучаемого признака могут отличаться друг от друга на сколь угодно малую величину. Значения признака в них за­даются в виде интервалов.

Разность между верхней и нижней границами интервала называется интервальной разностью или длиной (величиной) интервала.

В общем виде интервальную разность можно представить как: k=x_max-x_min.

Если интервал имеет обе границы, то его называют закрытым. Первый и последний интервалы могут быть от­крытыми, т. е. иметь только одну границу.

Если интервалы в "вариационном ряде имеют одинаковую длину (интервальную разность), их называют равновеликими, в противном случае — неравновеликими.

Дискретный вариационный ряд графически можно представить с помощью полигона распределения частот или частостей.

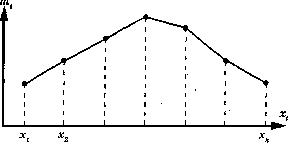Интервальные вариационные ряды графически можно представить с помощью гистограммы, т. е. столбчатой диаграммы.

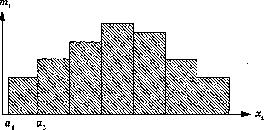При ее построении по оси абсцисс откладываются значения изучаемого признака (границы интервалов).

14. Статистические таблицы, их построение и виды.

Результат статистического наблюдения сводки и группировки обычно представляется в форме таблицы. С помощью таблицы статистический материал излагается наиболее рационально. Основанием любой таблицы является сетка, в которой вертикальные столбцы называются графами, а горизонтальные- строками. Внешне таблицы представляют собой сетку из вертикальных и горизонтальных линий, в которой записываются числовые данные. Графы (сказуемое) и строки (подлежащее) образуют макет таблицы.

В таблицах различают 2 части: 1)Подлежащие таблицы- считаю сам объект наблюдения и единицы этого объекта. 2)Сказуемое таблицы- те характеристики объекта, которые приведены в таблице.

Различают следующие виды таблиц: простые, групповые и комбинационные. Такое деление производится в зависимости от состава подлежащего. В простой таблице подлежащие не делится на группы. Простые таблицы бывают перечневые, динамические, территориальные. Так как простые таблицы дают лишь итоговую сводку и недостаточны для выявления типа изучаемого явления, его структуры и взаимосвязей, то применяются групповые и комбинационные таблицы.

Групповыми называются таблицы, в которых подлежащее разделено на группы по какому-либо одному признаку.

Комбинационными называются такие таблицы, в которых подлежащее делится на группы не по одному, а по нескольким признакам, причем каждая группа, образованная по одному признаку, делится на подгруппы по другому признаку (группировка магазина по размеру товарооборота, а затем распределение каждой группировки по площади торгового зала).