- •В.Г. Шахов основы информационных технологий
- •Введение
- •Глава 1 Теоретические основы информационных технологий
- •1.1. Теория сигналов и спектральный анализ
- •1.2. Управление колебаниями
- •1.3. Теория информации
- •1.4. Дискретизация и квантование
- •Глава 2 Сжатие информации
- •2.1. Адаптивная дискретизация, разностная и дельта-модуляция.
- •2.2. Статистическое сжатие
- •2.3 Сжатие динамического диапазона.
- •2.4. Эффективное кодирование
- •2.5. Модификации кодов Хафмана
- •2.6. Алгоритмы Лемпеля – Зива
- •2.7. Сжатие графических изображений
- •2.8. Видеостандарт mpeg
- •Глава 3 Многоканальная передача и уплотнение линий связи
- •3.1. Сравнение и анализ основных методов разделения каналов
- •3.3. Адресное разделение каналов
- •3.4. Разделение каналов на основе псевдослучайных последовательностей
- •3.5. Комбинированное разделение каналов
- •Глава 4 Случайные процессы и их приложения
- •4.1. Основы теории случайных событий и величин
- •4.2 Основы теории случайных процессов
- •Глава 5 Основы цифровой обработки сигналов
- •5.1. Дискретные экспоненциальные функции (дэф)
- •5.2. Быстрое преобразование Фурье (бпф)
- •5.3. Применение теории чисел в цифровой обработке сигналов
- •5.5. Основы цифровой фильтрации
- •Глава 6 Борьба с помехами
- •6.1. Энергетические методы
- •6.2. Методы импульсной модуляции гармонической несущей
- •6.2. Простейшие методы приема импульсных сигналов
- •6.3. Помехоустойчивый прием модулированных колебаний при импульсной огибающей
- •6.3.1 Некогерентный ам-прием
- •6.3.2 Когерентный чм-прием
- •.3.3 Когерентный фм-прием.
- •6.4.Корректирующие коды.
- •6.4.1. Основные определения корректирующих кодов.
- •6.4.2. Алгебраические коды
- •6.4.3. Матричная запись линейных корректирующих кодов
- •6.4.4. Коды Рида - Маллера I рода
- •6.4.5. Полиномиальные коды
- •6.4.6. Итеративные коды
- •6.5. Непрерывные коды
- •6.5.1. Рекуррентные коды
- •6.5.2 Сверточное кодирование
- •6.5.3. Каскадные коды
- •6.5.4. Нелинейные коды
- •6.6. Системы с обратными связями
- •6.7. Комплексные решения помехоустойчивого приема.
- •Глава 7 Пример расчета параметров информационной системы
- •7.1. Основные сведения о системах телеизмерения
- •7.2. Содержание курсовой работы и исходные данные
- •7.3. Определение полосы занимаемых частот и построение спектральной диаграммы
- •7.3.1 Определение периода опроса
- •7.3.2. Определение верхней частоты спектра импульсной последовательности
- •7.3.3. Варианты модуляции
- •7.3.4. Выбор несущих и построение спектральной диаграммы
- •7.4. Определение максимального уровня помех в канале связи
- •7.4.1. Помехоустойчивость передачи импульсно-модулированных сигналов
- •7.4.2. Помехоустойчивость передачи кодовых посылок
- •7.5. Определение количества информации одного сообщения и скорости передачи информации.
- •7.6. Вычисление эффективности передачи
- •Заключение по курсовой работе
- •Общее заключение по учебному пособию
- •Библиографический список
- •Содержание
- •Глава 7 278
Глава 2 Сжатие информации
Под
сжатием информации (или сжатием данных)
понимается устранение избыточности
сообщений. Как уже было сказано, реальные
сообщения имеют достаточно большую
избыточность. Частично избыточность
связана с повышением помехоустойчовости
(например, речь, корректирующие коды),
частично это дань способам отображения
информации (в частности, двоично-десятичный
код). Определим количественную оценку
избыточности. Если максимально допустимая
энтропия источника равна
![]() (это, например, соответствует равным
вероятностям букв русского алфавита),
а реальная
(это, например, соответствует равным
вероятностям букв русского алфавита),
а реальная
![]() ,
избыточность
,
избыточность
|
|
(2.1) |
Из
(2.1) вытекает диапазон изменения
избыточности:
![]() ,
причём, чем больше
,
причём, чем больше
![]() ,
тем меньше информационная ёмкость
сообщений. Существует несколько разных
групп методов снижения избыточности:
аппаратные, математические, лингвистические,
кодовые.
,
тем меньше информационная ёмкость
сообщений. Существует несколько разных
групп методов снижения избыточности:
аппаратные, математические, лингвистические,
кодовые.
Рассмотрим наиболее распространённые.
2.1. Адаптивная дискретизация, разностная и дельта-модуляция.
Адаптивная дискретизация осуществляется с переменным шагом, причем величина шага обратно пропорциональна производной сигнала:
|
|
(2.2) |
где
![]() – константа.
– константа.
Оценим выигрыш по эффективности, вычислив среднюю тактовую частоту. Будем считать, что выбирается по два отсчёта относительно мгновенной частоты, а она, в свою очередь, пропорциональна производной:
|
|
(2.3) |
Математическое ожидание
|
|
(2.4) |
Плотность распределения производной вычисляется для каждого распределения индивидуально по способу, изложенному, например, в [15].
Относительный проигрыш в производительности
|
|
(2.5) |
Возможны и другие способы оценивания эффективности адаптивной дискретизации [2.1], в том числе коэффициент сжатия:
|
|
(2.6) |
где
![]() – полоса частот при равномерной
дискретизации,
– полоса частот при равномерной
дискретизации,
![]() – полоса частот при адаптивной
дискретизации.
– полоса частот при адаптивной
дискретизации.
Коэффициент сжатия зависит от распределения сигнала и вида спектра; в частности, при нормальном распределении и равномерном спектре:
|
|
(2.7) |
где
![]() – максимальная амплитуда сигнала,
– максимальная амплитуда сигнала,
![]() – его с.к.о.
– его с.к.о.
Из
(2.7) видно, что чем меньше
![]() (то есть, чем уже распределение), тем
эффективнее сжатие.
(то есть, чем уже распределение), тем
эффективнее сжатие.
Структура адаптивного дискретизатора приведена на рис.2.1. Здесь УВ – устройство выборки-хранения, Д – дифференциатор. Под воздействием дифференциатора изменяется частота срабатывания УВХ. Недостатком этой схемы является наличие дифференциатора, который чувствителен к помехам, особенно импульсам и высокочастотным.
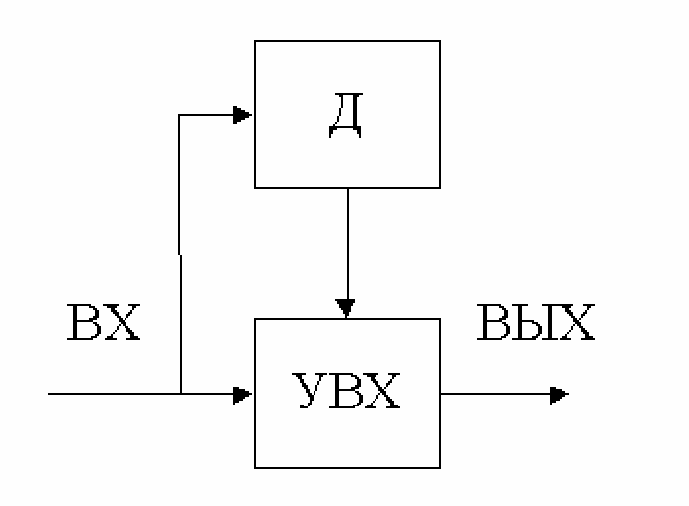
Рис. 2.1. Адаптивный дискретизатор
Лучшие характеристики имеет схема, представленная на рис. 2.2. Здесь И – интегратор.
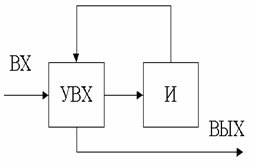
Рис. 2.2. Адаптивный дискретизатор с интегратором.
Выбор
частоты дискретизации в большой степени
зависит от способа восстановления
дискретизированного сигнала. Из раздела
1.4 следует, что восстановление по формуле
(1.118) невозможно из-за физической
нереализуемости фильтра с прямоугольной
частотной характеристикой. На практике
наиболее часто восстанавливают
непрерывное колебание с помощью полиномов
низких степеней. Выбор полиномов низкой
степени определяется снижением
эффективности аппроксимации при
дальнейшем увеличении степени. Так, при
восстановлении синусоидального колебания
полиномами первой степени вместо нулевой
с погрешностью
![]() точность возрастает в
точность возрастает в
![]() раз [7].
раз [7].
При восстановлении непрерывных колебаний возможно решение задач экстраполяции и интерполяции. В первом случае следующее значение вычисляется (восстанавливается) из предыдущего на основании знания этого значения и производной в этой точке. Метод поясняется чертежом на рис.2.3.
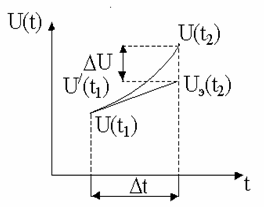
Рис. 2.3. Восстановление колебания линейной экстраполяцией
На
основании значения сигнала в точке
![]()
![]() и его производной
и его производной
![]() проводится прямая линия до момента
времени
проводится прямая линия до момента
времени
![]() .
Если за интервал времени
.
Если за интервал времени
![]() ,
производная изменится, экстраполированное
значение
,
производная изменится, экстраполированное
значение
![]() отличается от действительного
отличается от действительного
![]() на величину
на величину
![]() .
Величина
.
Величина
![]() зависит от значения второй производной
в точке
зависит от значения второй производной
в точке
![]() и минимальна при
и минимальна при
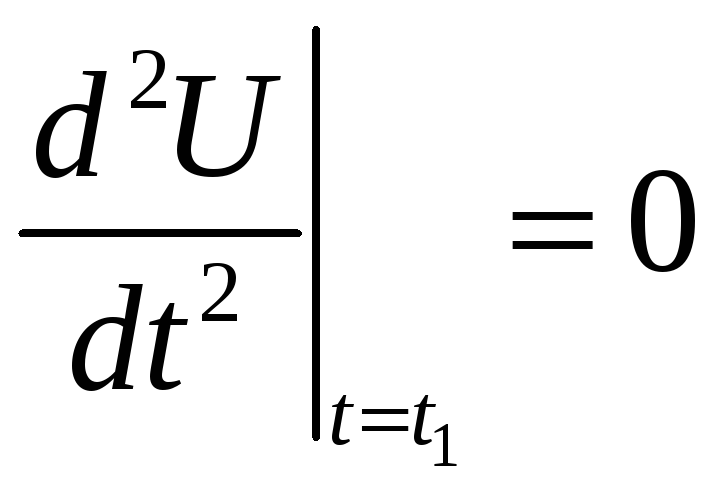 .
Если это условие не выполняется,
необходимо делать поправку с учетом
величины и знака второй производной.
.
Если это условие не выполняется,
необходимо делать поправку с учетом
величины и знака второй производной.
Интерполяция – это восстановление колебания по известным значениям. Она может выполняться по хорошо разработанным методикам, например, квадратичной аппроксимации Ньютона или с помощью полиномов Лежандра [16].
Один из широко используемых методов сжатия данных – разностная модуляция. Суть её заключается в том, что в дискретные такты передаются не абсолютные значения символов, а разности относительно предыдущих отсчётов:
|
|
(2.8) |
Оценим
эффективность этого метода, предполагая,
что сигнал
![]() непрерывный и дифференцируемый во всех
точках. На основании теоремы о конечных
приращениях выразим разность:
непрерывный и дифференцируемый во всех
точках. На основании теоремы о конечных
приращениях выразим разность:
|
|
(2.9) |
Вместо
производной можно записать частоту
![]() в предположении единичной амплитуды.
Вычислим среднее значение частоты
сигнала:
в предположении единичной амплитуды.
Вычислим среднее значение частоты
сигнала:
|
|
(2.10) |
где
![]() – спектральная плотность мощности.
– спектральная плотность мощности.
Тогда
|
|
(2.11) |
Поскольку
длина кода пропорциональна двоичному
логарифму амплитуды, сигнал предполагается
ограниченным по частоте значением
![]() ,
а по теореме Котельникова
,
а по теореме Котельникова
![]() ,
выигрыш от разностной модуляции можно
вычислить по формуле:
,
выигрыш от разностной модуляции можно
вычислить по формуле:
|
|
(2.12) |
В
наиболее неблагоприятном случае при
равномерном распределении мощности от
0 до
![]() интеграл в знаменателе равен
интеграл в знаменателе равен
![]() ,
что дает коэффициент сжатия
,
что дает коэффициент сжатия
![]() .
Наиболее часто распределение частоты
по экспоненциальному закону:
.
Наиболее часто распределение частоты
по экспоненциальному закону:
![]() .
Тогда
.
Тогда
|
|
(2.13) |
то есть, чем круче спадает характеристика, тем выше коэффициент сжатия.
Структурная схема разностного модулятора представлена на рис. 2.4. Здесь обозначено: УВХ – устройство выборки-хранения; – вычитатель аналоговых сигналов; Т – таймер (дискретизатор), К – ключ. По командам от таймера УВХ запоминает мгновенное значение сигнала с какой-то задержкой. Вначале вычитатель через ключ К заносит разность мгновенного значения входного сигнала и его предыдущего значения на АЦП, где и образуется код разности. После этого на УВХ устанавливается новое мгновенное значение сигнала.
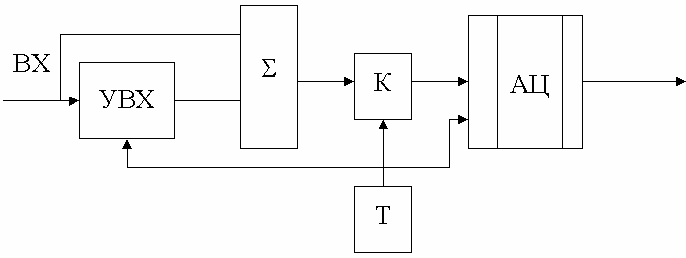
Рис. 2.4. Структура разностного модулятора
Структура демодулятора представлена на рис. 2.5. Демодулятор состоит из накапливающего сумматора и ЦАП. Поступающий на него код разности суммируется с предыдущим кодом, после чего преобразуется в аналоговую величину.
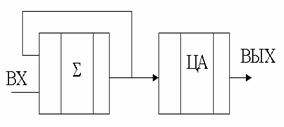
Рис. 2.5. Структура разностного демодулятора
Дельта-модуляция
– предельная ситуация разностной
модуляции [13]. Её сущность лучше
проиллюстрировать на временной диаграмме,
приведенной на рис. 2.6. Выбирается
величина шага по амплитуде
![]() ,
запоминается начальное значение сигнала
и отслеживаются изменения его амплитуды
относительно запомненного значения.
Как только текущая амплитуда изменяется
относительно этого значения на величину
,
запоминается начальное значение сигнала
и отслеживаются изменения его амплитуды
относительно запомненного значения.
Как только текущая амплитуда изменяется
относительно этого значения на величину
![]() ,
модулятор вырабатывает импульс превышения
и одновременно запоминает новое значение
сигнала. В дальнейшем процесс повторяется.
Как видно из рис.2.6, положительному
приращению сигнала соответствует
положительный импульс, отрицательному
– наоборот. Достоинством дельта-модуляции
является её очень высокая помехоустойчивость:
приёмнику достаточно отличить
положительный импульс от отрицательного.
,
модулятор вырабатывает импульс превышения
и одновременно запоминает новое значение
сигнала. В дальнейшем процесс повторяется.
Как видно из рис.2.6, положительному
приращению сигнала соответствует
положительный импульс, отрицательному
– наоборот. Достоинством дельта-модуляции
является её очень высокая помехоустойчивость:
приёмнику достаточно отличить
положительный импульс от отрицательного.
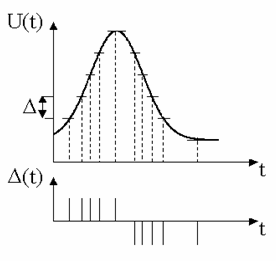
Рис. 2.6. К определению дельта-модуляции
Как
видно из рис. 2.6, частота импульсов прямо
пропорциональна производной сигнала
и обратно пропорциональна величине
приращения
![]() .
Структурная схема модулятора приведена
на рис. 2.7. Здесь обозначено: К – компаратор.
УВХ хранит предыдущее мгновенное
значение входного сигнала, компаратор
имеет характеристику идеального
трёхпозиционного реле: при положительном
приращении сигнала
.
Структурная схема модулятора приведена
на рис. 2.7. Здесь обозначено: К – компаратор.
УВХ хранит предыдущее мгновенное
значение входного сигнала, компаратор
имеет характеристику идеального
трёхпозиционного реле: при положительном
приращении сигнала
![]() он выдаёт положительный импульс, при
отрицательном – отрицательный. С каждым
импульсом компаратора УВХ запоминает
новое значение сигнала.
он выдаёт положительный импульс, при
отрицательном – отрицательный. С каждым
импульсом компаратора УВХ запоминает
новое значение сигнала.
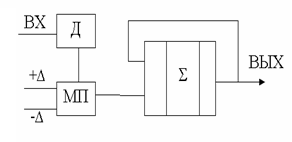
Демодулятор показан на рис. 2.8. Здесь Д – детектор полярности принимаемого импульса; МП – мультиплексор; – аналоговый сумматор. Под действием принимаемых импульсов детектор переключает мультиплексор на суммирование положительных или отрицательных приращений, а сумматор накапливает эти приращения.
|
|
|
|
Рис. 2.7. Дельта-модулятор |
Рис. 2.8. Дельта-демодулятор |
Недостатком
дельта-модуляции является специфическая
ошибка, называемая ошибкой накопления.
Сущность её заключается в том, что если
приёмник не принял один из импульсов
или принял его неверно, на выходе
появляется ошибка величины
![]() ,
которая при дальнейшей работе не
уничтожается, а накапливается. Если
канал связи симметричный, то есть
вероятности искажения положительных
и отрицательных импульсов одинаковы,
на большом интервале времени средняя
ошибка стремится к нулю, но возрастает
дисперсия ошибки. При несимметричном
канале связи дельта-модуляция вообще
неприменима, так как неизбежно приводит
к неприемлемым ошибкам.
,
которая при дальнейшей работе не
уничтожается, а накапливается. Если
канал связи симметричный, то есть
вероятности искажения положительных
и отрицательных импульсов одинаковы,
на большом интервале времени средняя
ошибка стремится к нулю, но возрастает
дисперсия ошибки. При несимметричном
канале связи дельта-модуляция вообще
неприменима, так как неизбежно приводит
к неприемлемым ошибкам.
Второй недостаток дельта-модуляции – она требует абсолютно прозрачного канала связи. Это означает, что поскольку те и другие импульсы в принципе появляются случайно во времени, канал связи между передатчиком и приёмником должен поддерживаться постоянно. Вследствие этого дельта-модуляция используется для очень низкочастотных случайных процессов. Например, это могут быть сигналы от стационарных производственных процессов (информация о частоте в энергосистеме, о давлении газа в газопроводе и т. д.).
В заключение отметим, что в некоторых случаях положительные и отрицательные импульсы заменяются кодами. Например, в системах телемеханики [41] сигналы дельта-модуляции выдаются двухразрядным двоичным кодом, в котором положительное приращение передаётся кодом 01, отрицательное – кодом 10, а отсутствие приращения – кодом 11.

 ,
,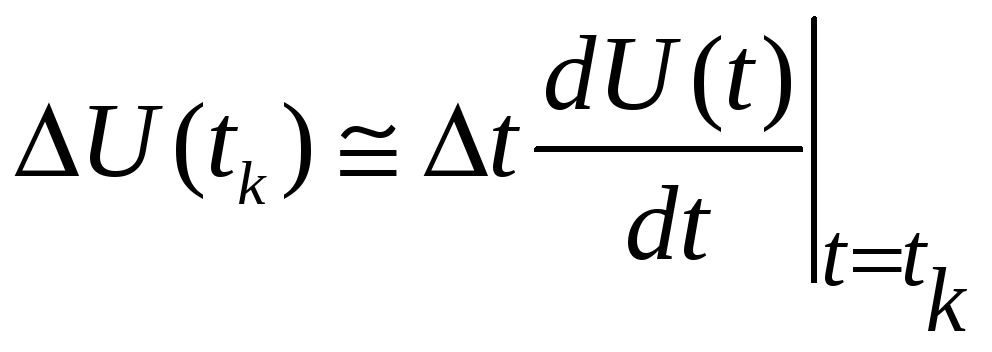 .
. .
.