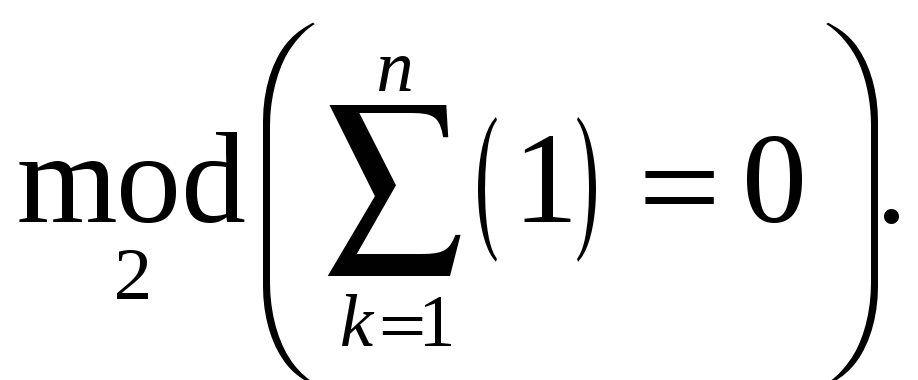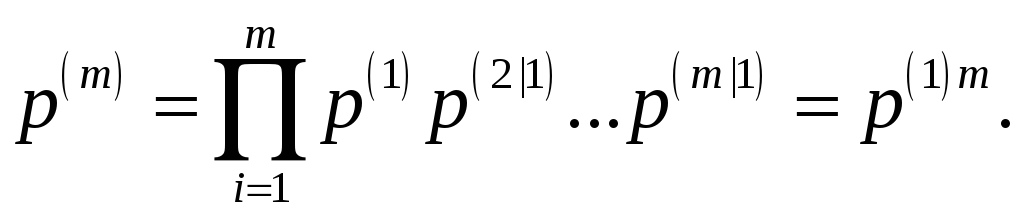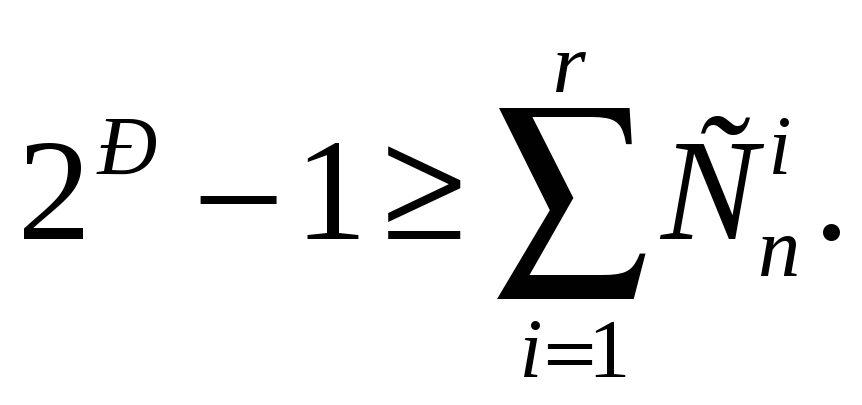6.4.Корректирующие коды.

Идея корректирующих кодов появилась в 50-е гг. прошлого века благодаря работам К. Шеннона и У. Хемминга[38,39] . Идея заключалась в том, чтобы повысить помехоустойчивость передачи введением в код дополнительных разрядов. Идея принадлежала Шеннону, а первые результаты получены Хеммингом. Суть идеи Хемминг развил в алгебраической теории помехоустойчивого кодирования, в том числе в базовых корректирующих кодах под той же фамилией.

Разобьем идею корректирующих кодов на две стадии: обеспечение помехоустойчивости на этапе зарождения и восстановление сообщения на основе существующих правил помехоустойчивого приема.

Первая стадия относится к классу алгебраических задач, с удовольствием решаемых математиками. Вторую стадию могут также решать абстрактные математики, которым нужны практические приложения. Мы с вами циники (по греческой мифологии – киники), которых больше волнуют конечный результат и практическая польза.

Вторая задача – оптимальное разрешение задачи приема корректирующего кода. Философски это достаточно разные проблемы: первая требует некоторых гарантий, вторая – механизмов оптимального восприятия. Начнем с первого уровня: гарантированного обеспечения помехоустойчивости.

6.4.1. Основные определения корректирующих кодов.

Подойдем к проблеме классическим методом. Существует некоторый объект с конечными состояниями. Необходимо обеспечить передачу этих состояний с достаточной достоверностью. На канал связи влияют помехи, и нужно обеспечить уверенное восстановление передаваемых сообщений.

Одним из гениальнейших решений поставленной задачи явилось введение дополнительных разрядов в передаваемый код. Простейший вариант – корректирующие коды, обеспечивающие помехоустойчивость.

Предположим, объект имеет N конечных состояний. Они могут описываться двоичным кодом с количеством разрядов:

(6.17)

Если при этом добавить хотя бы один разряд, можно обнаружить ошибку. Предположим, дополнительный разряд контролирует контроль на четность. В блочном коде (т. е. коде, состоящем из блоков конечной длины и разрядов) добавляется один разряд, организующий контроль. В конечном числе разрядов количество единиц кода должно быть четным:

(6.18)

Выражение (6.18) на практике реализуется достаточно просто. Принятый блочный код подается на счетный триггер (устройство, изменяющее состояние на противоположное после каждой единицы на его входе). Если количество принятых единиц четно, код пропускается на дельнейшее устройство, если нет – стирается.

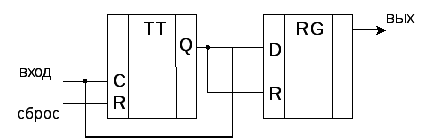
Рис. 6. 21. Контроль на четность

Передатчик работает следующим образом. Код поступает на такой же счетный триггер, предварительно установленный в 0. Если количество единиц пришедшего на триггер кода четно, на его выходе – ноль, поэтому дополнительный разряд равен 0. Приведем пример. На вход кодера (устройства, кодирующего информацию) пришли два блочных кода: 11010011 и 11010010. Используем методику контроля на четность , добавляя дополнительный разряд.

Рис. 6.22. Иллюстрация контроля на четность

В результате обе кодовые комбинации содержат четное количество единиц, что приводит к простейшему бинарному решению: если количество единиц принятого блочного кода четно, код принимается, если нет – стирается.

Такая политика называется жестким решением и может представляться в виде ориентированного графа, изображенного на рисунке 6.16. При этом требуется повторная передача того же блочного кода.

Базовые теоремы при приеме/передаче блочных кодов сводятся к двум постулатам:

1. Независимость основного сигнала и помехи. Это означает, что помеха действует независимо от кода, передаваемого по каналу.

2. Отсутствие корреляции между соседними разрядами кода (тем более между соседними кодами).

Мягкие решения – это более сложный аппарат, основывающийся на том, что на приеме вводится дополнительная зона неопределенности, в которой могут приниматься решения как бинарного типа (принять и или не принять с помощью дополнительных методик оценки) так и гладкие решения, требующие дополнительного математического аппарата. Существуют методы восстановления кодов, основанные на теории оптимизации, на дополнительных алгоритмах обработки, в том числе алгоритмах Берлекемпа-Месси, перехода в частотную область, нечетких множествах [30] .

Рис. 6.23. Граф нечетких решений

В дальнейшем сделаем упор на жесткие решения. Рассмотрим геометрическую модель корректирующих кодов. В этом случае любой двоичный код представляется в виде вершин n-мерного куба, каждая из вершин которого представляет одну из возможных кодовых комбинаций.

Корректирующие коды основаны на том, что не все возможные кодовые комбинации (КК) относятся к классу разрешенных. Это базовая идея КК. Из свойств двоичных кодов следует, что n-разрядная КК имеет количество допустимых комбинаций . Из множества разрешенных комбинаций КК выбирается .

Обозначим количество дополнительных (корректирующих) разрядов через p. Тогда очевидно, что:

(6.19)

Количество разрядов p определяет избыточность КК. В принципе, чем больше избыточность, тем больше корректирующая способность кода; фактически очень многое зависит от способа кодирования.

Введем следующие определения. Прежде всего – это кодовое расстояние. С позиции геометрической модели (n-мерный куб) рассмотрим вначале разрешенные и запрещенные КК. Последние относятся к жестким решениям и удаляются при приеме. Кодовое расстояние – это минимальная разница между двумя разрешенными КК. На геометрической модели разрешенная КК соответствует одной из вершин n-мерного куба, а кодовое расстояние – количеству ребер оптимального маршрута, проходящего между двумя разрешенными КК.

Проще интерпретируется алгебраическая модель, согласно которой две соседних разрешенных КК поразрядно суммируются по модулю 2, а количество единиц в сумме и есть кодовое расстояние d.

Приведем пример. Рассмотрим два соседних кода на рисунке 6.23 (соседними называются безызбыточные коды, отличающиеся одним разрядом). Суммируя их поразрядно по модулю 2, получим:

Рис. 6.24. Вычисление кодового расстояния.

Символ означает сложение по модулю 2, т. е. таблицу сложения вида: 00=0; 01=10=1; 11=0. Из приведенного примера получили, что кодовое расстояние d = 2. Это позволяет обнаружить одиночные ошибки (но не двойные). Допустим, в исходном корректирующем коде произошли две ошибки: при приеме код 110100111 исказился до (подчеркнуты разряды с ошибками). Контроль на четность приведет к положительному результату (т. е. к принятию решения, что КК относится к классу разрешенных), что неправильно.

Применим теперь гипотезу независимости ошибок при их повышенной кратности. Она свидетельствует о том, что ошибки повышенной кратности менее вероятны. Это вытекает из рассмотренных выше постулатов. Так как мы приняли гипотезу о независимости ошибок в соседних разрядах, то к ним применима формула Байеса:

(6.20)

Здесь обозначено: – вероятность одиночной ошибки; – вероятность двойной ошибки; – вероятность условной ошибки (при условии, что произошла ошибка в следующем разряде при наличии ее предыдущем разряде).

Поскольку все вероятности меньше 1, окончательный результат меньше вероятности одиночной ошибки. Обобщим выражение (6.20) на случай m-кратной ошибки:

(6.21)

Из выражения (6.21) следует:

(6.22)

т. е. ошибки большей кратности менее вероятны. Это лежит в основе алгоритмов жесткого декодирования.

Применим плоскую модель n-мерного куба, представив ее в виде графа с количеством исходных вершин (комбинация типа 000…00 обычно не считается) и количеством конечных вершин (с добавленными контрольными разрядами). Каждая дуга графа описывает один из возможных переходов при передаче. Они образуют три группы:

1. кодовая комбинация принята без искажений. Это соответствует сплошной дуге типа 1–1; 2–3 и т.д.

Рис. 6. 25. Графовая модель помехоустойчивого приема

2. Искажение присутствует, но оно или обнаруживается или исправляется. В данном варианте рассмотрены только обнаруживаемые ошибки типа дуги 1–2. Принятый при этом код отбрасывается. Возможно и восстановление КК путем исправления обнаруженных ошибок, что иллюстрируется рисунком 6.26. Здесь, как и раньше, дуги 1–1 и 5–5 соответствуют отсутствию ошибок; дуги 1–2 и 2–4 предполагают восстановление кода путем исправления искаженных разрядов; дуги 1–3 и 2–3 соответствуют неопределенным ситуациям и должны исключаться (т. е. коды должны стираться).

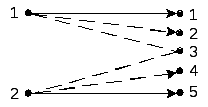
Рис. 6.26. Граф при исправлении ошибок

3. Если представить переход из вершин 1 в 4 или 5, а из 2 – в 1 или 2, попытка исправления приведет к искажению правильного разряда, что в практике называется размножением ошибок.

Эта ситуация может распространяться на более общие случаи. В частности, для графа 6.26 кодовое расстояние ; при этом возможно исправление одиночных ошибок. Если обозначить количество обнаруживаемых ошибок через s, а исправляемых через r, то справедливы следующие соотношения:

(6.23)

Очевидно, исправление ошибок требует больших ресурсов, т. е. большего кодового расстояния.

При жестком декодировании используется так называемый синдромный метод. Он заключается в том, что на передающей части по k информационным разрядам вычисляются контрольные разряды:

(6.24)

Правила вычисления дополнительных разрядов определяются типом кода.

При приеме кода вычисляются синдромные разряды по обратимой функции:

(6.25)

Здесь – разряды синдрома ошибки; – признак обратимой функции.

В теории синдромного декодирования принята гипотеза независимости ошибок по всей длине кода. Если блочный код имеет длину n разрядов, то количество одиночных ошибок – определяется как число сочетаний из n по одному:

.

(6.26)

Количество ошибок кратности 2 вычисляется как число сочетаний из n по 2:

(6.27)

Можно продолжить эти выражения. В данном случае нас интересует синдром ошибки. Существует вполне логичное выражение, которое означает, что количество различных синдромов должно быть больше количества различных ошибок. Если для -разрядного синдрома количество различных кодовых комбинаций равно , то количество различных ошибок запишется как сумма выражений (6.26) и (6.27) и им подобных. Тогда образуется фундаментальное правило синдромного декодирования:

(6.28)

Выражение (6.28) означает, что левая, синдромная, часть должна быть больше количества распознаваемых ошибок. Выражение (6.28) называется нижней границей Хемминга. Оно не связано со способом декодирования и определяет только минимальное количество дополнительных разрядов, достаточное для синдромного декодирования.

Приведем пример. Предположим, что исходный (безызбыточный) код имеет 11 разрядов. Необходимо вычислить, сколько дополнительных разрядов необходимо, чтобы код исправлял двойные ошибки. Задача решается методом итераций. Предположим, . Тогда 2⁷-1=255. Согласно нижней границе Хемминга:

Не проходит. Увеличиваем до 8:

Условие выполняется. Следовательно, для исправления двойных ошибок необходимо как минимум 8 дополнительных разрядов.

Приведенные соотношения играют роль ограничений снизу.

Примем к рассмотрению еще одно соотношение. Для этого вспомним, что ошибки друг от друга не зависят, а при их повышенной кратности используется формула Байса.

Введем обозначение обратной вероятности ошибки: q=1 - p. Эта величина приводится в теории случайных чисел для описания полной группы. Если описывать вероятность r - кратной ошибки для блочного n - разрядного кода, то окончательное выражение для r-кратной ошибки примет вид:

(6.29)

Это очень важное соотношение, которое характеризует жесткое (синдромное) декодирование.

Во второй половине ХХ века было предложено достаточно много алгоритмов кодирования/декодирования при заданной корректирующей способности кода и его длине.

Простейшая классификация корректирующих кодов приведена на рисунке 6.27. Они разделяются, во-первых, на две основных группы, блочные и непрерывные. В последнем случае код идет сплошным потоком, а помехоустойчивость обеспечивается корректирующими разрядами, встраиваемыми в поток.

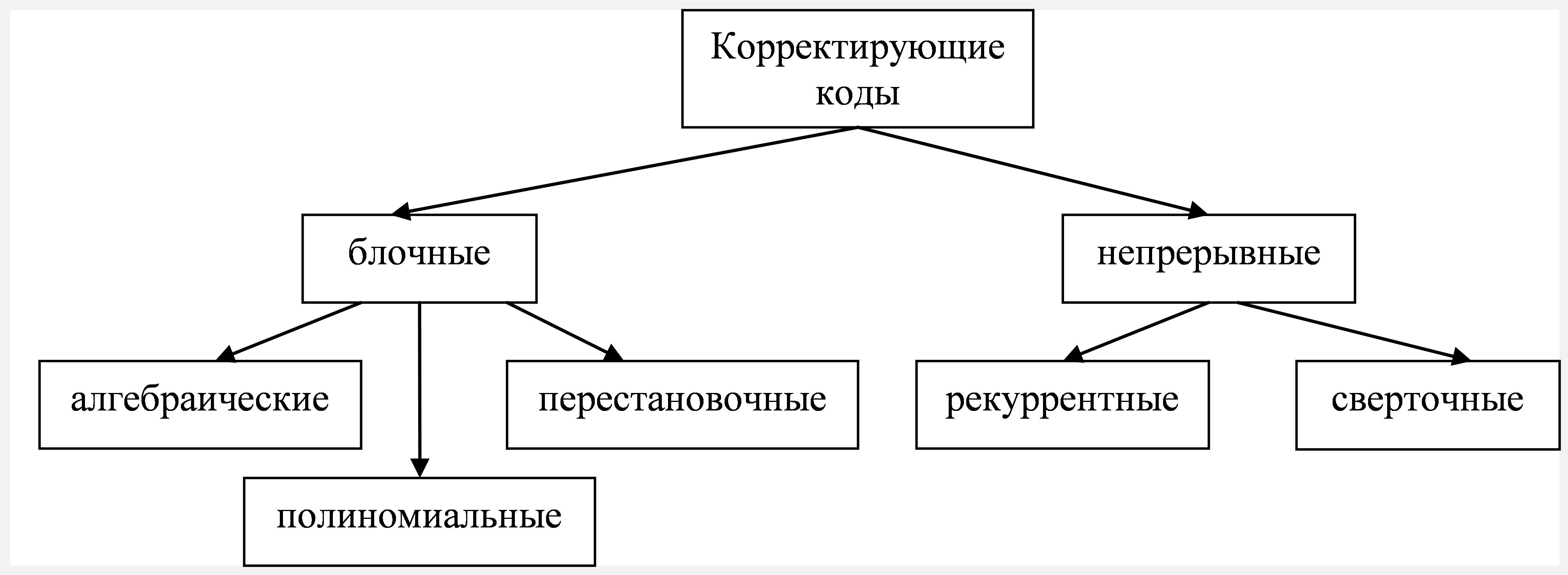
Рис. 6.27. Классификация корректирующих кодов

Остальные градации по рисунку (6.28) будем рассматривать по ходу изложения.