
- •В.Г. Шахов основы информационных технологий
- •Введение
- •Глава 1 Теоретические основы информационных технологий
- •1.1. Теория сигналов и спектральный анализ
- •1.2. Управление колебаниями
- •1.3. Теория информации
- •1.4. Дискретизация и квантование
- •Глава 2 Сжатие информации
- •2.1. Адаптивная дискретизация, разностная и дельта-модуляция.
- •2.2. Статистическое сжатие
- •2.3 Сжатие динамического диапазона.
- •2.4. Эффективное кодирование
- •2.5. Модификации кодов Хафмана
- •2.6. Алгоритмы Лемпеля – Зива
- •2.7. Сжатие графических изображений
- •2.8. Видеостандарт mpeg
- •Глава 3 Многоканальная передача и уплотнение линий связи
- •3.1. Сравнение и анализ основных методов разделения каналов
- •3.3. Адресное разделение каналов
- •3.4. Разделение каналов на основе псевдослучайных последовательностей
- •3.5. Комбинированное разделение каналов
- •Глава 4 Случайные процессы и их приложения
- •4.1. Основы теории случайных событий и величин
- •4.2 Основы теории случайных процессов
- •Глава 5 Основы цифровой обработки сигналов
- •5.1. Дискретные экспоненциальные функции (дэф)
- •5.2. Быстрое преобразование Фурье (бпф)
- •5.3. Применение теории чисел в цифровой обработке сигналов
- •5.5. Основы цифровой фильтрации
- •Глава 6 Борьба с помехами
- •6.1. Энергетические методы
- •6.2. Методы импульсной модуляции гармонической несущей
- •6.2. Простейшие методы приема импульсных сигналов
- •6.3. Помехоустойчивый прием модулированных колебаний при импульсной огибающей
- •6.3.1 Некогерентный ам-прием
- •6.3.2 Когерентный чм-прием
- •.3.3 Когерентный фм-прием.
- •6.4.Корректирующие коды.
- •6.4.1. Основные определения корректирующих кодов.
- •6.4.2. Алгебраические коды
- •6.4.3. Матричная запись линейных корректирующих кодов
- •6.4.4. Коды Рида - Маллера I рода
- •6.4.5. Полиномиальные коды
- •6.4.6. Итеративные коды
- •6.5. Непрерывные коды
- •6.5.1. Рекуррентные коды
- •6.5.2 Сверточное кодирование
- •6.5.3. Каскадные коды
- •6.5.4. Нелинейные коды
- •6.6. Системы с обратными связями
- •6.7. Комплексные решения помехоустойчивого приема.
- •Глава 7 Пример расчета параметров информационной системы
- •7.1. Основные сведения о системах телеизмерения
- •7.2. Содержание курсовой работы и исходные данные
- •7.3. Определение полосы занимаемых частот и построение спектральной диаграммы
- •7.3.1 Определение периода опроса
- •7.3.2. Определение верхней частоты спектра импульсной последовательности
- •7.3.3. Варианты модуляции
- •7.3.4. Выбор несущих и построение спектральной диаграммы
- •7.4. Определение максимального уровня помех в канале связи
- •7.4.1. Помехоустойчивость передачи импульсно-модулированных сигналов
- •7.4.2. Помехоустойчивость передачи кодовых посылок
- •7.5. Определение количества информации одного сообщения и скорости передачи информации.
- •7.6. Вычисление эффективности передачи
- •Заключение по курсовой работе
- •Общее заключение по учебному пособию
- •Библиографический список
- •Содержание
- •Глава 7 278
5.2. Быстрое преобразование Фурье (бпф)
Преобразование является базовым в множестве технических приложений. Объективным является то, что сам механизм преобразования является интегрирующим, т. е. усредняет возможные выбросы наблюдаемого случайного процесса.
В
ходе преобразования производится
переход от конечного числа
![]() точек дискретных отсчетов во времени
(согласно теореме Котельникова) к
преобразованиям в частотной области.
точек дискретных отсчетов во времени
(согласно теореме Котельникова) к
преобразованиям в частотной области.
Поиск гармонических составляющих в базисе ДЭФ и обратное преобразование имеют следующую форму:
|
|
(5.12) |
Здесь
символ
![]() означает комплексно сопряженную функцию
(в соответствии ДЭФ).
означает комплексно сопряженную функцию
(в соответствии ДЭФ).
Обратимся
к выражению (5.10). Каждое из выражений
прямого и обратного преобразований
(соответственно первая и вторая формулы)
требуют
![]() умножений комплексных чисел и столько
же сложений. Известно, что умножения
комплексных чисел удобнее выполнять в
показательной форме:
умножений комплексных чисел и столько
же сложений. Известно, что умножения
комплексных чисел удобнее выполнять в
показательной форме:
![]() ,
а сложение – в алгебраической:
,
а сложение – в алгебраической:
![]() .
В ходе преобразований для упрощения
вычислений производятся переходы из
одной формы представления в другую и
наоборот. На это тоже необходимо время.
.
В ходе преобразований для упрощения
вычислений производятся переходы из
одной формы представления в другую и
наоборот. На это тоже необходимо время.
В 1964 г. Кули и независимо от него Тьюки предложили идею сокращения количества вычислений, которые и послужили основой для первой реализации БПФ. Для конкретизации алгоритма распишем первое выражение (5.12) в показательной форме:
|
|
(5.13) |
Примем
теперь, что
![]() – четное число. Тогда сумму в (5.13) можно
представить в виде двух полусумм –
четной и нечетной:
– четное число. Тогда сумму в (5.13) можно
представить в виде двух полусумм –
четной и нечетной:
|
|
(5.14) |
После
такого разделения получается
![]() сложений и столько же умножений. Отметим,
что для любого целого
сложений и столько же умножений. Отметим,
что для любого целого
![]() справедливо неравенство:
справедливо неравенство:
|
|
(5.15) |
что означает сокращение общего количества вычислительных операций.
Применим
эту процедуру дальше: разобьем каждое
подмножество из
![]() отсчетов напополам. Эта процедура может
повторяться до тех пор, пока в подмножестве
не останется по одной точке.
отсчетов напополам. Эта процедура может
повторяться до тех пор, пока в подмножестве
не останется по одной точке.
Для дальнейшей иллюстрации метода преобразуем (5.14) к виду:
|
|
(5.16) |
Здесь
во второй сумме появляется поворачивающий
множитель
![]() ,
функция которого сводится к повороту
вектора на фазу
,
функция которого сводится к повороту
вектора на фазу
![]() .
При изменении номера гармонической
составляющей изменяются и значения
поворачивающих множителей, причем при
поэтапном преобразовании они накапливаются.
.
При изменении номера гармонической
составляющей изменяются и значения
поворачивающих множителей, причем при
поэтапном преобразовании они накапливаются.
На последнем этапе преобразования из двух исходных точек получаются две конечных комплексно сопряженных величины. Конечная операция может быть проиллюстрирована рис. 5.7.
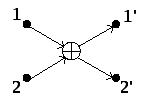
Рис. 5.7. Элементарное преобразование при БПФ
Здесь
представлен граф элементарного
преобразования, в котором участвуют
две комплексные величины (вершины 1 и
2), а в результате образуются две комплексно
сопряженных величины, обозначенных на
графе вершинами 1' и 2'. Дуга графа со
стрелкой обозначает умножение на
поворачивающий множитель
![]() ,
знак
,
знак
![]() означает сложение двух комплексных
чисел. После сложения образуются два
комплексно сопряженных числа:
означает сложение двух комплексных
чисел. После сложения образуются два
комплексно сопряженных числа:![]() и
и
![]() .
.
Полученный граф носит название «бабочка» и является базовой операцией для всех операций БПФ. В качестве примера приведем граф БПФ для восьми точек. Он показан на рисунке 5.8.
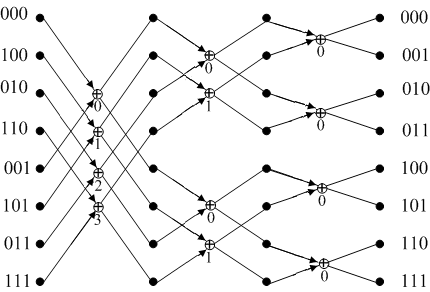
Рис.
5.8. БПФ при
![]()
Граф
содержит три сегмента по числу разбиений
по степени двойки:
![]() .
Очевидно, что для
.
Очевидно, что для
![]() будет 4 ступени преобразования. Умножающие
коэффициенты расписаны в виде фаз, где
соответствующая цифра означает поворот
фазы относительно общего базиса из
будет 4 ступени преобразования. Умножающие
коэффициенты расписаны в виде фаз, где
соответствующая цифра означает поворот
фазы относительно общего базиса из
![]() точек. Так, для
точек. Так, для
![]() цифра 3 означает поворот на
цифра 3 означает поворот на
![]() радиан.
радиан.
Обратите внимание на то, что само преобразование строго регулировано. Исходя из приведенного примера по методу индукции, легко догадаться, что граф БПФ для 16 точек включает два 8-точечных графа с дополнением четвертой ступени «сшиваются» графы с рисунка 5.8. Причем на последнем этапе происходит объединение подгрупп по принципу «две на восемь», а умножающие (поворачивающие) множители имеют значение 0,1,…7.
Обратим внимание на цифры слева и справа от графа. Это двоичные коды номеров исходных отсчетов (слева на графе код двоичный, т. е. код 101 означает в десятичной форме число 5).
Из приведенных кодов получаем, что спектральные составляющие претерпевают двоичную инверсию разрядов. Термин изобретен теми же соавторами и означает, что при инверсии разрядов код считывается в другом порядке. Так, исходный код 001 выглядит как 100.
Если посмотреть на исходные и конечные коды, то можно обнаружить, что существуют симметричные и несимметричные кодовые комбинации. Первый термин означает, что коды читаются в обе стороны одинаково. Симметричными в трехразрядном двоичном коде будут комбинации 000, 111, 010, 101; остальные – несимметричные.
Существует
второй подход к формированию БПФ. В нем
исходное множество точек просто «рубится»
на две равные части: от 0 до
![]() и от
и от
![]() до
до
![]() .
Не обращая внимания на математические
тонкости, касающиеся четных или нечетных
значений
.
Не обращая внимания на математические
тонкости, касающиеся четных или нечетных
значений
![]() (как округлять в том или другом вариантах),
отметим, что на практике значения
(как округлять в том или другом вариантах),
отметим, что на практике значения
![]() не меньше
не меньше
![]() ,
что приводит к погрешности округления
,
что приводит к погрешности округления
![]() .
Это технически оправдано, поэтому
выражения
.
Это технически оправдано, поэтому
выражения
![]() или
или
![]() могут считаться тождественными.
могут считаться тождественными.
Существует
вторая форма БПФ, когда исходную
комбинацию из
![]() точек разбивают по принципу
«располовинивания» от 0 до
точек разбивают по принципу
«располовинивания» от 0 до
![]() и от
и от
![]() до
до
![]() .
Выражение (5.13) в этом случае принимает
вид:
.
Выражение (5.13) в этом случае принимает
вид:
|
|
(5.17) |
Во
втором слагаемом сделаем замену
переменной:
![]() .
Тогда выражение (5.19) приводится к виду:
.
Тогда выражение (5.19) приводится к виду:
|
|
(5.18) |
Во
второй сумме сделаем замену переменной:
![]() .
Тогда выражение (5.18) примет вид:
.
Тогда выражение (5.18) примет вид:
|
|
(5.19) |
Оно служит основанием для другого класса преобразований, которое в интерпретации (5.19) принимает вид графа, изображенного на рис. 5.9.
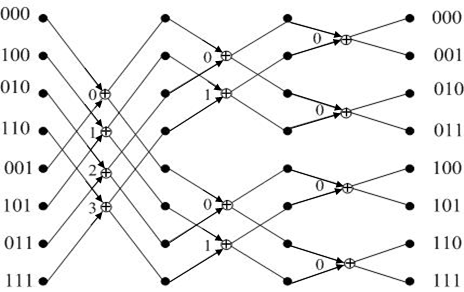
Рис. 5.9. Вторая форма БПФ
Как
видим, граф БПФ принимает форму, зеркально
симметричную относительно предыдущей
версии. Отличия заключаются в обратной
трактовке перечисления исходных данных
и их результатов. Обе формулы идентичны
и нуждаются лишь в корректировке
результатов. Последний граф легко
интерпретируется для
![]() более высоких порядков и строится по
методу итераций.
более высоких порядков и строится по
методу итераций.
В последовавшем за изобретением БПФ развитии ЦОС можно выделить два направления:
– изменения в алгоритмах обработки сигналов;
– изменения в базисе структурной обработки.
К первому направлению относится многомерная цифровую обработку. Одним из вариантов такой обработки является так называемый алгоритм Винограда.
В
основе алгоритма Винограда лежит
многомерный подход. Его суть заключается
в следующем. Исходное количество отсчетов
![]() может представляться не только как
степень двойки или любого другого целого
числа (функции Виленкина-Крестенсона,
ВКФ), но и могут раскладываться в
многомерных координатах. Если по каждой
координате произвести отдельные цифровые
преобразования, то в конечном результате
получается выигрыш по производительности.
может представляться не только как
степень двойки или любого другого целого
числа (функции Виленкина-Крестенсона,
ВКФ), но и могут раскладываться в
многомерных координатах. Если по каждой
координате произвести отдельные цифровые
преобразования, то в конечном результате
получается выигрыш по производительности.
Рассмотрим
простейший алгоритм Винограда. Имеется
исходное количество точек
![]() ,
которое можно представить в виде
произведения
,
которое можно представить в виде
произведения
![]() ,
где
,
где
![]() и
и
![]() – целые числа. Каждое из чисел можно
представить в виде одной из координат
измерения; в простейшем варианте это
простые числа. Алгоритм сводится к
следующим шагам:
– целые числа. Каждое из чисел можно
представить в виде одной из координат
измерения; в простейшем варианте это
простые числа. Алгоритм сводится к
следующим шагам:
1. после разбиения по каждой координате производится БПФ, полученные координаты образуют новый базис для системы преобразований;
2.
по выбранной новой системе координат
образуется новая совокупность данных.
Предположим, исходное количество точек
отсчета
![]() может представиться в виде двумерной
матрицы размером
может представиться в виде двумерной
матрицы размером
![]() :
:
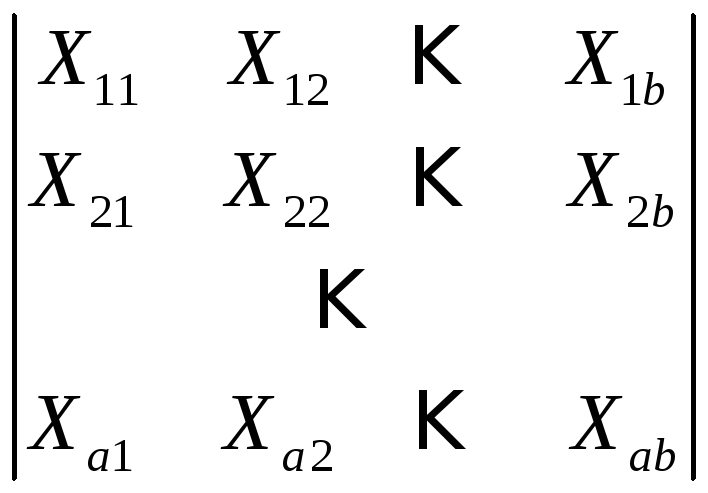
Рис. 5.10. Двумерная матрица отсчетов
Виноград предположил, что по каждому измерению может производиться независимый БПФ-анализ. Для согласования координат он ввел согласующие множители:
|
|
(5.20) |
Алгоритм
может быть продолжен на любое количество
измерений, но его эффективность снижается
пропорционально увеличению
![]() и количества координат. Если количество
координат равно
и количества координат. Если количество
координат равно
![]() ,
а количество измеренных точек по каждой
координате равно
,
а количество измеренных точек по каждой
координате равно
![]() ,
где
,
где
![]() ,
то общая эффективность алгоритма
Винограда
,
то общая эффективность алгоритма
Винограда
![]() выражается соотношением:
выражается соотношением:
|
|
(5.21) |
Алгоритм следующий:
1.
выбирается разбиение
![]() ,
при разбиении желательно, чтобы
,
при разбиении желательно, чтобы
![]() и
и
![]() были координатами, кратными степени 2;
были координатами, кратными степени 2;
2. по каждой координате возможно ДПФ. Лучше, если бы эта координата была кратна степени числа 2, тогда по этой координате проводится БПФ;
3. полученные координаты (отсчеты) умножаются на поворачивающие множители типа (5.20);
4.
результаты умножений образуют новую
матрицу. Проводится БПФ по каждому
столбцу. Результат этого преобразования
имеет размерность
![]() и в конечном счете представляет собой
результаты БПФ.
и в конечном счете представляет собой
результаты БПФ.
Приведенный
алгоритм представляет собой вариант
ускорения вычислений. Он абсолютно
сходится и имеет множество продолжений
как в количестве измерений (количестве
разбиений
![]() ),
так и в возможных вариантах разбиений.
),
так и в возможных вариантах разбиений.
Возможны многомерные варианты алгоритма Винограда, когда отсчеты формируются в трех- и более мерную матрицу. Они используются редко, так как относительная эффективность возрастает незначительно.

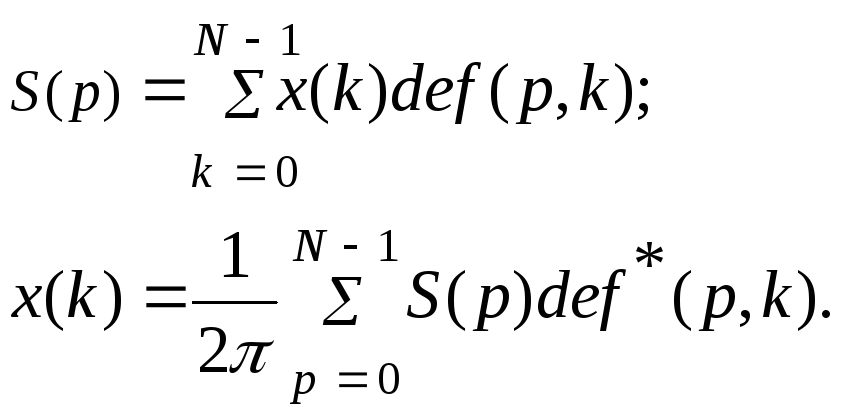
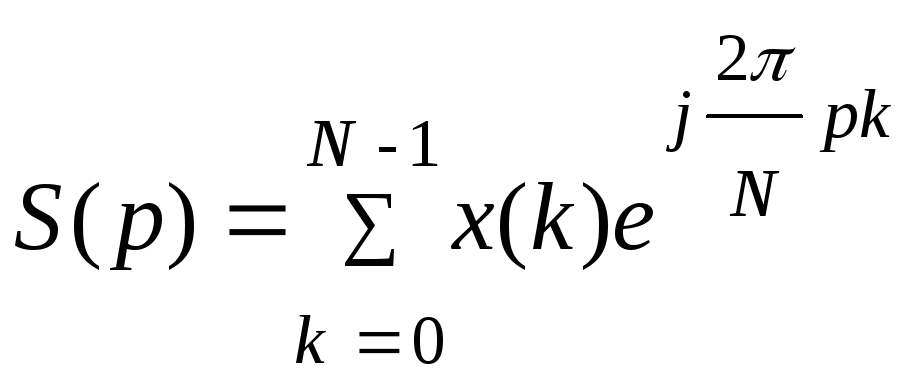 .
.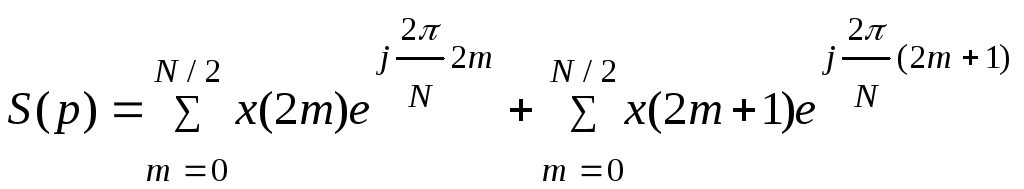 .
.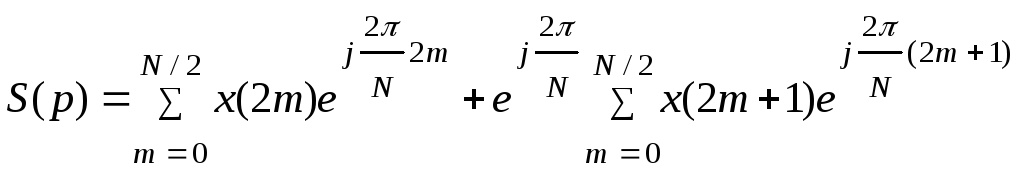 .
.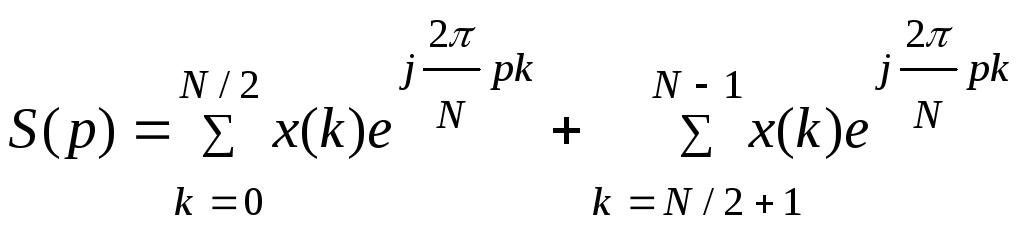 .
.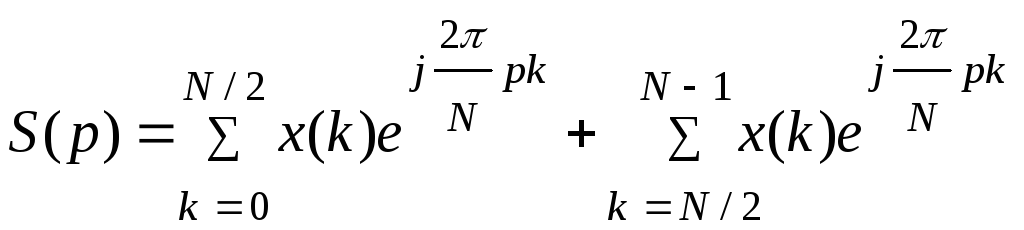 .
.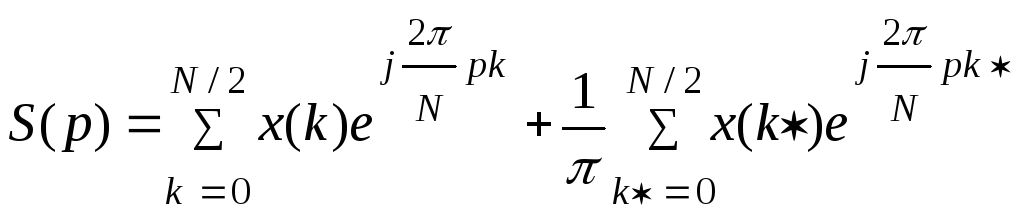 .
.