6.4.3. Матричная запись линейных корректирующих кодов
Алгебраические
коды могут представляться в матричной
форме. Существует несколько типов
матриц: образующая
,
синдромная
,
проверочная
.
Как
правило, образующая матрица имеет
размерность n×k
и состоит из k линейно
независимых разрешенных кодовых
комбинаций. Линейно независимыми
называются такие кодовые комбинации,
поразрядное суммирование которых по
модулю 2 не дает комбинацию, присутствующую
в этой матрице. Дадим еще одно определение:
вес кодовой комбинации – это количество
единиц в ней. Например, код 1011011 имеет
вес
.
Для любого корректирующего кода
минимальный вес разрешенной комбинации
не может быть меньше кодового расстояния
d, также как поразрядная
сумма любых строк образующей матрицы.
Кроме
элементарного подбора линейно независимых
кодовых комбинаций существует формальное
правило получения образующей матрицы
.
Ее можно представить в виде единичной
матрицы
и матрицы дополнения
,
причем последняя строится таким образом,
чтобы вес каждой строки был не меньше
.
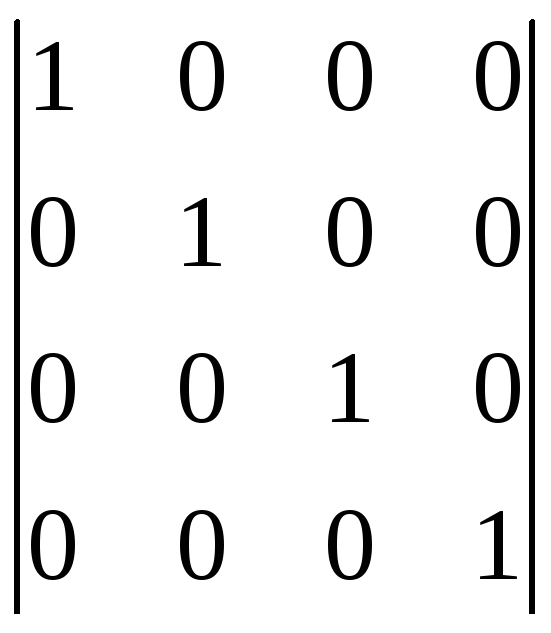
В
качестве примера используем код Хемминга
(7,4). Единичная матрица
для него имеет размерность 4×4 и
записывается в форме:
Матрица
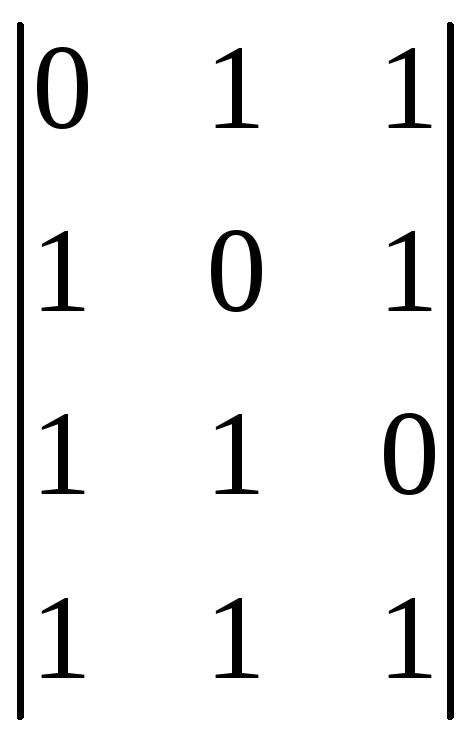
дополнения
имеет размерность 3×4 и может быть
выполнена в следующем виде:
Тогда окончательно матрица размерности 7×4 представится в виде:
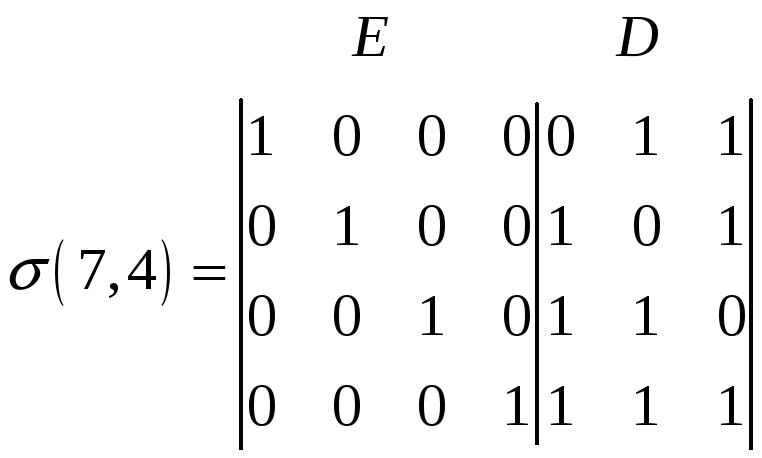
Рис. 6.36. Образующая матрица кода Хемминга (7,4)
Образующая
матрица имеет интересное свойство: и
любая ее строка, и поразрядные суммы
любых ее строк образуют разрешенные
комбинации, причем вес любой из них не
меньше
.
Проверочная
матрица кода Хемминга – это транспонированная
матрица синдромов с рис. 6.34. Она имеет
размерность
и для кода (7,4) принимает вид:
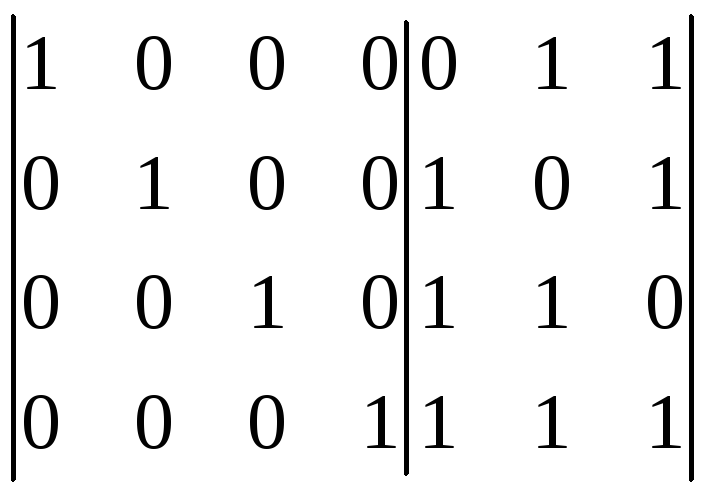
Рис. 6.37. Проверочная матрица кода Хемминга (7,4)
Обратим внимание на то, что при перестановке местами строк образующей матрицы (или ее составных подматриц) и столбцов проверочной матрицы мы можем получить эквивалентный код с теми же свойствами. Действительно, что нам стоит поменять местами синдромы ошибок по рисунку 6.34, если составить другую таблицу соответствия.
6.4.4. Коды Рида - Маллера I рода
В отличие от кодов Хемминга, являющихся не более чем академической абстракцией алгебраических кодов, коды Рида-Маллера были практически использованы в американской космонавтике.
Коды
Рида - Маллера линейны и имеют число
разрядов
,
равное степени двойки:
.
Правило кодообразования основано на
присоединении матриц
размерности
.
Рассмотрим
кодообразование для
,
т. е. при
.
Матрица нижнего уровня
содержит одну строку из 16 единиц:
=[1111111111111111].
Предположим, что один из разрядов
информационный. Тогда существует две
возможных разрешенных кодовых комбинации:
одна из них – это 16 нулей, вторая –
матрица
,
приводящая к коду с кодовым расстоянием
(код исправляет 7 ошибок мажоритарным
способом: если количество 1 больше
количества 0, он приравнивается к 1, если
наоборот – к 0).
Присоединим
следующую матрицу
,
которая представляет все четырехразрядные
коды от 0 до 15:
Рис. 6.38. Вторая матрица кода Рида-Маллера
Следующая
матрица
получается как линейная комбинация
строк предыдущей матрицы, причем в
основе лежит логическое умножение
строк. При
матрица имеет вид:
Рис. 6.39. Третья матрица кода Рида-Маллера
Если
эту матрицу подключить в качестве
образующей к предыдущей, результирующий
код имеет кодовое расстояние
и, следовательно, исправляет одиночные
ошибки.
В результате необходимо понять принцип организации кодов Рида-Маллера и их способ декодирования.
Коды Рида-Маллера на практике используются достаточно редко, так как предполагают большую избыточность по отношению к исходной информации.