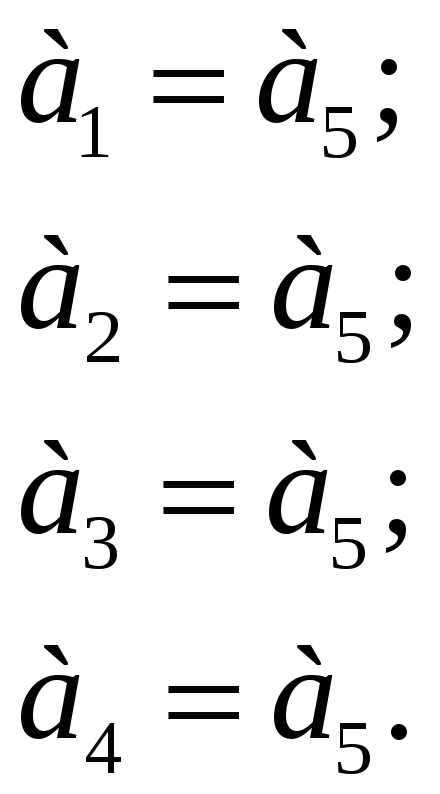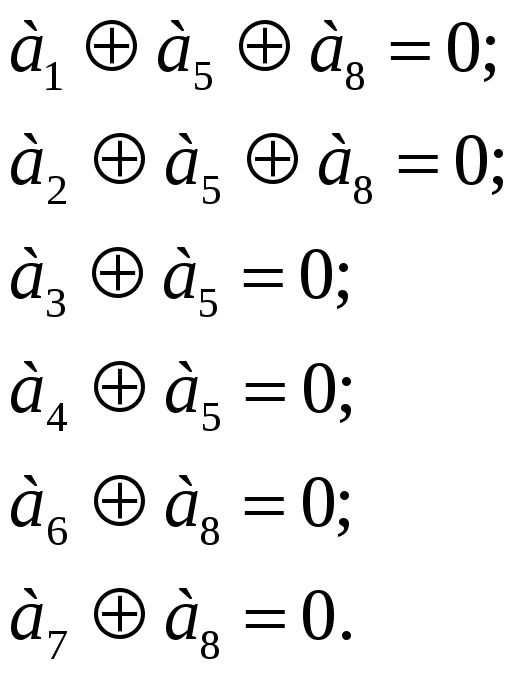6.4.2. Алгебраические коды

Коды основаны на алгебраических методах кодирования/декодирования. В большинстве случаев методы основаны на простейших операциях бинарной логики, а именно на сложении по модулю 2.

Одним из первых корректирующих кодов был предложен код Р. Хемминга. Он основан на простейшей идее: синдром ошибки является двоичным кодом номера разряда с ошибкой. Например, код синдрома 101 должен соответствовать пятому разряду с ошибкой.

Для того, чтобы это правило срабатывало, необходимо составить таблицу соответствия, в которой синдром должен однозначно определять номер разряда с ошибкой. Приведем пример для 8-разрядного кода. В этом коде (7.4) ( – общее число разрядов; – количество информационных разрядов) можно представить таблицу соответствия:

Рис. 6.28. Матричное и алгебраическое представление кода Хемминга

Справа приведена система проверочных равенств, которая реализована по следующему принципу: по каждому столбцу двоичных кодов синдромов приводятся соответствующие разряды, которые суммируются по модулю 2 и приравниваются к 0. Рассмотрим последние разряды таблицы синдромов. Разряду с единицами соответствуют , , и . Из этого вытекает первое проверочное равенство: . Аналогично реализуются и другие проверочные равенства.

Предположим, . Вычислим необходимое число контрольных разрядов: . Путем подбора получаем . Тогда.

Составляем таблицу синдромов и примыкающую к ней систему проверочных равенств (рис. 6.29).

Рис. 6.29. Матричное и алгебраическое представление кода Хемминга (13,9)

Из выражений по рис 6.28 и 6.29 можно интерпретировать код Хемминга на любое количество разрядов.

Из приведенных выражений непонятно, как назначать контрольные разряды. В принципе, они могут быть любыми. Желательно, однако, чтобы количество вычислений при кодировании и декодировании было минимальным. Для этого желательно выполнить критерий минимальной разрешимости, согласно которому из системы проверочных равенств нужно выбрать такие контрольные разряды, при которых системы уравнений становятся вырожденными. Это происходит, когда каждый член системы уравнений присутствует в ней однократно. Тогда система уравнений по рис. 6.29 преобразуется к виду:

(6.30)

В алгебре сложения по модулю 2 достаточно перенести любое количество слагаемых из одной части уравнения в другую; результат при этом не меняется.

Аналогично для второй системы проверочных равенств по рис. 6.30 получаем:

(6.31)

Из приведенных соотношений (6.30) и (6.31) вытекает следующее:

1. контрольные разряды должны соответствовать степени двойки. Таким образом, номера контрольных разрядов в дальнейшем равны а₁₆, а₃₂,…,а^2к.

2. при той же корректирующей способности увеличение общего количества разрядов приводит к положительному эффекту.

Обратимся к определению скорости кода:

(6.32)

Преобразуем выражение (6.32) к виду:

(6.33)

При этом в связи с увеличением скорость повышается с увеличением .

Контроль на четность может быть реализован как на программном, так и на аппаратном уровнях. В последнем случае структура передающей части принимает вид, приведенный на рисунке 6.31.

Рис. 6.30. Контроль на четность

Здесь элемент D1 – счетный триггер, переходящий в противоположное состояние при каждом импульсе на входе. После прохождения всего кода при четном количестве единиц на последнем разряде будет присутствовать ноль, в противном случае – единица.

Для формирования кода Хемминга в общем случае необходимы более сложные процедуры. Рассмотрим код (7,4). В реализации кода (7,4) на передающей части необходимо реализовать уравнения (6.30). Они представляются в виде структурной схемы (рис. 6.31).

Здесь схемы совпадения D1,…, D4 выделяют информационные разряды, причем разряды «подаются » задом наперед. Схема D5 объединяет информационные разряды в нужные такты. Так, первое уравнение системы (3.30) реализуется схемой D6 и D9, причем счетный триггер D9 реализует контроль на четность. Предварительно триггер D9 устанавливается в 0. Аналогично работают остальные устройства. Так, схема D7 организует второе проверочное равенство из системы (6.30).

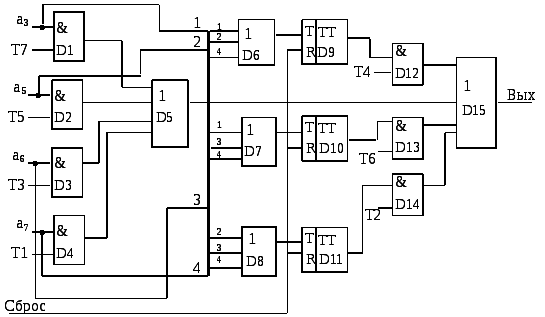
Рис. 6.31. Структура кодера Хемминга

Декодирующая система, реализующая алгоритм (6.31), может представиться в виде, представленном на рисунке 6.33.

Здесь верхняя часть схемы представляет систему приема и коррекции кода. Схемы D1,…, D4 выделяют информационные разряды, которые заносятся в буферную память на счетных триггерах D5,.., D8.

Нижняя часть устройства организует контроль на четность. Для этого на схемах D13, D14, D15 выделяются нужные такты для проверочных равенств по рисунку 3.30. Например, схема «ИЛИ» D13 формирует первое равенство ().

Схемы D16, D17, D18 выделяют единицы из принятого кода в соответствии с проверочными равенствами, а счетные триггеры D19, D20, D21 проводят контроль на четность.

В соответствии со свойствами кодов Хемминга двоичный код синдрома преобразуется в позиционный с помощью дешифратора D22. Восьмым тактом на схемах D23,…, D26 выделяется импульс коррекции (один из возможных импульсов) при наличии одиночной ошибки. Импульс коррекции поступает на С – вход соответствующего триггера D5,…, D8. В этот же такт осуществляется считывание скорректированного кода через схемы D9,…, D12.

Как видно из приведенных схем, кодирование и декодирование последовательных кодов достаточно громоздко.

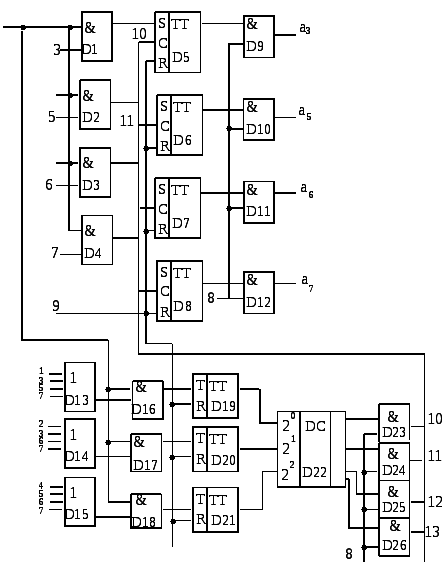
Рис. 6.32. Дешифратор кода Хемминга (7,4)

Приведем примеры кодирования и декодирования в алгебраической форме. Предположим, безызбыточный код иметь вид 1011. Эти разряды соответствуют позициям кода , , и . соответственно. Вычислим контрольные разряды в соответствии с проверочными равенствами:

Окончательно код принимает вид 0110011. Аналогично вычисляются остальные коды при 15 возможных комбинациях безызбыточного кода.

Займемся теперь приемом, причем за базу примем сформированный код. Предположим, код принят без ошибок. Тогда при приеме формируется следующий синдром:

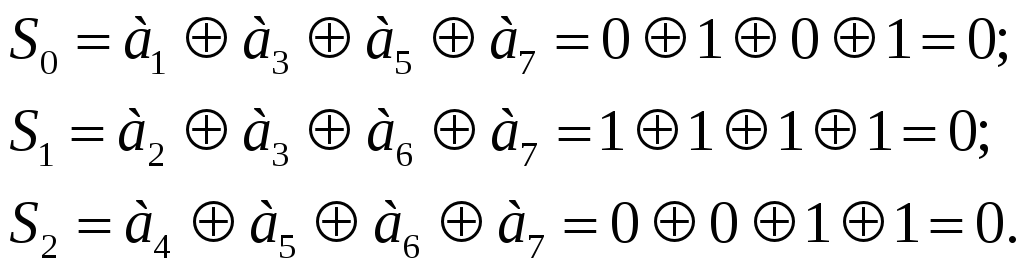
То есть, ошибки не обнаружены. Представим теперь, что произошла ошибка в разряде , т. е. код имеет вид 0110111. Вычисляем синдром:

Получим синдром, соответствующий десятичной цифре 5 – ошибка в пятом разряде исправляется.

Теперь представим, что произошла двойная ошибка, и кол принимает вид 1110111. синдром получается следующего вида:

Синдром вида 110 означает ошибку в разряде; после её исправления в коде будет уже не две, а три ошибки. Этот эффект носит название размножения ошибок и является большим недостатком корректирующих кодов: если количество ошибок превышает допустимое, при декодировании ошибки размножаются.

Коды Хемминга относятся к числу академических: они в принципе реализуемы, но неэффективны. Можно повысить их корректирующую способность, но не намного и неэффективно. В частности, существует способ повышения кодового расстояния от (классический код Хемминга) до . Для этого вводится дополнительный контрольный разряд с контролем на четность. В частности, для кодов Хемминга (7,4) вводится дополнительный 8-й разряд, который для передающей части записывается в виде:

,

(6.34)

а для приемной:

.

(6.35)

Полученный код интерпретируется достаточно просто. Он способен исправлять одиночные ошибки и обнаруживать двойные. Правило достаточно простое: если при приеме появился ненулевой синдром, а в дополнительном разряде 0, это признак двойной ошибки, и принятый код отбрасывается.

Отметим одну интересную деталь корректирующих кодов. Определим понятие совершенного кода. Код называется совершенным, если он при заданной корректирующей способности и заданном количестве информационных разрядов способен обеспечить максимальную скорость . В частности, для кодов Хемминга совершенными являются коды, реализующие в полной мере правило (6.28), т. е. максимальное разрешение по синдромам. Для кодов Хемминга это коды (7,4), (15,11), (31,26) и т.д. Обратите внимание, что первая цифра – (т. е. максимальное количество синдромов при заданном количестве разрядов), вторая – максимально возможное при этом значение . Дальнейшие совершенные коды – это (63,57), (127,120) и т.д. Проявляется ранее оговоренный эффект повышения скорости при заданной корректирующей способности кода. Это абстрактно-математическая постановка задачи, при которой бесконечное удлинение кода приводит к скорости, приближающейся к 1. Фактически срабатывают другие факторы, сводящиеся к следующему: чем длиннее код, тем больше вероятность «подхватить» ошибки большей кратности. В частности, на этом принципе основаны технологии АТМ высокоскоростной передачи данных и оперирующие со сравнительно короткими кодовыми блоками.

Более сложные алгоритмы кодирования/декодирования алгебраических кодов включают усложненную обработку кодов. В качестве примера рассмотрим мажоритарное кодирование/декодирование. В качестве примера рассмотрим коды, исправляющие двойные ошибки. При жестком (синдромном) декодировании обязательное условие – однозначность.

Рассмотрим в качестве примера алгебраические (синдромные) коды с кодовым расстоянием (т. е. исправляющие двойные ошибки). Для достижения этого качества подбираются синдромы ошибок, причем в простейшем варианте подбор делается с помощью тривиального перебора. Методику лучше рассмотреть на примере. Формируем синдромы ошибок по критерию однозначности. Первые два синдрома, а именно 00…001 и 00…010 проходят однозначно, так как они свидетельствуют о наличии одиночных ошибок в первом и втором разрядах. Третий синдром 000…011 теряет свойство однозначности, так как он по правилам кодообразования может быть индикатором ошибки в третьем разряде или двойной ошибки в первом и втором разрядах. Следовательно, такой синдром не может быть использован. Аналогично проверяются другие возможные синдромы. В результате для первых 8 разрядов корректирующего кода, исправляющего двойные ошибки, таблица синдромов приобретает вид, приведенный на рисунке 6.33.

Рис. 6.33. Таблица синдромов

Отметим особенность: синдром, содержащий единственную единицу, является признаком контрольного разряда. Следовательно, на рассматриваемом множестве синдромов информационными могут быть только разряда а₅ и а₈. Первый код имеет размерность (5,1), второй – (8,2). Код (5,1) формируется только из единственного контрольного разряда, следовательно, включает две разрешенные кодовых комбинации, при и .

Запишем систему проверочных равенств по тем же принципам, что и для кодов Хемминга: уравнения формируются по столбцам и включаются только те разряды, в которых присутствуют единицы синдромы. Так, для «младшего» разряда получим: или . Продолжая эту методику, получим следующую систему проверочных равенств:

(6.36)

Согласно системе уравнений (6.36) существует две разрешенные кодовые комбинации, с кодами 00000 и 11111. Понятно, что кодовое расстояние между ними равно 5, а принцип декодирования тривиален: если в принятом коде единиц больше, чем нулей, следовательно, передавалась 1, если меньше – 0.

Более сложным представляется вариант 2, соответствующий коду (8,2) и имеющий следующую систему равенств:

(6.37)

Полученный код имеет уже три ненулевых разрешенных кодовых комбинаций. «Играем» от информационных разрядов, имеющих коды 01, 10 и 11. Соответствующие разрешенные кодовые комбинации имеют вид:

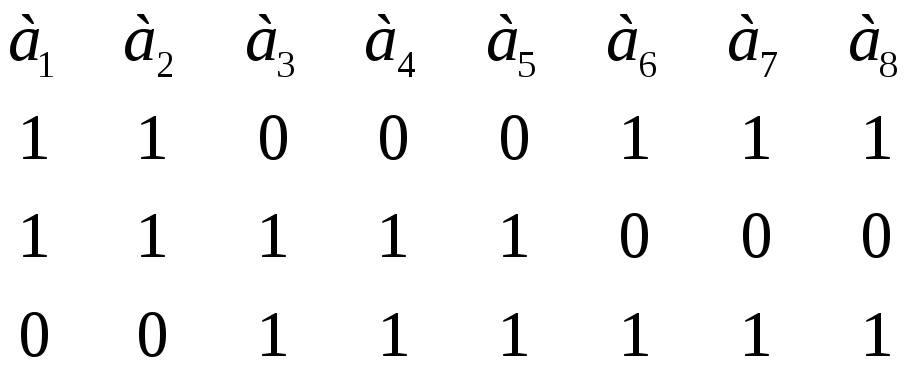
Рис. 6.34. Разрешенные кодовые комбинации

Рис. 6.35. Таблица синдромов для кодов, исправляющих двойные ошибки

В результате кодовое расстояние не меньше 5. Аналогичные выражения можно получить для кодов большей длины. В частности, можно продолжить таблицу по рисунку 6.34 для большего числа разрядов. Таблица соответствующих синдромов приведена на рисунке 6.35.

Из таблицы видно, что с увеличением скорость повышается, так как количество информационных разрядов возрастает. Так, следующим информационным разрядом является (код (10,4)), (код (11,5)), (код (13,6)), (код (14,7)) и (код (15, 8)). Это направление в наше время достаточно перспективно для любой корректирующей способности кода, если составить программу вычисления синдромов.
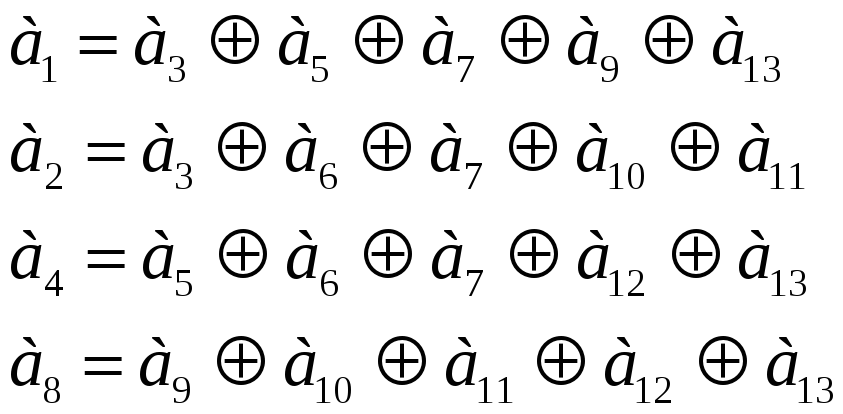
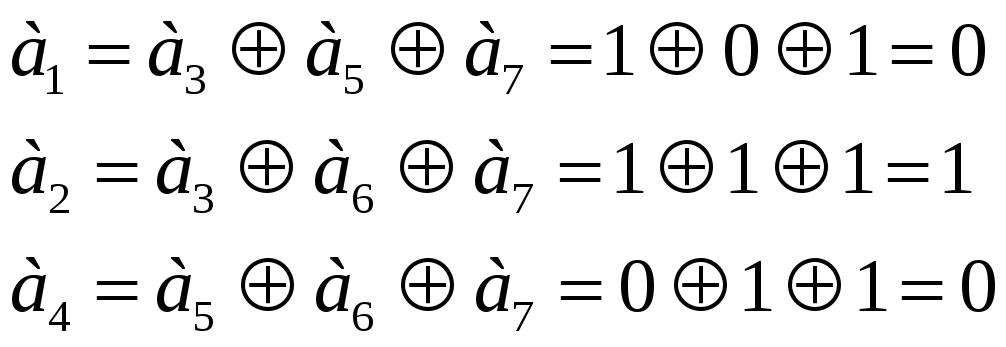
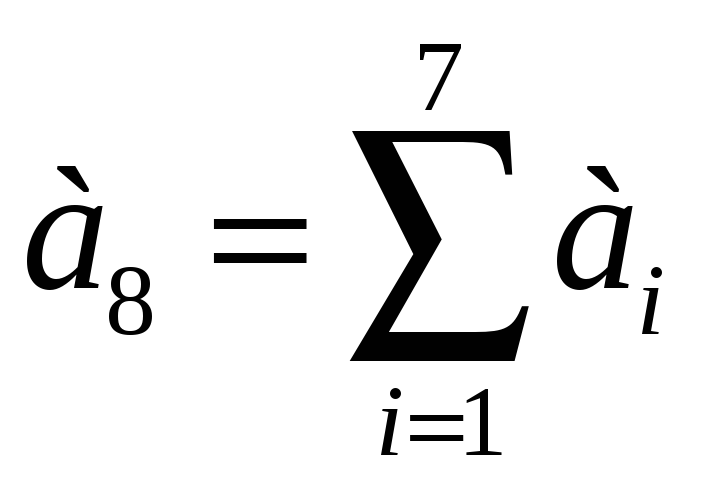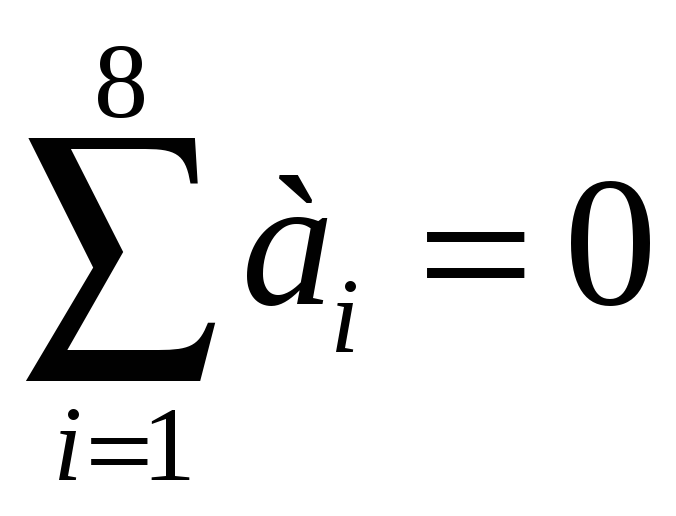