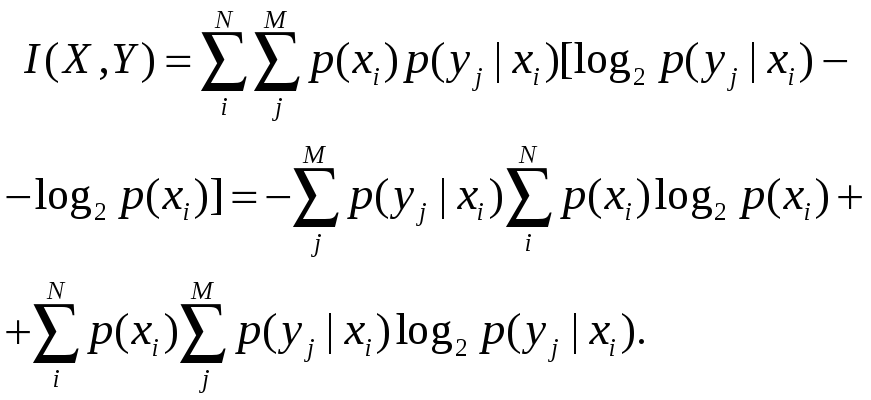1.3. Теория информации
Основополагающей в области теории информации является работа Шеннона [47], в которой введены количественные оценки и получены основные соотношения.
Согласно
Шеннону, основным фактором, определяющим
возникновение и передачу информации,
является неопределённость источника
(см. рис.1.1). Источник последовательно
во времени может принимать одно из
состояний, причём эти состояния в
идеальном случае заранее непредсказуемы.
Если наблюдение за состояниями источника
идёт достаточно долго, можно вычислить
относительные частоты их появления:
.
Здесь
– общее количество различных состояний
за время наблюдения;
– количество состояний
.
Обычно принимают, что источник
эргодический: это означает, что при
неограниченном увеличении
относительные частоты появления
состояний стремятся к их вероятностям:
|
|
(1.88) |
.
Под состоянием источника понимается, например, буква некоторого алфавита на его выходе. За меру неопределённости источника К. Шеннон принял логарифмическую функцию. Она обладает следующими особенностями:
-
равна нулю при
,
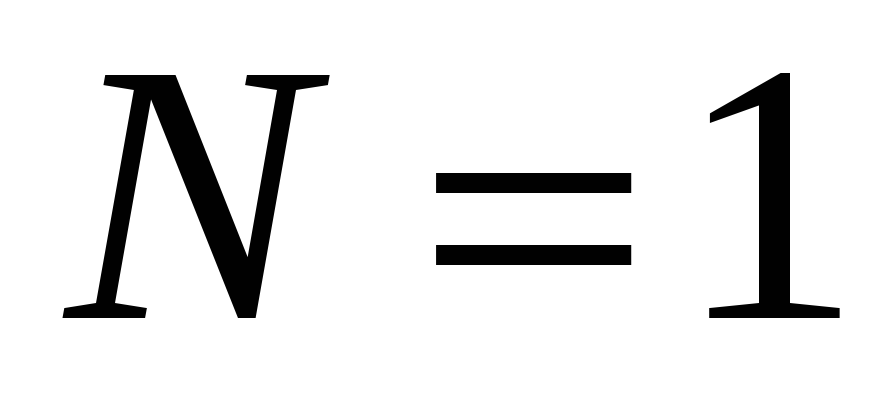т. е. при достоверном состоянии источника -
монотонно возрастает с увеличением
; -
неотрицательна при
; -
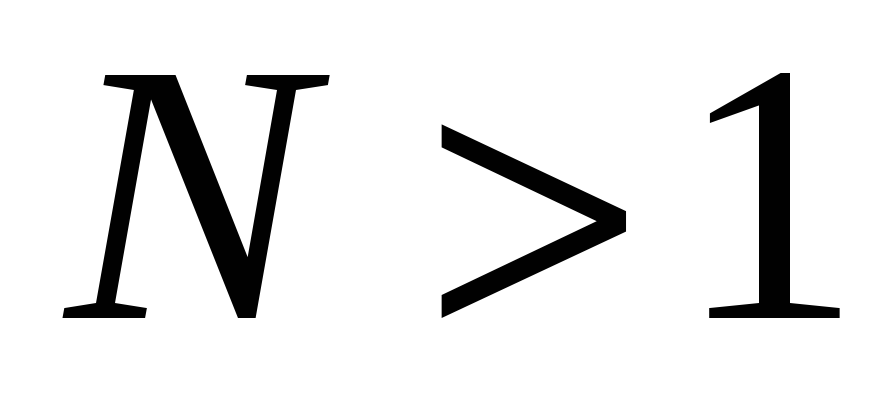общая неопределённость совокупности нескольких источников равна сумме их неопределённостей.
Мера
неопределённости была названа энтропией.
Название взято из термодинамики, в
которой она характеризовала рассеяние
(хаотичность) энергии. Согласно определению
Шеннона, энтропия источника
определяется выражением:
|
|
(1.89) |
.
В выражении (1.89) логарифм по основанию 2 был взят из соображений источника с минимальным числом различных состояний. В этом случае энтропия измеряется в битах.
Оценим свойства полученной характеристики.
1.
неотрицательная величина, поскольку
вероятность
всегда неотрицательна, а логарифм числа,
меньшего 1, всегда отрицателен.
2.Энтропия
при заданном
максимальна при равновероятных состояниях
источника. В этом случае она может
задаваться по формуле, предложенной
Р.Хартли:
|
|
(1.90) |
.
3.
С увеличением числа различных состояний
энтропия возрастает.
4.Маловероятные события при вычислении по формуле (1.89) могут не учитываться. Это объясняется тем, что
.
Для дальнейшего изложения необходимо ввести ещё две величины. Это, во-первых, полная энтропия, которая может рассматриваться как совместная неопределённость ансамбля из двух независимых источников:
|
|
(1.91) |
.Здесь
и
– количество различных состояний
и
.
Предположим вначале, что источники независимы. Тогда на основе формулы произведения вероятностей можно записать:
,
а (1.91) трансформируется к виду:
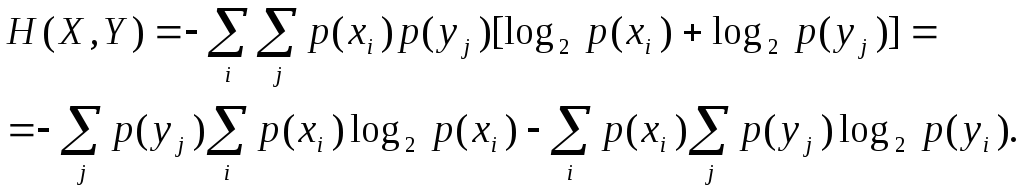
Поскольку
(вероятность полной группы событий),
окончательно имеем:
|
|
(1.92) |
,
то есть, энтропия ансамбля из двух независимых источников равна сумме их энтропий.
Предположим теперь, что источники зависимы. Тогда, согласно формуле Байеса
|
|
(1.93) |
,
где
и
– условные вероятности. Подставим
(1.93) в (1.91):
|
|
(1.94) |
В
выражении (1.94)
(полная группа событий); тогда первый
член представляет энтропию
.
Во втром члене сумма
называется частной условной энтропией
(неопределённостью состояния
относительно совершившегося состояния
),
а вся сумма представляет собой
математическое ожидание частных условных
энтропией и называется условной
энтропией:
|
|
(1.95) |
.
Тогда окончательно выражение (1.93) примет вид:
|
|
(1.96) |
.
Сравнивая между собой полные энтропии, вычисленные по формулам (1.92) и (1.96), отметим, что в первом случае она больше, чем во втором (энтропия ансамбля источников при их взаимной зависимости снижается), а это значит, что
|
|
(1.97) |
.
Если расписать формулу Байеса наоборот,
|
|
|
,
то с помощью аналогичных преобразований получим
|
|
(1.98) |
.На основании введённых понятий можно ввести определение количества информации. Обратимся к простейшей модели передачи информации, изображённой на рис. 1.16.
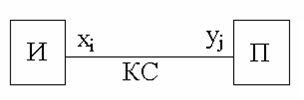
Рис. 1.16. Модель передачи информации
В
ней источник вырабатывает сообщения
,
а приёмник по ним восстанавливает
символы
(в общем случае
).
При передаче одного символа неопределенность
источника снижается на величину
|
|
(1.99) |
,
где
– количество информации, полученное
при приёме
.
Просуммируем все возможные состояния с учетом их вероятностей:
|
|
(1.100) |
.
Применим формулу Байеса:
|
|
(1.101) |
Второй
член в (1.101), в соответствии с (1.95), равен
условной энтропии
.
Поскольку
,
окончательно из (1.101)
|
|
(1.102) |
.
Поскольку формулу Байеса можно написать в симметричной форме, получим формулу:
|
|
(1.103) |
,
Теперь, выразив из (1.96) условную энтропию и подставив в (1.103), получаем:
|
|
(1.104) |
.
Отметим,
прежде всего, что и энтропию источника
(выражение (1.89)), и полную энтропию (1.91),
и количество информации (1.100) можно
трактовать как математическое ожидание,
приходящееся на один символ. В первом
случае это среднее значение частной
энтропии
,
во втором – частной совместной энтропии
–
,
в третьем – частного количества
информации
.
Второе, не менее важное свойство количества информации – симметричность передачи информации. Выражение (1.102) задает количество информации относительно источника, (1.103) относительно приёмника, а (1.104) относительно всего информационного канала. Вследствие этого количество информации – величина скалярная. Кроме этого, указанное свойство требует учитывать свойства всего канала целиком. Например, источник может увеличить скорость передачи сообщений, но если она недопустима для линии связи (ограничение частотного диапазона) или приёмника (ограничение скорости декодирования), количество информации на символ даже уменьшится, поскольку не все символы сообщения восстановятся приёмником.
Сделаем
количественную оценку
.
1.
.
Это вытекает из соотношений (1.102) и
(1.97).
2.
Количество информации минимально, если
и
никак не связаны. В этом случае
и из (1.102)
.
Это свойство легко интерпретируется
практически: если вам что-то говорят на
незнакомом вам языке, информацию вы не
получаете.
3.
Информация максимальна, если
:
.
Это позволяет определить энтропию
источника как максимальное количество
информации, которое можно от него
получить. В свою очередь, из свойств 2 и
3 условная энтропия приобретает смысл
потерь информации.
Определим
теперь количество информации непрерывных
сообщений. Пример источника непрерывных
сообщений – объект, один из параметров
которого нужно измерить (например,
температуру, давление, скорость и т.д.).
На первый взгляд может показаться, что
такие источники могут иметь бесконечную
энтропию даже в ограниченном диапазоне.
Фактически любая процедура получения
информации от такого источника (она
называется измерением) имеет погрешность.
Погрешность вызывается неточностью
измерителя и флуктуациями самого
параметра. Примем, что в диапазоне
изменения величины
измерение происходит с абсолютной
погрешностью
.
Тогда мы условно можем выделить
дискретных состояний с шагом
(или квантов), а энтропия при условии
равновероятных состояний
|
|
(1.105) |
.
Эта
формула аналогична энтропии по Хартли
(1.90). Из неё видно, что увеличение точности
измерения (снижение
)
повышает количество информации от
источника.
Более
точное выражение для количества
информации с учетом распределения
вероятности величины
определено К. Шенноном. Если предположить,
что
– измеряемый физический параметр, а
– результат измерения, то количество
информации в одном измерении:
|
|
(1.106) |
.
Здесь
– двумерная плотность распределения.
Применим формулу Байеса:
|
|
(1.107) |
,
где
– условная плотность распределения.
Подставим (1.107) в (1.106):
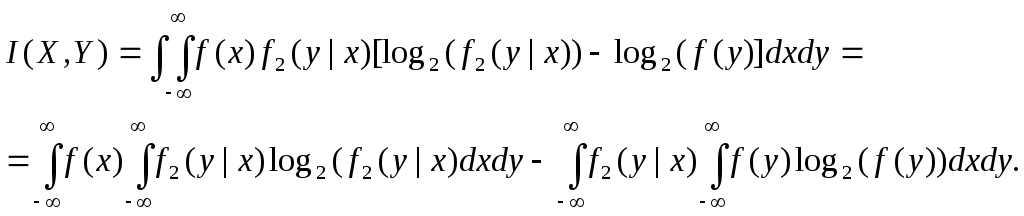
Поскольку
(условие нормировки), получим
|
|
(1.108) |
.
Получили выражение, тождественное (1.103) для дискретных сигналов, только в нём энтропии вычисляются по-другому:
|
|
(1.109) |
|
|
(1.110) |
;
.
Аналогично
запишутся выражения для
и
:
|
|
(1.111) |
|
|
(1.112) |
;
.
Приведём примеры.
1.
Оценим информационную ёмкость русского
алфавита. Предположим, что при передаче
русского текста буквы е и ё не различаются.
Тогда в алфавите останется 32 буквы. Если
бы они в тексте встречались с одинаковыми
вероятностями, энтропия одной буквы
составила бы
бит. Фактически вероятности разные; с
учетом разных вероятностей букв
(полученных эмпирически) энтропия буквы
снижается до 3,2 бит. Кроме этого, в тексте
символы имеют взаимосвязь с соседними
(например, буквы ь и ъ не могут стоять
после гласных, а жи- и ши- пишутся с буквой
и), что ещё больше снижает энтропию. Она
уменьшается (или варьируется в некоторых
пределах) в зависимости от характера
текста, его автора и т.д. и практически
лежит в пределах (2-2,7) бит [1.18].
2. Энтропия двоичного безызбыточного кода равна 1 бит на разряд при условии равновероятных значений 0 и 1. Для несимметричных каналов с разными вероятностями искажения 0 и 1 пытаются изменить вероятности этих символов; при этом энтропия снижается. Энтропия меньше и у корректирующих кодов, где часть разрядов информацию не несёт. Наконец, при использовании двоично-десятичных кодов также появляется избыточность, так как из 16 различных четырёхразрядных кодовых комбинаций используется только 10.
3.
Оценим энтропию источника непрерывных
сообщений с равномерно распределённым
физическим параметром в интервале
и с погрешностью измерения
.
Предположим, погрешность неизменна во
всем диапазоне измерения.
Тогда
;
и формула (1.106) преобразуется к виду:
.
Полученный
результат совпадает с (1.105). Отметим
попутно, что равномерное распределение
измеряемой величины даёт наибольшее
количество информации: при любом другом
распределении количество информации
уменьшается. Обратное явление будет
для распределения
:
отличие распределения от равномерного
повышает количество информации.
Введём в рассмотрение динамические параметры передачи информации. Одна из основных динамических характеристик – скорость передачи, или поток информации. Это количество информации, вырабатываемое источником в единицу времени:
|
|
(1.113) |
.
Единица
измерения потока – бит/с или бод. Если,
например, информация передаётся двоичным
кодом с периодом следования импульсов
,
то поток информации
(бод). В выражении (1.113)
называется потоком условной энтропии.
Н
,
часть которого
теряется в информационном канале,
поэтому приёмнику «достаётся» только
разность, которая и определяет поток
информации.
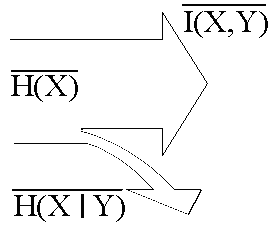
Рис. 1.17. Диаграмма распределения потоков информации
Кроме потока информации обычно задаётся пропускная способность. Пропускная способность информационного канала – это максимально допустимый поток информации в нём:
|
|
(1.114) |
.Обозначения символов в информационном канале взяты из рис. 1.1. Аналогично можно определить пропускную способность канала связи:
|
|
(1.115) |
.
Очевидно,
.
Отметим факторы, ограничивающие
пропускную способность, при условии,
что поток энтропии источника не ограничен.
1.
Ограниченный частотный диапазон канала
связи. Если принять, что сообщения
передаются прямоугольными импульсами
периода
со скважностью 2, то из (1.28) известно, что
частотный диапазон этих импульсов
.
Отсюда для обеспечения потока информации
требуется частотный диапазон
.
Фактически он меньше, потому что при
приёме импульсов достаточно различить
два уровня: 0 и 1. Но минимально допустимая
полоса частот при этом
.
Это и есть предельная оценка потока
информации.
2. Наличие избыточности сообщений. Об избыточности русскоязычного текста уже говорилось; то же самое можно вывести и для других сообщений. Избыточность, кроме того, возникает при передаче корректирующими кодами, а также при передаче служебных импульсов (стартовых, протокольных, синхронизации т.д.).
К. Шеннон сформулировал и доказал ряд теорем [47] суть которых сводится к следующему: при наличии запаса по пропускной способности информационного канала можно найти способ передачи, позволяющей передать без искажений все сообщения при любом уровне помех в канале. Эти теоремы являются фундаментальными при разработке методов помехоустойчивого приёма. В принципе, они тавтологичны (т. е. формулируются одинаково). В качестве примера приведем две теоремы Шеннона для дискретных каналов с шумами.
Прямая
теорема. Если пропускная способность
информационной системы
равна:
,
где
– бесконечно малая величина, то существует
способ передачи, при котором можно
передать все сообщения без искажений.
Обратная
теорема. Если пропускная способность
,
то не существует способа передачи,
гарантирующего отсутствие искажений.
В заключение приведём важное соотношение. Если амплитуды полезного сигнала распределены по нормальному закону, а помеха – белый шум, то пропускная способность
|
|
(1.116) |
,
где
– полоса частот полезного сигнала;
,
– мощности сигнала и шума соответственно.
Приведём пример. Акустический сигнал (телефонный разговор) достаточно передавать с частотой 8 кГц. Если амплитуды сообщений передаются 8-разрядным кодом (1 байт), скорость передачи информации 64 кбод.
Контрольные вопросы
1) Поясните, почему в качестве меры неопределенности выбрана функция логарифма.
2) Чем энтропия по Хартли отличается от энтропии по Шеннону?
3) Назовите и объясните свойства энтропии. Когда она максимальна?
4) Когда максимальна полная энтропия?
5) Поясните смысл условной энтропии.
6) Поясните смысл выражения для количества информации.
7) Сформулируйте свойства количества информации и поясните их практический смысл.
8) Что такое эргодическая последовательность символов?
9) Для чего вводятся понятия поток информации и поток энтропии?
10) Как оценивается энтропия непрерывных сообщений?
11) Что такое избыточность информационных сообщений? Для чего она вводится?
12) Каков смысл теорем Шеннона для каналов связи? Поясните их на примерах.
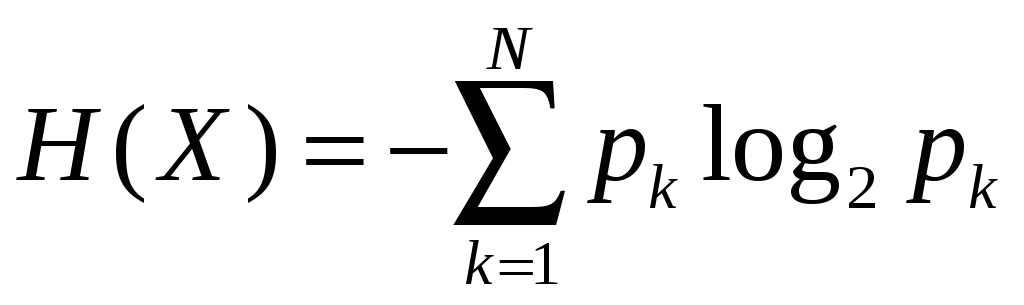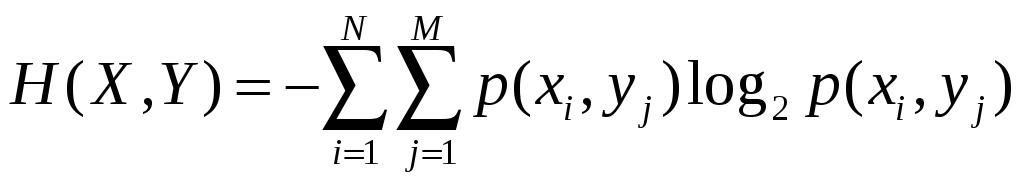