6.5.2 Сверточное кодирование

Это тоже непрерывные коды, но они достаточно продуктивно используются в радиоканалах. Их особенностью является то, что в них не выделяются отдельно информационные и контрольные разряды, а формируются два отдельных потока, которые потом поочередно коммутируются. В качестве производящих составляющих обычно используются полиномиальные коды, в частности умножения на образующий полином. Структурная схема кодера имеет вид, приведенный на рисунке 6.68.

Рис. 6.67. Структура кодера сверточного кода

Здесь обозначено: СУ1, СУ2 – схемы умножения на образующий полином; СК – синхронный коммутатор.

Обычно при сверточном кодировании в качестве образующих выбирают полиномы взаимно простые (не делящиеся друг на друга нацело и не имеющие общих полиномов разложения на нижние степени). Если принять, что при входном потоке возможно выделение разрядов, относительно каждой ветви преобразования допустимо определение кодового расстояния и предположить, что по верхней цепи преобразования кодовое расстояние равно , а по нижней – , тогда результирующее кодовое расстояние при условии независимости образующих полиномов запишется в виде:

.

(6.60)

Благодаря этому, при сравнительно незначительных затратах на аппаратную часть и небольшое время задержки, можно обеспечить достаточно высокую помехоустойчивость.

6.5.3. Каскадные коды

Каскадное кодирование предполагает последовательную процедуру использования различных методов кодирования/декодирования. Наиболее популярный пример – совместное использование кодов БЧХ и Рида-Соломона (РС). Структура алгоритма приведена на рисунке 6.68.

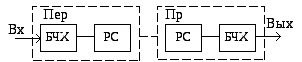
Рис. 6.68. Структура каскадного кодирования

Здесь обозначено: Пер – передающая, Пр – приемная часть системы.

Несмотря на кажущуюся простоту, алгоритм каскадного кодирования имеет серьезные ограничения. Не всякое сочетание корректирующих кодов дает высокий положительный эффект. В приведенном примере достаточно, чтобы в полиномиальном коде (в данном случае коде БЧХ) и в коде Рида-Соломона не должно быть общих сомножителей. Особенно хороший эффект обеспечивает взаимное несоответствие оснований кодов.

Недостаток каскадных кодов – задержки в обработке сигналов. Несмотря на то, что результирующее кодовое расстояние равно произведению составляющих кодовых расстояний кодов, каскадные коды не обеспечивают достаточного эффекта. Это связано с понижением корректирующей способности на этапах согласования кодов, а также согласования алгоритмов на различных алгебраических принципах.

6.5.4. Нелинейные коды

Нелинейными называются коды, не подчиняющиеся математическим преобразованиям, но обеспечивающие максимальную корректирующую способность при заданных ограничениях. Один из наиболее простых алгоритмов нелинейных кодов – коды с постоянным весом (КПВ). Напомним, что весом называется количество единиц в блочном коде. Из пространства кодовых комбинаций возможно достаточно большое количество решений, особенно если исходная методика кодирования совпадает с некоторыми критериями. Один из таких критериев – коды с постоянным весом (КПВ). В них на блок с n разрядами должно всегда присутствовать ровно единиц.

Оценим мощность КПВ. Для этого сопоставим количество возможных ошибок кратности -разрядного двоичного кода как :

.

(6.61)

Вторая оценка – количество возможных разрешенных КК. Для комбинаций с постоянным весом:

,

(6.62)

где – количество единиц, т. е. вес кода.

Коды с постоянным весом являются достаточно мощными, но ограниченными сверху. Из множества не все комбинации могут быть включены в разрешенные: необходимо дополнительно, чтобы обеспечивалось минимальное кодовое расстояние . Это возможно, если , причем желательно, чтобы (при этом возможно наибольшее количество сочетаний).

Разрешенные коды с учетом перечисленных ограничений лучше выбирать методом прямого перебора. Алгоритм тривиален, но результат зависит от выбора первого кода. При этом получается новое определение: класс эквивалентных кодов с заданными свойствами (в данном случае это , , , ). Такие классы могут быть реализованы и для других корректирующих кодов.

В завершение этого раздела приведем полезное выражение для оценки вероятности ошибки корректирующего кода. Обозначим вероятность одиночной ошибки через р. Тогда в соответствии с формулами теории вероятности, вероятность безошибочного приема . Примем также гипотезу о независимости ошибок. Теперь, если оценивать вероятность ошибки кратности , то по формуле Байеса:

.

(6.63)

Общее количество кратности оценивается по правилам комбинаторики как . Тогда вероятность ошибки определяется как:

.

(6.64)

Это очень важная формула из области кодирования. Поскольку на практике , ее можно слегка упростить из соображений высокого затухания:

(6.65)

Приведем пример. Используется код Хэмминга (7,4) с кодовым расстоянием , вероятность одиночной ошибки (это завышенная оценка, т. к. на практике по стандарту ). Вероятность искажения кода . В принципе это оптимистическая оценка, т.к. ошибки зависят друг от друга, и конечный результат больше.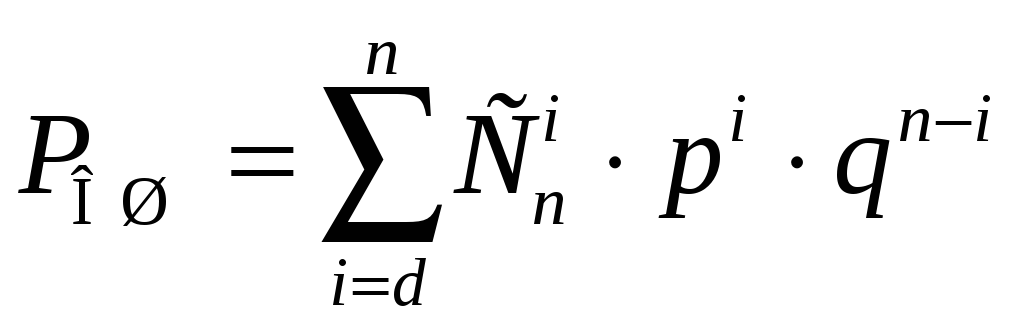