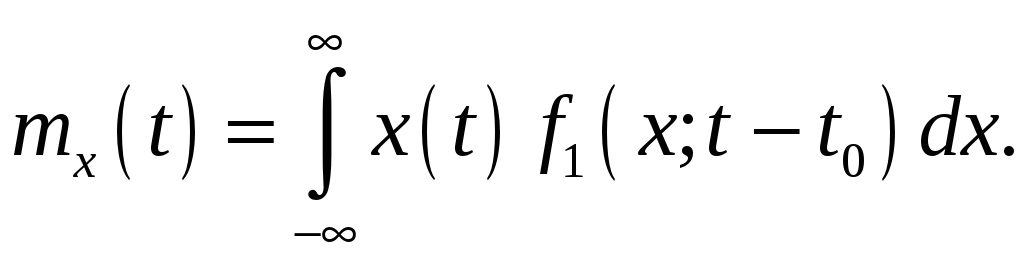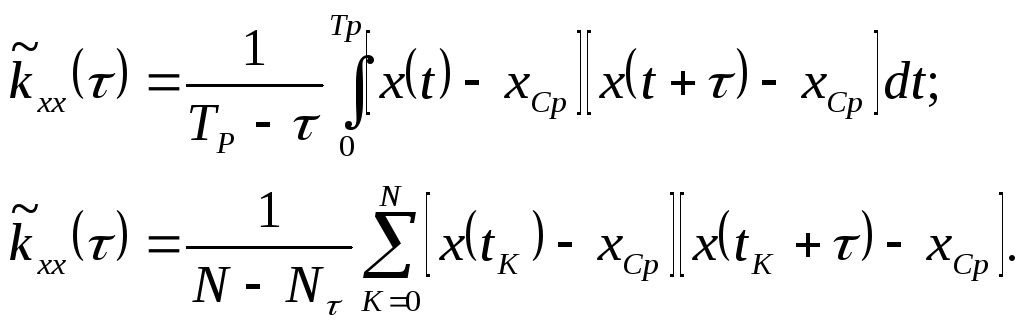4.2 Основы теории случайных процессов

Как говорилось ранее, математический термин «случайная функция» в инженерной практике заменяется определением «случайный процесс», в котором одним из аргументов является время. В наиболее простом случае имеем функцию, для которой значения определяются случайно:

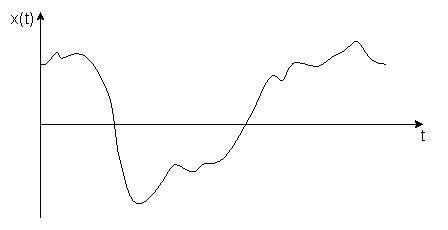
Рис. 4.16. Пример случайного процесса

В практической жизни большинство событий обладает свойствами случайного процесса. Можно использовать следующие примеры.

1. Климат и изменения температуры, давления, направления и скорости ветра.

2. Движение поезда (скорость) в реальных условиях с учётом сезона, профиля пути, атмосферных явлений, типа и веса поезда, действий локомотивной бригады и ограничений на движение.

3. Технологический процесс в промышленности (выплавка чугуна или стали, нефтеперегонные процессы, сборка технических систем на конвейере и т.д.).

4. Ситуация дорожного движения при наличии состояния дороги, светофорной политики, плотности движения, климата, времени суток.

5. Состояние живого организма (температура, давление, реакция на внешние факторы, восприятие окружающей среды) как функция времени.

Этот перечень можно продолжать достаточно долго, но даже из него можно сделать вывод о случайности всех событий в нашем физическом мире.

Строго кибернетический подход заключается в следующем. Существует некоторый физический объект, так называемый «черный ящик», за которым производится наблюдение (см. рис.4.1). Поведение этого объекта во времени представляет случайный процесс, причем объекты могут иметь непрерывный и дискретный характер. В частности, скорость автомобиля или температура живого существа непрерывны, а состояние реле в этом автомобиле или передача дискретных сигналов дискретны.

Примеры двух вариантов случайных процессов приведены на рис. 4.17. Здесь вариант а) соответствует непрерывному изменению процесса, при котором множество значений континуально (т. е. бесконечно), а вариант б) дискретен: количество значений амплитуд конечно, а случайны – моменты перехода из одного состояния в другое.

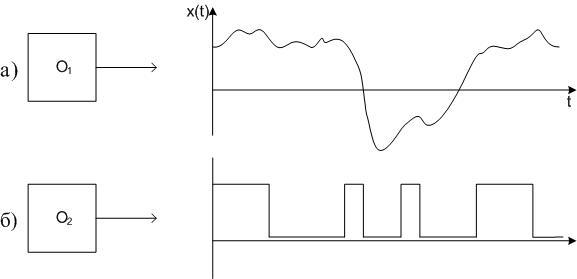
Рис. 4.17. Варианты непрерывного (а) и дискретного (б) случайных процессов

При классическом подходе считается, что существует одинаковых объектов, над которыми одновременно проводят наблюдения. Это иллюстрируется рис.4.18.

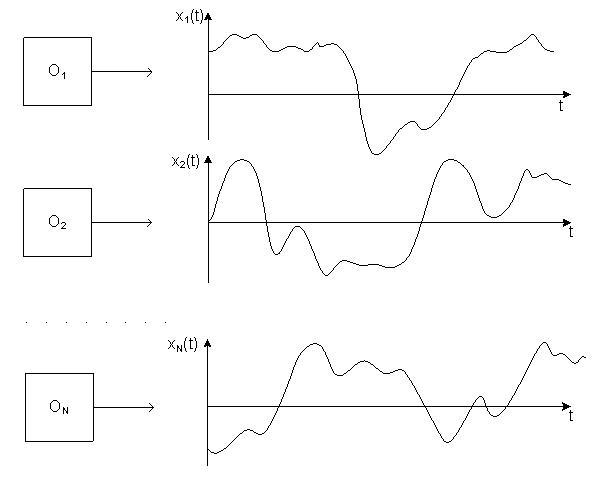
Рис. 4.18. Иллюстрация ансамбля реализаций

В результате образуется так называемый ансамбль реализаций – совокупность случайных процессов, рассматриваемых в одних амплитудных и временных интервалах. Пример ансамбля реализации случайного процесса приведен на рис. 4.19.

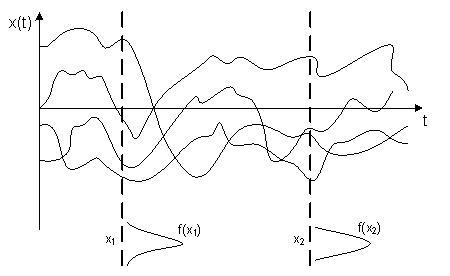
Рис. 4.19. Ансамбль реализаций

Рассмотрим определение временного сечения. Для этого достаточно зафиксировать числовые значения всех реализаций в момент времени . На рис. 4.19 показаны два сечения, в моменты и . При этом в каждом сечении образуется набор числовых данных, представляющих собой случайную величину. Она характеризуется одномерной плотностью распределения вероятностей , как это показано на рис. 4.19 в сечениях и . Отсюда следуют выводы.

1. Случайные процессы есть обобщения случайных величин введением дополнительной координаты .

2. Все свойства случайных величин в любом сечении переносятся на случайные процессы. В частности, справедливы условия нормировки, положительной определенности, ограниченности по амплитуде и интервалу.

Если плавно изменять аргумент и в каждом его значении строить плотность распределения, то можно получить так называемый цилиндр распределения – поверхность, напоминающую желоб, протяженный вдоль оси времени. Она в принципе может представляться в трехмерном пространстве в виде желоба. В самом идеальном случае желоб сохраняет форму в любом сечении; фактически картина распределения меняется в функции времени.

Хорошая аналогия однородного (стационарного) случайного процесса может быть представлена на модели рельса. Представим, что мы движемся вдоль железной дороги и на каждой случайной остановке распиливаем рельс. В каждом сечении в идеале мы получаем один и тот же профиль сечения, но даже и в этом случае только в идеале. В ходе эксплуатации рельсы изнашиваются, в том числе в зависимости от профиля пути (повороты, подъемы, спуски).

В результате, хоть и незначительно, сечения изменяют форму. Кроме того, появляется зависимость изменения формы от расстояния. Скажем, на поворотах значения износа рельса связаны между собой. Такая зависимость называется корреляцией.

Для введения дополнительного фактора взаимосвязанности двух соседних во времени распределений вводится двумерная плотность распределения вероятностей , которая является функцией четырех аргументов в пятимерном пространстве. Это чисто математический подход, согласно которому, по методу индукций, можно последовательно увеличивать мерность этой функции. Согласно логике идеальных математиков, мерность функции увеличивается до величины , причем желательно, чтобы .

Понятно, что на практике это невозможно. Тем не менее, на таком обобщении можно продемонстрировать общие свойства и обнаружить новые.

Общие:

1. Нормировка:

.

(4.34)

Тем не менее, это свойство практически интерпретируется достаточно понятно: достоверное событие имеет вероятность 1, а сколько параметров там включено, в принципе неважно.

2. Положительная определенность:

.

(4.35)

Символ называется «квантор общности» и означает «для любого из параметров». Это свойство в принципе вытекает из рассмотренного ранее, а также опирается на доказательство методом от противного. Если бы оно не выполнялось, то возможны были бы отрицательные вероятности, что противоречит определению.

3. Ограниченность по интервалу:

.

(4.36)

Свойство вытекает из условия нормировки и утверждает, что плотность распределения ограничена по любому измерению.

4. Ограниченность по амплитуде:

.

(4.37)

В противном случае нарушается условие нормировки.

Новое свойство: согласованность. Многомерную плотность распределения можно уменьшить по размерности с использованием условных вероятностей. Наиболее просто это воспринимается на примере двумерной плотности распределения:

(4.38)

В принципе, выражение (4.38) – перенос классической формулы Байеса во временную область.

Наряду с плотностями распределения существуют и количественные оценки случайных процессов, рассматриваемые ранее в теории случайных величин. В отличие от величин, они приобретают дополнительный аргумент – время . В частности, математическое ожидание в такой интерпретации есть функция времени:

(4.39)

Аналогично с дисперсией. Как было ранее определено, дисперсия – это мера отклонения случайной величины от среднего значения. В отличие от формулы (4.21) появляется дополнительный аргумент – время:

(4.40)

Следуя общему принципу, задачу желательно упрощать. Для упрощения ввели понятие стационарных случайных процессов.

При определении свойств стационарности используют два подхода. Первый называется стационарным в узком смысле и определяется следующим образом: процессы называются стационарными, если плотности распределения вероятностей для них не зависят от выбора начального отсчета:

(4.41)

Применительно к примеру о трубе (рельсе), где бы мы ни разрезали, мы получим тот же профиль.

Применим свойство стационарности к математическому ожиданию:

(4.42)

Согласно общему определению, можно принять . Тогда получим, что математическое ожидание не зависит от времени, так как плотность распределения так же от него не зависит:

(4.43)

Аналогичные рассуждения справедливы и для дисперсии. Так как двумерная плотность распределения превращается в одномерную, то выражение (4.40) приобретает форму:

(4.44)

т. е. дисперсия не зависит от времени.

Еще одна очень полезная характеристика – центральный смешанный момент второго порядка, или корреляционная функция:

(4.45)

Согласно определению стационарности, введём в рассмотрение относительные значения времени: вместо и будем рассматривать относительные значения разностей аргументов во времени. Тогда получим, что корреляционная функция зависит от одного аргумента :

(4.46)

Мы получили функцию от одного аргумента , являющегося разностью двух моментов времени: . Эти аргумент и функция имеют основополагающее значение в теории случайных процессов. Для иллюстрации свойств корреляционной функции предположим, что . Тогда образуется формула вида:

(4.47)

Можно сделать и обратное определение: если математическое ожиданиеи дисперсия случайного процесса не зависят от времени, а корреляционная функция зависит от разности , то процесс считается стационарным в широком смысле. Само определение означает, что оно менее жесткое, и, следовательно, под него подходит большее количество случайных процессов.

Прежде чем объясняться в других определениях, рассмотрим свойства корреляционной функции типа (4.46). Заметим, что она определена на тот же случайный процесс . Предположим, что сдвиг во времени равен 0. Тогда выражение (4.46) примет вид:

(4.48)

Т. е. при минимальном сдвиге корреляционная функция равна дисперсии.

Предположим теперь, что при некотором значении значения функции независимы. Тогда, в соответствии с формулой Байеса:

(4.49)

где – двумерная условная плотность распределения. При условии независимости отсчетов она преобразуется в одномерную плотность распределения:

(4.50)

Тогда выражение (4.46) примет вид:

(4.51)

так как каждый из интервалов равен 0 как центральная моментная функция первого порядка.

Отсюда следует важный практический вывод: корреляционная функция оценивает взаимосвязь между значениями случайного процесса при временном сдвиге между отсчетами .

Определим свойства полученной функции:

1. . Это следует из определения, а также из предыдущих выкладок.

2. . Это вытекает их формул и окончательного вывода.

3. Корреляционная функция чётна:

(4.52)

Действительно, в общей формулировке стационарности можно принять . Тогда ; . Остальное очевидно.

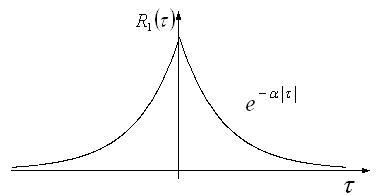
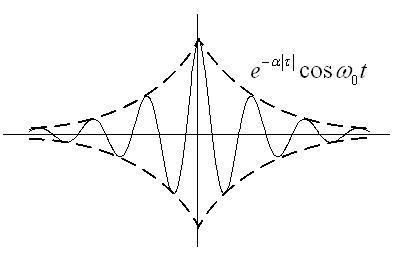
В связи с вытекающими свойствами, можно привести варианты нормированных корреляционных функций (см. рис. 4.20).

Рис. 4.20. Варианты реализаций корреляционных функций

Первый вариант случайного процесса – так называемая гладкая функция; сам процесс носит название пуассоновского. Вариант относится к классу узкополосных. Огибающая имеет ту же форму, что и в варианте , но несущая представляет собой гармоническое колебание постоянной частоты. Даже этими двумя примерами охватывается большой класс случайных процессов.

Первый тип описывает системы массового обслуживания с учетом независимого поступления заявок. В частности, этому закону распределения подчиняются интервал между следованиями транспорта на любой промежуточной остановке, очередь в парикмахерской или бане, вероятность поражения цели при ракетно-бомбовом ударе, вероятность столкновения во время спортивных соревнований.

Вариант имеет практическое приложение прежде всего в узкополосной речевой связи, когда существует несущая частота, относительно которой «вьётся» огибающая. Два типичных, и очень характерных примера – это речевая связь и описание системы электроснабжения. В первом случае объективно существует одна несущая частота и случайная огибающая, характеризующая собственно сообщение. Второй тип случайных процессов, системы электроснабжения, описывает следующую ситуацию. В единой системе электроснабжения имеется множество пользователей электроэнергии, подключающихся во времени случайно. При всяком случайном подключении происходят провалы напряжения (т. е. амплитуды несущей). Так как статистика подключений во времени потребителей и их мощности случайны, появляется зависимость относительно несущей частоты, описываемая функцией, изображенной на рисунке 4.20. Непонимание этого процесса приводит к тяжелым катастрофам, как это случилось в США в связи с массовыми отключениями энергосистем, в Московской области с теми же последствиями и в множестве других энергосистем (в частности, катастрофа на Саяно-Шушенской ГЭС)..

Можно привести множество аналогичных примеров, приведших к катастрофам, но достаточно большое их число связано с неграмотностью работников оборудования и ответственных за его эксплуатацию.

Очень важный раздел теории случайных процессов – эргодические случайные процессы. Это определение имеет очень важное прикладное значение, так как позволяет применить математический аппарат к реальным процессам.

Эргодическими называют такие случайные процессы, для которых усреднение по ансамблю реализации можно заменить усреднением по времени. Практически это означает, что можно исследовать один объект вместо однотипных объектов (что нереально). По одному объекту можно делать статистические обобщения на аналогичные технические объекты. Примеров можно привести достаточно много: баллистическая ракета, корабль, подводная лодка, самолет, электровоз, вагон, нефтеперегонная установка и т.д. Для исследования берут одни объект из серии однотипных и проводят на нем эксперименты.

С позиции теории вероятностей производятся следующие эквивалентные вычисления. Математическое ожидание заменяется средним по времени значением:

(4.53)

Здесь – интервал реализации, время, на котором происходит вычисление. В дискретной форме это выражение принимает вид:

(4.54)

Аналогичные выражения возможны и для других рассмотренных выше количественных оценок. В частности, для дисперсии интегральная и суммарная оценки принимают вид:

(4.55)

Аналогичные выражения существуют и для корреляционной функции:

(4.56)

Выражения (4.56) нуждаются в интерпретации. Появляется множитель , что приводит к неустойчивости вычислений при (любое случайное отклонение приводит к серьезным отклонениям от желаемого результата). Поэтому корреляционную функцию обычно вычисляют при . Проиллюстрируем сказанное графиком, приведенным на рис.4.21. Из графика видно, что корреляционная функция не затухает, что свидетельствует об отсутствии эргодичности. С позиции математики должны быть необходимое и достаточное свойства.

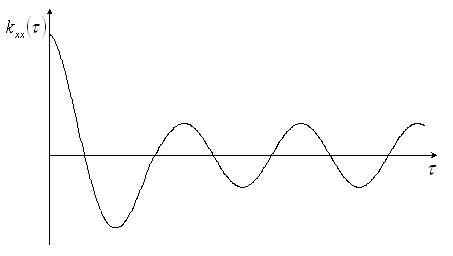
Рис. 4.21. Интерпретация задачи эргодичности

Необходимое условие: для того, чтобы процесс был эргодическим, необходимо, чтобы он был стационарным, т. е. должны выполняться условия:

(4.57)

Достаточное условие формулируется в следующей форме:

(4.58)

Это наиболее уязвимое свойство эргодичности, так как в соответствии с рисунком 4.21 абсолютное затухание корреляционной функции трудно доказать экспериментально. Более «мягкое» решение можно получить при следующем ограничении:

(4.59)

При экспериментальной обработке практических данных вступает в силу теория инженерных экспериментов. В основе теории лежит прикладная задача корректного описания конкретного объекта с целью оперативного наблюдения или управления. В качестве объектов наблюдения можно привести метеослужбу, службу мониторинга чрезвычайных ситуаций (землетрясения, извержения вулканов, торнадо, цунами, мощные пожары, катастрофы на транспорте). В перечисленных случаях важно корректное описание процессов. В частности, для технических систем выделяют три прикладных задачи анализа:

– генетика (апостериорный, т. е. послеопытный анализ): событие совершилось, нужно выявить его причины. В техническом приложении характерный пример – это рассмотрение причин произошедшей катастрофы. Существует система фиксирования текущего состояния объекта (чёрный ящик), которую после совершения инцидента «раскручивают» для поиска причин катастрофы.

– диагностика: оперативный контроль системы, включая выработку управляющих воздействий для восстановления рабочего состояния технической системы. Возможен второй вариант диагностирования, во время ремонта или периодического контроля, когда оценивается возможность дальнейшей эксплуатации или объем необходимого ремонта.

– прогностика: оценка возможности эксплуатации этого объекта с выработкой рекомендаций по времени ближайшей экспертизы.

Для решения упомянутых вопросов обязательно знание теории случайных процессов. В качестве приближений к желаемым результатам используются следующие приемы.

1. Уточнение интервала реализации с целью максимального приближения случайного процесса к свойствам стационарности и эргодичности. Как правило, в реальных случаях процессы не обладают свойствами стационарности. Варианты приближения к стационарности включают два приема:

– подгонка интервала реализации ;

– увеличение допуска на отклонение математического ожидания от выбранного значения.

В случаях «несрабатывания» этих приемов включаются два дополнительных механизма.

2. Обнаружение и устранение временного тренда. Тренд – это медленное изменение математического ожидания, проявляющееся в том, что на соседних интервалах отличается на величину, превышающую допуск. В качестве комментария на рис. 4.22 приведены реализации случайного процесса, отличающиеся средним значением , , . Для устранения нежелательных последствий эти средние значения вычитаются из последующих реализаций.

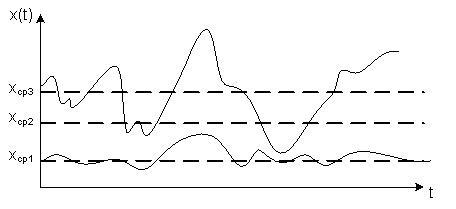
Рис. 4.22. К определению тренда

3. Обнаружение и устранение скрытой периодичности. Для этого достаточно обнаружить на графике корреляционной функции отсутствие затухания, как это показано на рисунке 4.23. Видно, что корреляционная функция не удовлетворяет требованию эргодичности, поэтому вводят составляющую , с помощью которой «гасят» эту периодическую составляющую.

Рис. 4.23. Обнаружение колебательности

Более тонкие механизмы обработки и интерпретации результатов статистических исследований приводятся в литературе [3, 10, 12].

Контрольные вопросы

1. В чем смысл формул Байеса для зависимых и независимых событий?

2. Как связаны между собой плотность и функция распределения вероятностей?

3. В чем смысл условия нормировки?

4. Чем определяются ограничения на амплитуду плотности распределения вероятности и на практический интервал?

5. Для чего вводят числовые оценки распределений?

6. Что характеризуют математическое ожидание и дисперсия?

7. В чем отличия определений стационарности в широком и узком смысле?

8. Дайте определение стационарности

9. Определите физический смысл и свойства корреляционной функции

10. Поясните физический смысл и свойства спектральной плотности мощности

11. Для чего вводится понятие эргодичности? Поясните необходимое и достаточные требования к эргодичности.