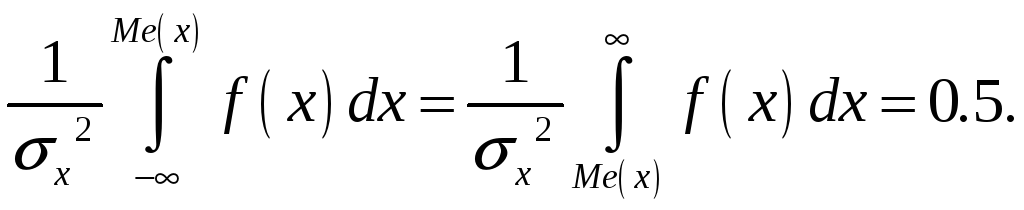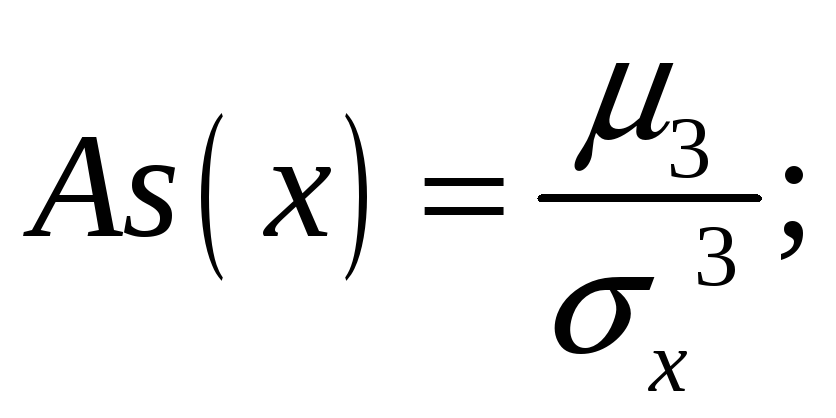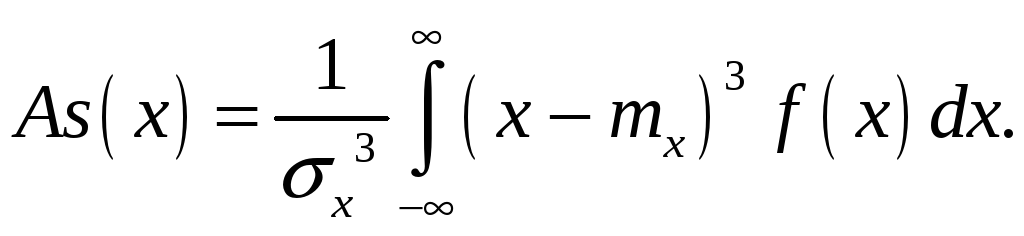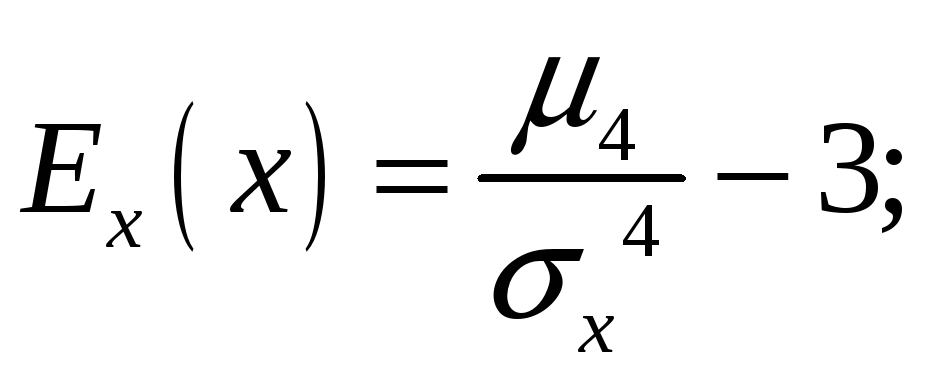- •В.Г. Шахов основы информационных технологий
- •Введение
- •Глава 1 Теоретические основы информационных технологий
- •1.1. Теория сигналов и спектральный анализ
- •1.2. Управление колебаниями
- •1.3. Теория информации
- •1.4. Дискретизация и квантование
- •Глава 2 Сжатие информации
- •2.1. Адаптивная дискретизация, разностная и дельта-модуляция.
- •2.2. Статистическое сжатие
- •2.3 Сжатие динамического диапазона.
- •2.4. Эффективное кодирование
- •2.5. Модификации кодов Хафмана
- •2.6. Алгоритмы Лемпеля – Зива
- •2.7. Сжатие графических изображений
- •2.8. Видеостандарт mpeg
- •Глава 3 Многоканальная передача и уплотнение линий связи
- •3.1. Сравнение и анализ основных методов разделения каналов
- •3.3. Адресное разделение каналов
- •3.4. Разделение каналов на основе псевдослучайных последовательностей
- •3.5. Комбинированное разделение каналов
- •Глава 4 Случайные процессы и их приложения
- •4.1. Основы теории случайных событий и величин
- •4.2 Основы теории случайных процессов
- •Глава 5 Основы цифровой обработки сигналов
- •5.1. Дискретные экспоненциальные функции (дэф)
- •5.2. Быстрое преобразование Фурье (бпф)
- •5.3. Применение теории чисел в цифровой обработке сигналов
- •5.5. Основы цифровой фильтрации
- •Глава 6 Борьба с помехами
- •6.1. Энергетические методы
- •6.2. Методы импульсной модуляции гармонической несущей
- •6.2. Простейшие методы приема импульсных сигналов
- •6.3. Помехоустойчивый прием модулированных колебаний при импульсной огибающей
- •6.3.1 Некогерентный ам-прием
- •6.3.2 Когерентный чм-прием
- •.3.3 Когерентный фм-прием.
- •6.4.Корректирующие коды.
- •6.4.1. Основные определения корректирующих кодов.
- •6.4.2. Алгебраические коды
- •6.4.3. Матричная запись линейных корректирующих кодов
- •6.4.4. Коды Рида - Маллера I рода
- •6.4.5. Полиномиальные коды
- •6.4.6. Итеративные коды
- •6.5. Непрерывные коды
- •6.5.1. Рекуррентные коды
- •6.5.2 Сверточное кодирование
- •6.5.3. Каскадные коды
- •6.5.4. Нелинейные коды
- •6.6. Системы с обратными связями
- •6.7. Комплексные решения помехоустойчивого приема.
- •Глава 7 Пример расчета параметров информационной системы
- •7.1. Основные сведения о системах телеизмерения
- •7.2. Содержание курсовой работы и исходные данные
- •7.3. Определение полосы занимаемых частот и построение спектральной диаграммы
- •7.3.1 Определение периода опроса
- •7.3.2. Определение верхней частоты спектра импульсной последовательности
- •7.3.3. Варианты модуляции
- •7.3.4. Выбор несущих и построение спектральной диаграммы
- •7.4. Определение максимального уровня помех в канале связи
- •7.4.1. Помехоустойчивость передачи импульсно-модулированных сигналов
- •7.4.2. Помехоустойчивость передачи кодовых посылок
- •7.5. Определение количества информации одного сообщения и скорости передачи информации.
- •7.6. Вычисление эффективности передачи
- •Заключение по курсовой работе
- •Общее заключение по учебному пособию
- •Библиографический список
- •Содержание
- •Глава 7 278
Глава 4 Случайные процессы и их приложения
4.1. Основы теории случайных событий и величин
В стандартном курсе высшей математики раздел теории вероятности излагается в трех частях: случайные события, случайные величины и случайные функции. Классическое изложение с математических позиций имеет серьезный изъян: оно не привязано к практике. Кроме того, в образовательном стандарте приводятся рекомендации в основном по первым двум разделам, хотя на практике важен третий, а именно случайные процессы.
Существует множество работ отечественных и зарубежных авторов, посвященных теории вероятности и ее приложениям. Наибольшую практическую значимость и адаптированность имеют работы Е.С. Вентцель, Г.Я. Мирского, Дж. Бендата, А. Пирсола, Б.Р. Левина, В.И Тихонова, Я.И. Хургина, А.М. Заездного.
В классической теории вероятности существует две основных гипотезы: однородности и независимости наблюдений.
Однородность предполагает независимость результатов опытов от времени их проведения. Классический пример – рулетка. Результат не зависит от времени суток, дня, недели, сезона и т.д.
Независимость означает, что каждый следующий опыт (эксперимент) не зависит от результатов предыдущих.
На практике гипотезы однородности и независимости должны подтверждаться экспериментально. В связи с этим в прикладной теории вероятностей существуют алгоритмы доказательств этих гипотез.
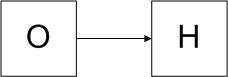
В дальнейшем изложении используем теорию кибернетики, согласно которой любое наблюдаемое явление (процесс) можно представить в виде «черного ящика»:
|
|
|
|
а) |
б) |
Рис. 4.1. Модели исследования объектов
где О – объект наблюдения (черный ящик), Н – наблюдатель. По первой модели (а), наблюдатель не имеет возможности воздействия на объект и просто накапливает статистику; по второй (б) – есть возможность активного влияния на объект.
С позиций теории вероятности, первые два раздела отличаются способом реализации или интерпретации объекта. В первом случае объект имеет два устойчивых состояния: 0 или 1. В таком варианте неважно, какой объект мы используем, важны лишь внешние описания. Второй вариант предполагает активное воздействие на объект с использованием обратной связи.
Теория
случайных величин предполагает, что
объект находится в одном из состояний,
0 или 1, причем пребывание объекта в этих
состояниях случайно. Время в данном
случае не входит в число аргументов.
Как правило, в математике используют
обе вышесказанные теории и принимают
следующие определения. Допустим,
произведено
![]() независимых опытов, удовлетворяющих
обеим гипотезам. При этом количество
опытов, приводящих объект в состояние
0, равно
независимых опытов, удовлетворяющих
обеим гипотезам. При этом количество
опытов, приводящих объект в состояние
0, равно
![]() ,
в состояние 1 –
,
в состояние 1 –
![]() .
тогда вероятность
.
тогда вероятность
![]() выходного состояния
выходного состояния
![]() определяется соотношением:
определяется соотношением:
|
|
(4.1) |
Аналогично противоположное состояние
|
|
(4.2) |
Удачно предложенные концепции предполагают соотношения:
|
|
(4.3) |
Приведенные соотношения (4.2) (4.3) позволяют судить о взаимосвязанных событиях.
В
теории случайных событий часто
используются графические аналогии в
виде диаграмм Эйлера-Венна [33]. При этом
полная (генеральная) сетка событий
первого типа оценивается формулой (4.1)
и его альтернативой типа (4.2). Общая
совокупность из
![]() опытов представляется в виде прямоугольника
опытов представляется в виде прямоугольника
![]() (полная группа событий), вероятности
(полная группа событий), вероятности
![]() и
и
![]() – в виде кругов Эйлера-Венна (рис. 4.2).
– в виде кругов Эйлера-Венна (рис. 4.2).
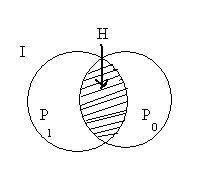
Рис. 4.2. Вероятностная интерпретация событий
Здесь
![]() – полное множество возможных исходов,
– полное множество возможных исходов,
![]() – исходы типа 1,
– исходы типа 1,
![]() – исходы типа 0. Существует зона
неопределенности
– исходы типа 0. Существует зона
неопределенности
![]() ,
в которой нельзя принять решений.
,
в которой нельзя принять решений.
В соответствии с формулами (4.2) и (4.3) и кругами Эйлера-Венна справедливы следующие математические соотношения:
|
|
(4.4) |
|
|
(4.5) |
Последнее выражение имеет название формулы Байеса [7] для независимых событий. В случае зависимых событий в алгебраической форме выражение (4.5) приобретает вид:
|
|
(4.6) |
Здесь
![]() и
и
![]() образуют совокупность двух событий,
причем
образуют совокупность двух событий,
причем
![]() является вероятностью события
является вероятностью события
![]() ,
,
![]() – вероятность совместного события, а
– вероятность совместного события, а
![]() – условная вероятность того, что событие
– условная вероятность того, что событие
![]() состоялось.
состоялось.
Выражения (4.5) и (4.6) являются краеугольными в области теории вероятности.
Перейдем теперь к теории случайных величин. Можно обратиться к моделям на рис. 4.1 при условии, что выходная величина непрерывна. Например, мы изучаем скорость движения поезда. На нее влияет множество ограничений: тип поезда, состояние пути, временные ограничения по скорости, метеоусловия, соседние поезда и т.д. Общая совокупность ограничений образует достаточно сложную картину, в ходе которой результирующая скорость приобретает характер случайной величины. Основная функция, описывающая поведение случайной величины, – плотность распределения вероятности.
Для
исследования любой случайной величины
![]() необходима последовательность действий,
представленная на рис. 4.3.
необходима последовательность действий,
представленная на рис. 4.3.

Рис. 4.3. Исследование непрерывного объекта
Здесь
АЦП – аналого-цифровой преобразователь,
Рег – регистратор событий. Не усложняя
процедуры, будем считать, что
последовательность считывания значений
![]() равномерна с шагом
равномерна с шагом
![]() .
Тогда за время
.
Тогда за время
![]() (время реализации) мы получим
(время реализации) мы получим
![]() отсчетов, причем
отсчетов, причем
![]() .
Разобьем интервал возможных значений
на
.
Разобьем интервал возможных значений
на
![]() подынтервалов. В этом случае можно
фиксировать количество попаданий в
подынтервалов. В этом случае можно
фиксировать количество попаданий в
![]() -й
интервал как
-й
интервал как
![]() или в относительной форме как
или в относительной форме как
![]() .
Полученная зависимость называется
гистограммой распределения вероятности
и графически представляется в следующей
форме:
.
Полученная зависимость называется
гистограммой распределения вероятности
и графически представляется в следующей
форме:
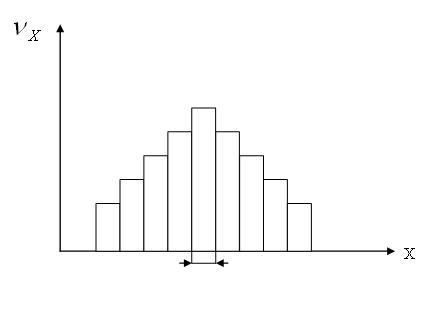
Рис. 4.4. Гистограмма распределения
Здесь
![]() -
ширина подынтервала,
-
ширина подынтервала,
![]() -
относительная частота попадания в него:
-
относительная частота попадания в него:
|
|
(4.7) |
Предположим,
значение
![]() неограниченно уменьшается, а количество
подинтервалов при этом возрастает. При
этом получается оценка, сформулированная
Л. Эйлером [7] и приобретающая свойства
гладкой функции
неограниченно уменьшается, а количество
подинтервалов при этом возрастает. При
этом получается оценка, сформулированная
Л. Эйлером [7] и приобретающая свойства
гладкой функции
![]() .
Функция впоследствии получила название
плотности распределения вероятности.
Это фундаментальное определение, на
котором держится базовая теория. Приведем
основные свойства плотности распределения.
.
Функция впоследствии получила название
плотности распределения вероятности.
Это фундаментальное определение, на
котором держится базовая теория. Приведем
основные свойства плотности распределения.
1. Условие нормировки. Исходя из соотношения (1.8), очевидно, что:
|
|
(4.8) |
откуда следует, что сумма наблюдений равна генеральной совокупности. Следовательно, справедлива формула:
|
|
(4.9) |
или в интегральной форме
|
|
(4.10) |
Условие нормировки является фундаментальным и наиболее очевидным в теории вероятности. Действительно, вероятность принятия случайной величиной любого из возможных значений достоверна, т. е. равна 1, что и выражается формулами (4.9) и (4.10).
2.
Положительная определенность. На
любом интервале
![]() функция
функция
![]() неотрицательна. Это вытекает из первого
свойства. Так как вероятность не может
быть отрицательной по определению, а
она оценивается интегралом от плотности
распределения:
неотрицательна. Это вытекает из первого
свойства. Так как вероятность не может
быть отрицательной по определению, а
она оценивается интегралом от плотности
распределения:
|
|
(4.11) |
то
на любом интервале
![]() должен быть положительный результат.
должен быть положительный результат.
В результате перехода к непрерывной величине получаем гладкую кривую, представленную на рисунке 4.5
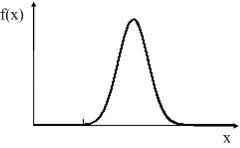
Рис. 4.5. Плотность распределения вероятностей
На практике существует конечное множество типичных распределений случайных величин. Наиболее полный их перечень приведен в книге А.Н. Заездного [12].
Среди всех возможных распределений наиболее значимо нормальное распределение, описываемое выражением:
|
|
(4.12) |
Здесь
![]() и
и
![]() – математическое ожидание и дисперсия
случайной величины, определения которых
будут даны позже.
– математическое ожидание и дисперсия
случайной величины, определения которых
будут даны позже.
Нормальное распределение является базовым вследствие центральной предельной теоремы Ляпунова [17]. Согласно теореме, если в результирующей случайной величине участвуют четыре о более независимых составляющих, то результирующее распределение нормально.
Второе
распределение, используемое на практике,
– равномерное. Для него существует
следующее определение. Предположим, на
интервале
![]() функция существует, а вне этих значений
равна нулю. Учитывая условие нормировки,
получаем:
функция существует, а вне этих значений
равна нулю. Учитывая условие нормировки,
получаем:
|
|
(4.13) |
|
|
|
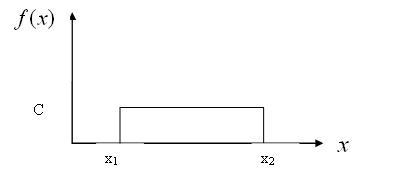
Рис. 4.6. Равномерное распределение
Равномерное распределение считается наиболее жестким для практических приложений, так как здесь абсолютно не сглаживаются исходы случайных выборок. Такая жесткая модель используется, например, в теории систем массового обслуживания (СМО). При моделировании таких систем наиболее важны критические ситуации, а хуже, чем равновероятные события, в этом смысле нет.
Исследование случайных величин производится в следующей последовательности:
1.
Накапливаются статистические данные
методов наблюдения за объектом и
получение отсчетов с интервалом
![]() .
При этом по умолчанию предполагается,
что соседние отсчеты независимы.
.
При этом по умолчанию предполагается,
что соседние отсчеты независимы.
2. Строится гистограмма распределения
3.
Проводится аппроксимация гистограммы
к одному из канонических распределений
на основе критериев согласия. Один из
таких критериев,
![]() –
критерий согласия Пирсона относится к
нормальному распределению и является
наиболее употребляемым. Его легко можно
обобщить на любое типовое распределение
по следующему алгоритму:
–
критерий согласия Пирсона относится к
нормальному распределению и является
наиболее употребляемым. Его легко можно
обобщить на любое типовое распределение
по следующему алгоритму:
4.
Накапливается совокупность из N
дискретных и желательно независимых
отсчетов
![]() .
.
5.
Выбирается аппроксимируемая функция
![]() ,
к которой может приближаться полученная
гистограмма распределения.
,
к которой может приближаться полученная
гистограмма распределения.
6. Производится оценка качества аппроксимации методом суммирования разностей гладкой функции и совокупности отсчетов:
|
|
(4.14) |
7. Выбирается критерий согласия в виде константы М, относительно которой справедливы следующие утверждения:
–
если
![]() ,гипотеза
является состоятельной;
,гипотеза
является состоятельной;
–
если
![]() ,
гипотеза отвергается.
,
гипотеза отвергается.
Это
сценарий «жестких решений». В настоящее
время большой популярностью пользуется
метод мягких решений, или метод нечетких
множеств. Согласно методу вводится
интервал неопределенности
![]() ,
в соответствии с которым алгоритмы
оценивания приводятся к виду:
,
в соответствии с которым алгоритмы
оценивания приводятся к виду:
–
если
![]() ,
гипотеза состоятельна;
,
гипотеза состоятельна;
–
если
![]() ,
гипотеза отвергается;
,
гипотеза отвергается;
–
если
![]() ,
гипотеза не определена, и необходимо
дополнительное исследование.
,
гипотеза не определена, и необходимо
дополнительное исследование.
Проиллюстрируем сказанное графическими изображениями. На рис. 4.7 представлены гистограмма распределения случайной величины и аппроксимирующая функция. Применяя формулу (4.14), мы можем использовать критерий жестких решений или нечетких множеств. Последнее относится к теории обучающихся систем и имеет более высокую производительность. Такие системы и алгоритм являются основой так называемых интеллектуальных систем (искусственный интеллект, ИИ).
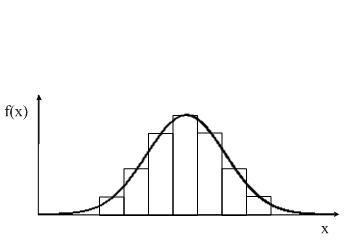
Рис. 4.7. Оценка качества аппроксимации
Возможны
более сложные многомерные распределения,
когда случайная величина зависит от
двух и более аргументов. В этом случае
рассматриваются функции
![]() ,
,
![]() и
т.д. В частности, двумерная плотность
распределения представляет поверхность,
как показано на рис. 4.8. По этой поверхности
можно проводить сечения по трем
координатам,
и
т.д. В частности, двумерная плотность
распределения представляет поверхность,
как показано на рис. 4.8. По этой поверхности
можно проводить сечения по трем
координатам,
![]() и
и
![]() .
В первых двух случаях в сечении получается
одномерная плотность распределения
при фиксированной второй координате,
т. е.
.
В первых двух случаях в сечении получается
одномерная плотность распределения
при фиксированной второй координате,
т. е.
![]() или
или
![]() – условные плотности распределения. В
третьем случае образуется двумерная
фигура, т. е. некоторый эллипс распределения.
– условные плотности распределения. В
третьем случае образуется двумерная
фигура, т. е. некоторый эллипс распределения.
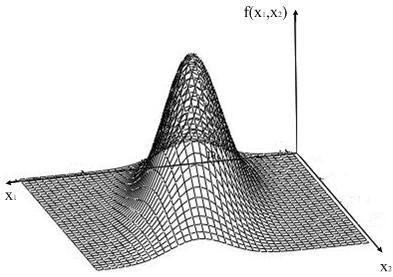
Рис. 4.8. Двумерная плотность распределения
На практике описание ситуации пытаются упростить. Один из вариантов упрощения – сведение многомерных функций распределения к функциям меньшего порядка. Простейший вариант упрощения – те же формулы Байеса. Для рассмотренного нами варианта функции двух случайных аргументов можно записать:
|
|
(4.15) |
Это и есть распространение формулы Байеса на случайные величины.
Даже
в случаях одномерных распределений,
близких к типичным, появляются
дополнительные проблемы, в том числе
вычислительные. В таких случаях переходят
к числовым характеристикам случайных
величин. Они образуют два семейства:
начальные и центральные моменты.
Начальный момент порядка
![]() определяется
из выражения:
определяется
из выражения:
|
|
(4.16) |
|
|
|
или в дискретной форме:
|
|
(4.17) |
Центральный
момент
![]() -го
порядка определяется из соотношения:
-го
порядка определяется из соотношения:
|
|
(4.18) |
или в дискретной форме:
|
|
(4.19) |
Наиболее значимы начальный момент первого порядка, называемый математическим ожиданием, и центральный момент второго порядка – дисперсия. Математическое ожидание эквивалентно среднему значению случайной величины, а дисперсия – разбросу относительно математического ожидания. Математическое ожидание имеет вид:
|
|
(4.20) |
Соответственно выражения для дисперсии запишутся в виде:
|
|
(4.21) |
Приведенные
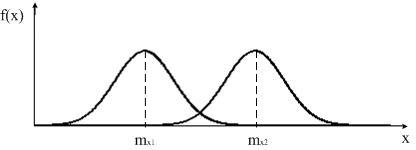
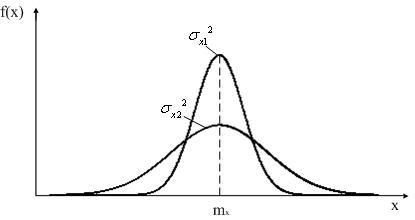
соотношения проиллюстрируем графически.
На рис. 4.9 приведены плотности распределения
вероятностей для двух различных
вариантов. Вариант
![]() соответствует
различным математическим ожиданиям,
соответствует
различным математическим ожиданиям,
![]() –
различным дисперсиям.
–
различным дисперсиям.
|
|
|
|
а) |
б) |
Рис. 4.9. Варианты распределений
Из
рисунка видно, что
![]() ,
а
,
а
![]() .
.
Как правило, этих числовых оценок достаточно для множества практических приложений. Иногда для частных задач используются другие числовые оценки. Назовем наиболее употребимые.
Мода – значение случайной величины, при которой плотность распределения имеет максимум:
|
|
(4.22) |
На рис. 4.10 приведён пример плотности распределения. Здесь же приведено значение математического ожидания, из чего следует, что при несимметричных распределениях мода и математическое ожидание не совпадают.
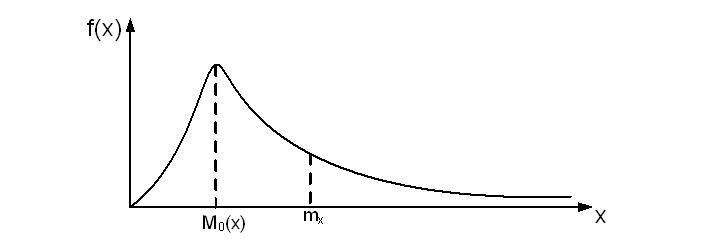
Рис. 4.10. К определению моды
Возможны распределения с несколькими максимумами. Они называются полимодальными. Пример полимодального распределения приведён на рис. 4.11.
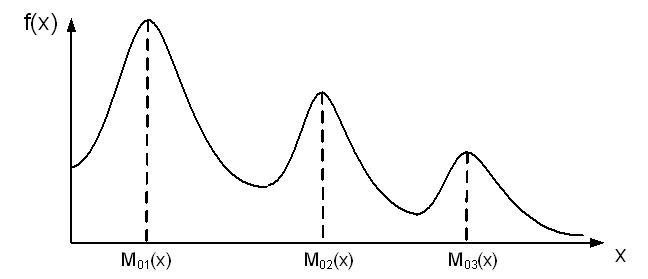
Рис. 4.11. Полимодальное распределение
Кроме этого существуют так называемые антимодальные распределения.
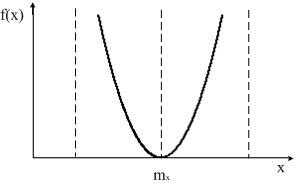
Рис. 4. 12. Антимодальное распределение
В качестве примера приведем задачу о случайном выборе точки на гармоническом сигнале (см. рис. 4.13). Без приведения математических выкладок запишем окончательный результат. Плотность распределения вероятности такой случайной величины равна:
|
|
(4.23) |
|
|
|
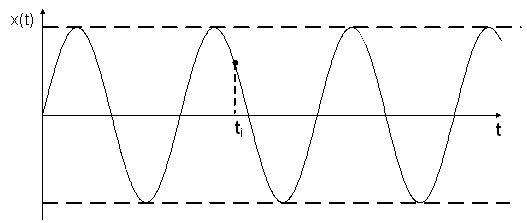
Рис. 4.13. Случайные выборки на гармоническом сигнале
Такое распределение имеет название закона арксинуса и плотность распределения для него:
|
|
(4.24) |
|
|
|
Другая количественная оценка – медиана. Это такое значение случайной величины, при котором её вероятности слева и справа от нее равновероятны:
|
|
(4.25) |
В интегральной форме соотношение (4.25) принимает вид:
|
|
(4.26) |
Если распределение симметрично, то медиана совпадает с математическим ожиданием, что иллюстрируется рис.4.14. Заштрихованные области равны по площади, составляющей 0,5.
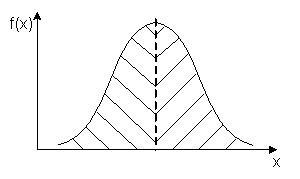
Рис. 4.14. К определению медианы
Центральный момент третьего порядка называется асимметрией. Он характеризует отклонение распределения от нормального. Выражение для асимметрии имеет вид:
|
|
(4.27) |
На рис. 4.15 показаны два типа асимметричных распределений. Левое, со знаком «+», соответствует положительной асимметрии, правое – отрицательной.
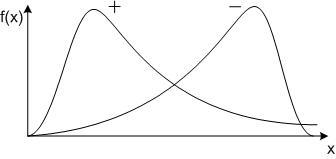
Рис. 4.15. К определению асимметрии
Еще одна количественная оценка – эксцесс. Это степень отличия распределения от нормального. В нормированном виде он представляет собой центрированный момент четвертого порядка:
|
|
(4.28) |
«Довесок» – 3 в формуле (4.27) означает, что центральный момент четвертого порядка для нормального распределения равен 3.
Другие моментные характеристики обычно не используются.
Второй
вид функций, описывающих распределения
случайных величин, – функции распределения
![]() .
Функция распределения от аргумента
.
Функция распределения от аргумента
![]() – это вероятность случайной величины
попасть в полубесконечный интервал
– это вероятность случайной величины
попасть в полубесконечный интервал
![]() :
:
|
|
(4.29) |
В связи с такой трактовкой можно описать свойства функции распределения.
1.
Положительная определенность. Для
любых значений
![]()
![]() неотрицательна:
неотрицательна:
|
|
(4.30) |
Положение
(4.30) доказывается методом от противного.
Предположим, что на некотором интервале
![]() значения
значения
![]() отрицательны. Тогда в соответствии с
(4.30) появляется возможность отрицательной
вероятности, что противоречит определению.
отрицательны. Тогда в соответствии с
(4.30) появляется возможность отрицательной
вероятности, что противоречит определению.
2. Ограниченность. В соответствии с определением вероятность не может превосходить 1. Поэтому справедливы следующие ограничения:
|
|
(4.31) |
3.
Интервальность. Вероятность попадания
случайной величины в интервал
![]() определяется в виде разности функций
распределения:
определяется в виде разности функций
распределения:
|
|
(4.32) |
В
связи со свойствами
![]() существуют взаимно однозначные
соотношения:
существуют взаимно однозначные
соотношения:
|
|
(4.33) |
На
практике предпочитают плотность
распределения вместо функции распределения.
Это определяется лучшей визуальной
информативностью функции
![]() ,
т.к. основные свойства видны сразу: мода,
математическое ожидание, асимметрия и
дисперсия «прощупываются» на основе
графического образа распределения.
Также на практике достаточно беглого
оперативного сравнения различных
случайных величин.
,
т.к. основные свойства видны сразу: мода,
математическое ожидание, асимметрия и
дисперсия «прощупываются» на основе
графического образа распределения.
Также на практике достаточно беглого
оперативного сравнения различных
случайных величин.


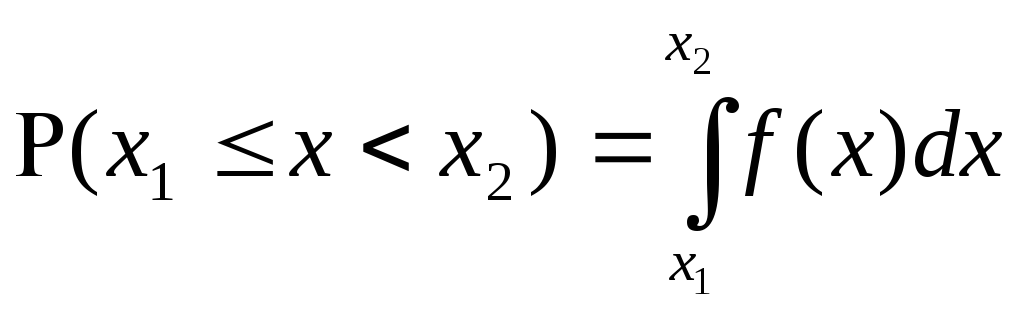 ,
,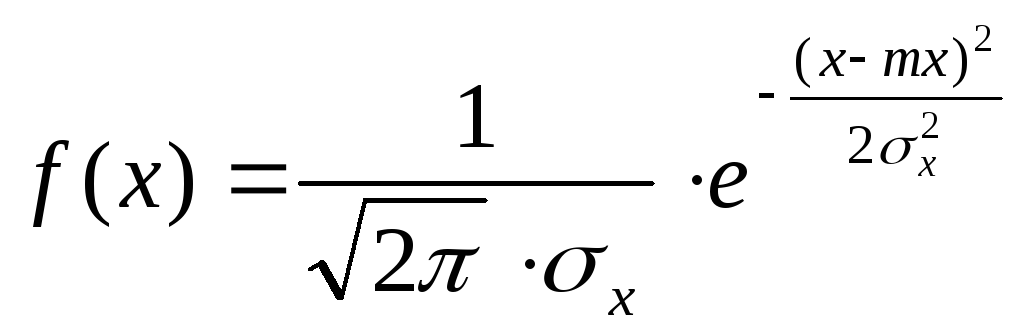 ,
,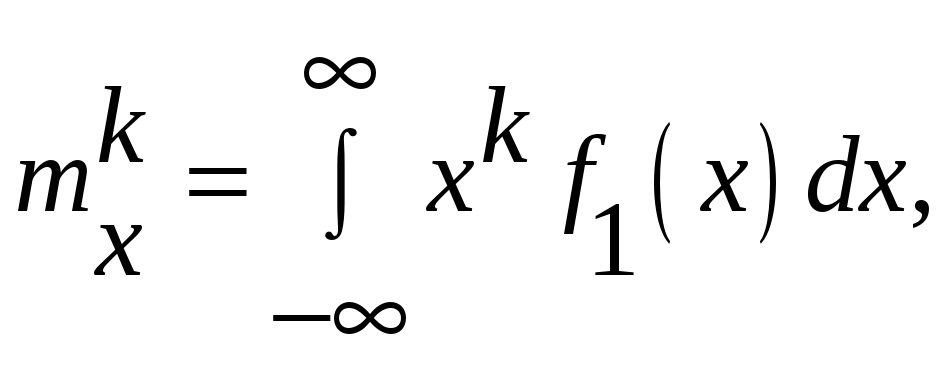
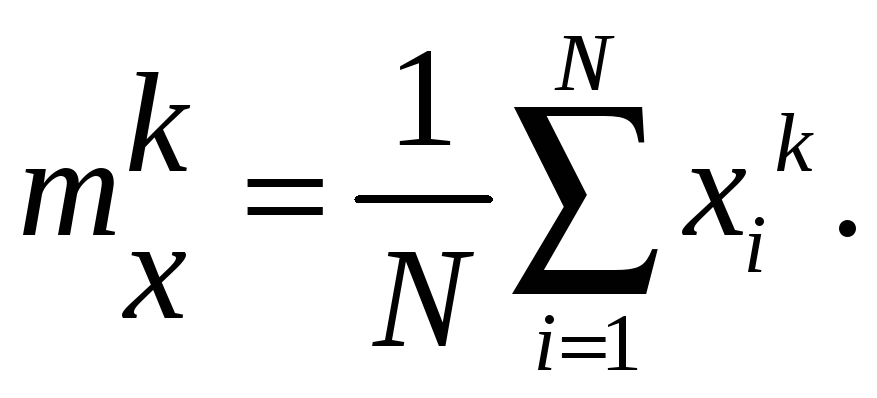
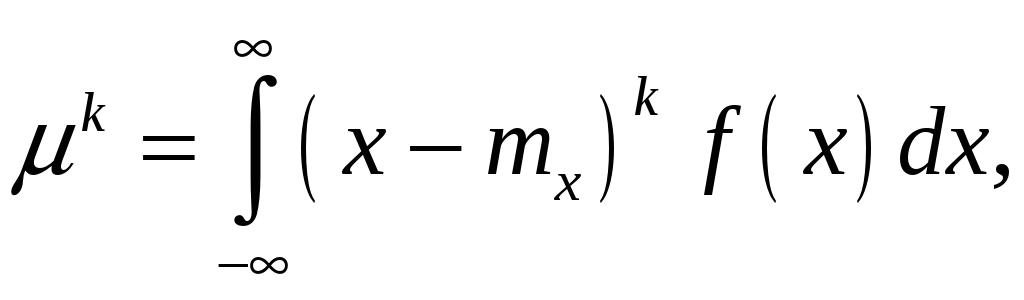
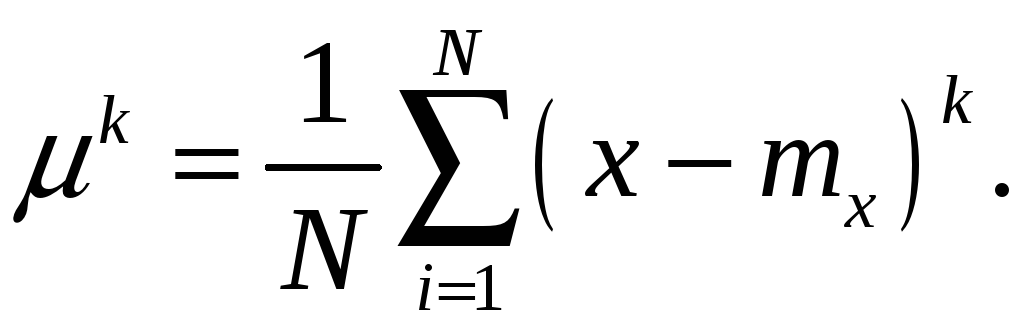
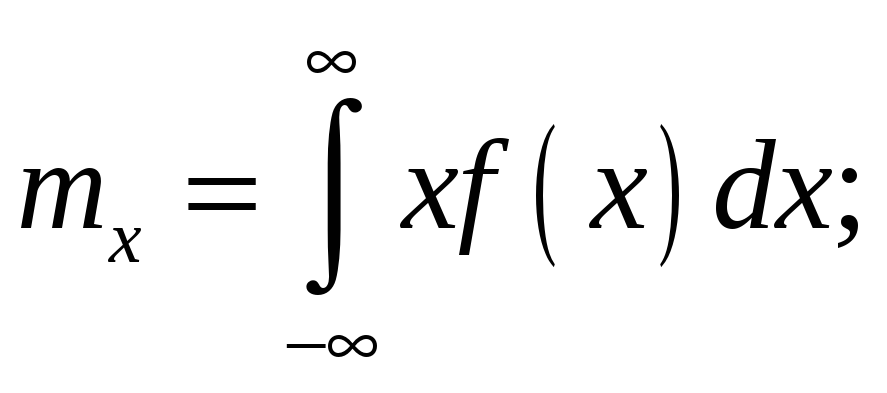
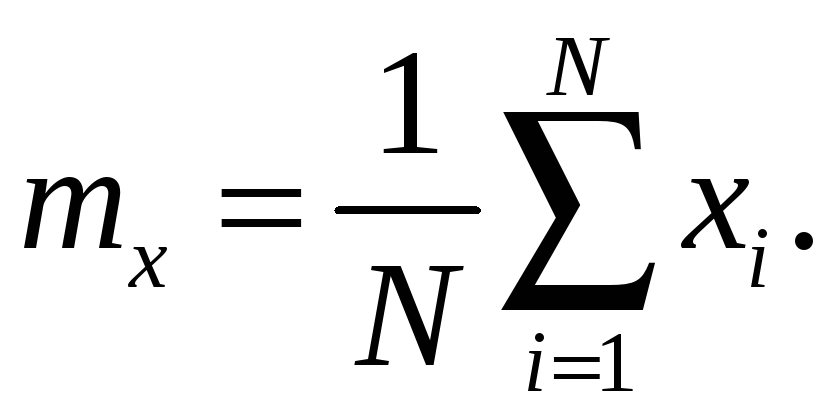
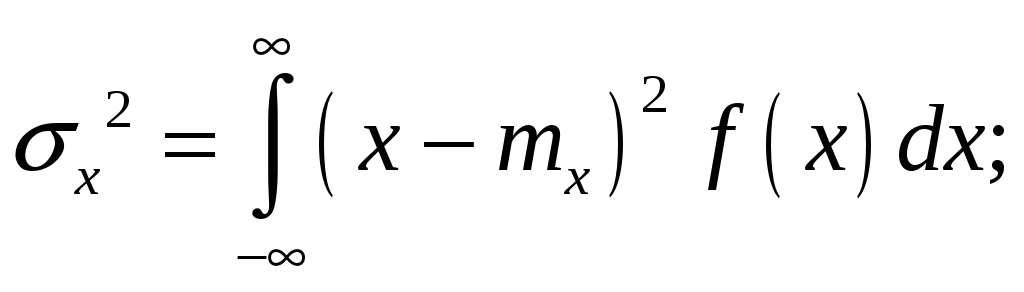
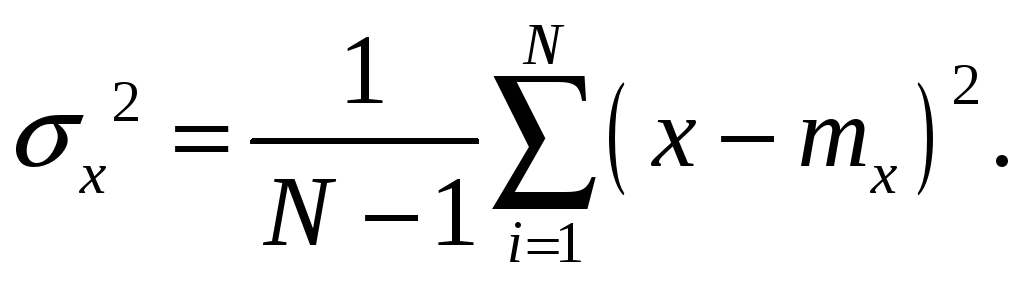
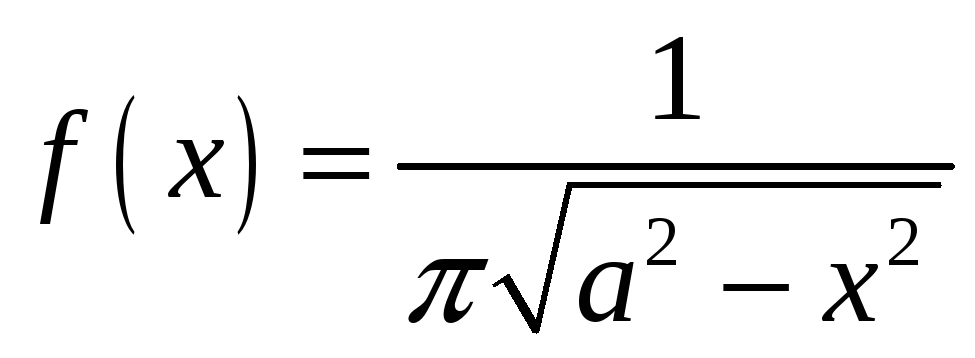 .
.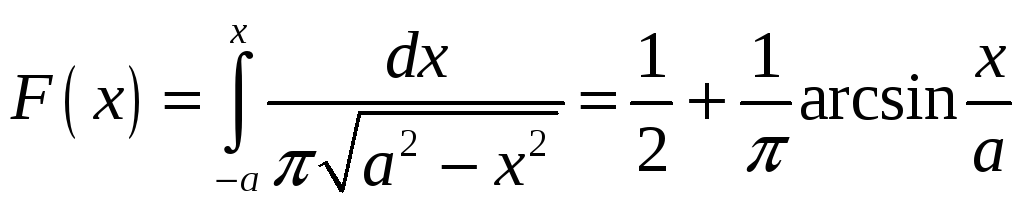 .
.