3.3. Адресное разделение каналов
Адресное
разделение относится к асинхронным и
является достаточно эффективным по
сравнению с временным или частотным.
При числе каналов (адресатов)
эффективность ее достигает величины
.
Сущность адресного разделения достаточно
проста: перед информационным пакетом
в передаваемое сообщение добавляется
код адресата (он еще называется адресом
приемника), указывающий, кому предназначено
сообщение. Количество различных адресов
(другими словами, число различных кодовых
комбинаций)
,
где
– число двоичных разрядов, откуда и
вытекает выражение для эффективности.
При большом числе абонентов и дуплексной (то есть двусторонней) связи к адресу приемника добавляется и адрес источника, что позволяет легко идентифицировать абонентов.
3.4. Разделение каналов на основе псевдослучайных последовательностей
Этот метод применяется для некоторых типов спутниковых сетей связи [40]. Сущность его сводится к тому, что проводится логическая операция поразрядное сложение по модулю 2, в которой один операнд – передаваемая информация, а второй – псевдослучайная последовательность (ПСП).
Псевдослучайной
называется последовательность цифр
(чаще нулей и единиц), в которой
закономерность выявить трудно, но через
какое-то число символов она повторяется.
Число символов
,
через которое повторяется ПСП, называется
периодом повторения. Очевидно, что, чем
больше
,
тем генератор ПСП лучше. Рассмотрим
свойства ПСП.
1. Если ПСП участвует в линейной операции, ее результат обладает свойством обратимости. Это значит, что если результат подвергнуть обратной линейной процедуре, первый сооперанд восстанавливается.
2.
ПСП обладают свойством ортогональности.
Если обозначить ПСП в виде функции
,
где
– номер такта, то ортогональность
запишется в виде
|
|
(3.5) |
.
Здесь
– логическая
операция «сложение по модулю 2» или
«исключающее ИЛИ». Эта операция характерна
своей обратимостью, то есть в логическом
выражении (уравнении), основанном на
ней, можно переносить члены из левой
части в правую и наоборот без изменения
знака. Условие ортогональности (3.5) можно
расширить на любую другую ПСП
того же (или другого) периода повторения:
|
|
(3.6) |
.
Для
пояснения смысла этих свойств обратимся
к чертежу системы разделения каналов
на базе ПСП (рис.3.5). Здесь знаком
оказана та же процедура «сложение по
модулю 2». Если генераторы ПСП одинаковы
и работают синхронно, процедура связи
обратима в силу ортогональности (3.5).
Если же генераторы разные или работают
со сдвигом, процедура связи необратима,
то есть в приемнике передаваемые символы
не восстанавливаются, а образуется
случайный набор символов. В выражении
(3.5)
– вес ПСП, то есть количество содержащихся
в ней единиц (обычно
близко к
).
Рис. 3.5. Разделение каналов на основе ПСП
Такой способ разделения каналов обеспечивает, кроме того, секретность передачи, но имеет очень низкую частотную эффективность (порядка 2%), поэтому может использоваться только в широкополосных линиях связи (радиолинии СВЧ-диапазона, волоконно-оптические).
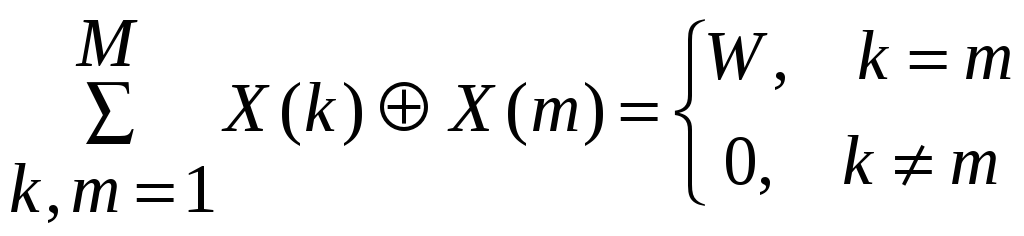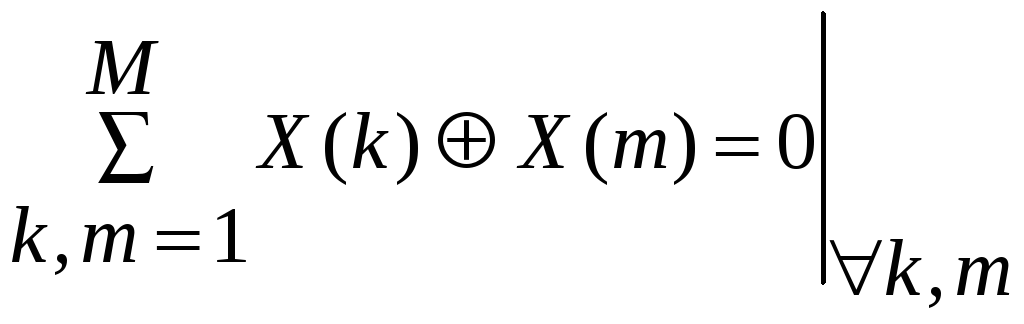