2.3. Математические модели входных воздействий.
x
0
t
Рис.
2.3. График
ступенчатой
функции
С
тупенчатая
функция (единичный скачок).В
момент t
= 0 воздействие
мгновенно
достигает
величины x
= 1, далее со временем не меняется. График
показан на рис. 2.3.
Единичную ступенчатую функцию записывают символом 1(t).
t 0 1(t) = 0,
t = 0 1(t) = 1,
t 0 1(t) = 1.
Если воздействие ступенчатое, но отличается от единичного в А раз, его обозначают А(1). А(1) = А1(t).
Импульсная
функция (единичный импульс).
Это такой импульс величина которого
равна бесконечности, длительность -
нулю, а площадь – единице. В математике
известен как дельта функция. Обозначается
.
t 0 (t) = 0,
t = 0 (t) = ,
t 0 (t) = 0.
Единичный импульс есть производная от единичной ступенчатой функции:
Импульсную функцию можно трактовать как предел прямоугольного импульса, у которого высота стремится к , а время его действия – к нулю.
Гармоническая функция. Это функция, изменяющаяся по закону синуса или косинуса.
Записывается либо
как
либо
как
.
Величина воздействия колеблется между значениями A и -A.
Линейная функция.
.
Воздействие возрастает пропорционально времени.
Квадратичная функция.
.
Воздействие возрастает пропорционально квадрату времени.
2.4. Переходная функция.
С момента воздействия x(t) на вход системы, управляемая величинаy(t) начинает изменяться. Процесс, происходящий в это время, называют переходным. Аналитическая зависимостьy(t), описывающая переходной процесс, называетсяпереходной функцией. Будет система управляться лучше или хуже – зависит от переходной функции.
Переходной процесс обуславливается внутренними свойствами системы и видом воздействия. Чтобы иметь возможность сравнивать переходные процессы разных систем, принято оказывать воздействие в виде единичной ступенчатой функции при нулевых начальных условиях. Переходную функцию обозначают h(t).
Первую производную от переходной функции называют весовой функциейи обозначаютw(t).
Переходные функции подразделяются на три вида в зависимости от того, как ведет себя производная w(t) =dh/dt.
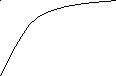
1. Монотонные. Первая производная не меняет знак:dh/dt либо0, либо0. Пример на рис. 2.4.
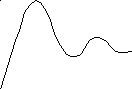
2. Колебательные. dh/dt регулярно меняет плюс на минус и наоборот. Пример на рис. 2.5.
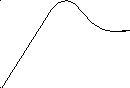
3. Апериодические.dh/dt меняет знак один раз. Пример на рис. 2.6.
h
(t)
1
2
0 t
Рис. 2.4. Монотонно меняющиеся кривые
h (t)
t
Рис. 2.5. Затухающие колебания
h
(t)
1
2
0
t
Рис. 2.6. Апериодические кривые
Все функции могут быть получены как решение одного дифференциального уравнения при разном значении его коэффициентов или, что все равно, при разном значении коэффициентов характеристического уравнения. Решение характеристического уравнения общего вида (2.7) дает n корней (комплексных, действительных, мнимых). Общее решение линейного однородного дифференциального уравнения есть сумма n экспонент,
,
где ci – постоянные интегрирования, pi – корни характеристического уравнения. Действительные корни, p = , обеспечивают неограниченный рост или уменьшение до нуля соответствующих экспонент. Комплексные корни, p = j , обеспечивают возрастающие или затухающие колебания. Экспоненты с чисто мнимыми корнями, p = j , обеспечивают гармонические колебания (колебания с постоянной амплитудой).
В зависимости от коэффициентов, наличие, количество тех или иных видов корней будет меняться, что и обеспечивает тот или иной вид кривых переходного процесса.
Аналитическое выражение кривой переходного процесса можно получить двумя путями. Первый – непосредственное решение дифференциального уравнения, описывающего систему. Надо положить величину входного воздействия x = 1 и выполнить нулевые начальные условия. Второй – на основе операторного уравнения. Надо ввести в него изображение единичного ступенчатого воздействия и выполнить обратное преобразование Лапласа.
В некоторых системах автоматического управления важную роль играют импульсные переходные функции. Их получают, подавая на вход системы единичный импульс. Импульсная переходная функция отличается от «ступенчатой», поскольку как было сказано выше, импульсная функция есть производная от ступенчатой:
.
Пример 2.5.
Процесс
в объекте описывается дифференциальным
уравнением
Найти переходную функцию.
Вводим условие единичного ступенчатого воздействия, полагая x = 1. Ищем решение дифференциального уравнения при нулевых начальных условиях. Решением будет переходная функция h(t), поэтому сразу можно y(t) заменить на h(t).
Общее решение неоднородного уравнения
есть сумма решений h1 + h2. Первое получают, решая однородное уравнение
.
Решением
будет
Второе решениеh2
есть частное
решение неоднородного уравнения, которое
можно выбрать как h2
= k.
Общим решением будет:
C учетом того, что h = 0 при t = 0, окончательное выражение для переходной функции получается в виде:
.
П
Найти переходную функцию для системы, описываемой дифференциальным уравнением
Запишем операторное уравнение
(5p + 1) Y(p) = (3p + 2) X(p)
в виде
Множитель при X(p) есть не что иное, как передаточная функция. X(p) – изображение произвольного воздействия. Воздействие в виде единичного ступенчатого скачка имеет изображение X(p) = 1/p. Если в операторном уравнении заменить X(p) на 1/p , то на Y(p) накладывается требование быть изображением переходной функции. Подчеркивая это, заменим Y(p) на H(p). Получаем операторное уравнение для переходной функции:
.
Прежде чем воспользоваться таблицей изображений по Лапласу, представим правую часть уравнения в виде суммы:
.
В таблице находим оригиналы по их изображениям:
,
,
.
В нашем случае T = 5. Множители 3 и 2 сохраняют свое значение и место. Окончательно
,
или
h(t) = 2 – 1,4e t / 5 .