Находим передаточную функцию замкнутой системы

.

Записываем характеристический полином замкнутой системы

D(p) = p³ + 2 p² + 3 p + 4

и соответствующий ему комплексный частотный полином

D(j) = - j³ - 2 ² + j3 + 4 .

Его действительная и мнимая части:

U() = 4 - 2² , V() = 3 - ³ .

Определяем частоты пересечения, координаты точек пересечения, углы.

V() = 0. ₁ = 0, U() = 4, () = 0.

₃ = ,U() = -2, () = 2 (/2).

U() = 0. ₂ = , V() = , () = (/2).

 =  () = -3(/2).

Требование ₁ < ₂ < ₃ выполняется, углы последовательно возрастают, вектор D(j) делает поворот на 3(/2) радиан.

Вывод: система устойчивая.

5.4. Критерий Найквиста

Устойчивость замкнутой системы определяется по годографу комплексной частотной характеристики разомкнутой системы.

Обратимся к передаточной функции разомкнутой системы,

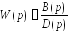. (2.6)

Характеристический полином есть D(p) . Устойчивость разомкнутой системы определяется по характеристическому полиному D(p) .

Иными словами он содержит в себе информацию об устойчивости разомкнутой системы.

Если система замкнутая, ее передаточная функция

. (5.4)

Характеристический полином есть D(p) +B(p) . Устойчивость замкнутой системы определяется по характеристическому полиномуD(p) +B(p) . То есть, в нем содержится информация об устойчивости замкнутой системы. Отношение передаточных функций (2.6) и (5.4) есть отношение характеристического полинома замкнутой системы к характеристическому полиному разомкнутой системы:

.

Значит, содержит в себе информацию об устойчивости как замкнутой, так и разомкнутой системы. Устойчивость замкнутой системы связана с устойчивостью разомкнутой.

Поскольку

, (5.10)

открываются возможности судить об устойчивости замкнутой системы по передаточной функции разомкнутой системы.

Запишем выражение (5.10) в частотной форме, полагая p = j :

1 + W(j) .

W(j) есть комплексная частотная характеристика разомкнутой системы. Эту характеристику можно изобразить графически на комплексной плоскости, задавая от 0 до ∞ и рассчитывая частотные характеристики: действительнуюU() и мнимуюV() . Получается годограф разомкнутой системы. Его вид говорит об устойчивости или неустойчивости замкнутой системы.

Допустим, разомкнутая система устойчива. Тогда, если годограф устойчивой разомкнутой системы при изменении  от 0 до ∞не охватывает точку -1 на оси абсцисс, то замкнутая система будет устойчивой. Охватывает – замкнутая система неустойчивая.

Примеры годографов, соответствующих устойчивой и неустойчивой замкнутой системам, представлены на рис. 5.14 и 5.15 .

V V

U

U

-1 -1

Рис. 5.14 Рис. 5.15

V V

-1 -1

U

U

Рис. 5.16 Рис. 5.17

V V

-1 -1

U

U

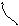
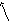
Рис. 5.18 Рис. 5.19

Замкнутая система может быть устойчивой и тогда, когда разомкнутая система неустойчива.

Критерий Найквиста для неустойчивой разомкнутой системы: если годограф неустойчивой разомкнутой системы при изменении  от 0 до ∞ охватывает точку -1 на оси абсцисс в положительном направленииm/ 2 раз, гдеm – число корней характеристического уравнения разомкнутой системы с положительной действительной частью, то замкнутая система будет устойчивой. (положительной считается движение конца вектора против часовой стрелки).

Примеры годографов, соответствующих устойчивой и неустойчивой замкнутым системам во втором случае, представлены на рис. 5.16 и 5.17 для m= 2 .

Если разомкнутая система имеет передаточную функцию, содержащую в знаменателе множителем комплексную переменную р ,

,

то комплексная частотная характеристика будет иметь неопределенность при  = 0 . Амплитуда становиться бесконечной. Годограф получается с бесконечной ветвью. Но если годограф мысленно дополнить зеркально отраженной ветвью и провести полуокружность бесконечно большого радиуса так, чтобы она пересекала положительную часть оси абсцисс, то такой прием позволяет использовать первую формулировку критерия Найквиста. То есть, если точка -1 на оси абсцисс лежит за пределами замкнутой кривой – замкнутая система устойчивая. Если охватывается кривой – неустойчивая. Примеры таких годографов приведены на рис. 5.18 и 5.19 .

Подведем итог сказанному в виде таблицы 1, с использованием соответствующих аббревиатур.

Таблица 1

РСУ . Тогда ЗСУ, если -1 вне.

ЗСН, если -1 внутри.

РСН . Тогда ЗСУ, если -1 вне.

ЗСН, если -1 внутри.

РС

астатическая. Тогда ЗСУ, если -1 вне.

ЗСН, если -1 внутри.

Замкнутая система будет находиться на границе устойчивости, если годограф разомкнутой системы проходит через точку -1 оси абсцисс. Аналитически это условие можно записать в виде

1 + W(j) = 0.

Кривые Найквиста наглядно показывают влияние коэффициента усиления на устойчивость системы. Для передаточной функции, в которой коэффициент усиления увеличивают, размеры и положение кривой Найквиста меняются относительно точки с координатой (-1,0). Допустим, имеется кривая 1, отвечающая границе устойчивости, рис.5.20. Предельный коэффициент усиления k=k^. Кривая 2, для которойkk^, отвечает устойчивой системе, кривая 3, для которой

kk^- неустойчивой. Увеличение коэффициента усиления вызывает смещение влево точки пересечения кривой 2 с отрицательной частью действительной оси. То есть, может перевести систему из устойчивого состояния в неустойчивое.

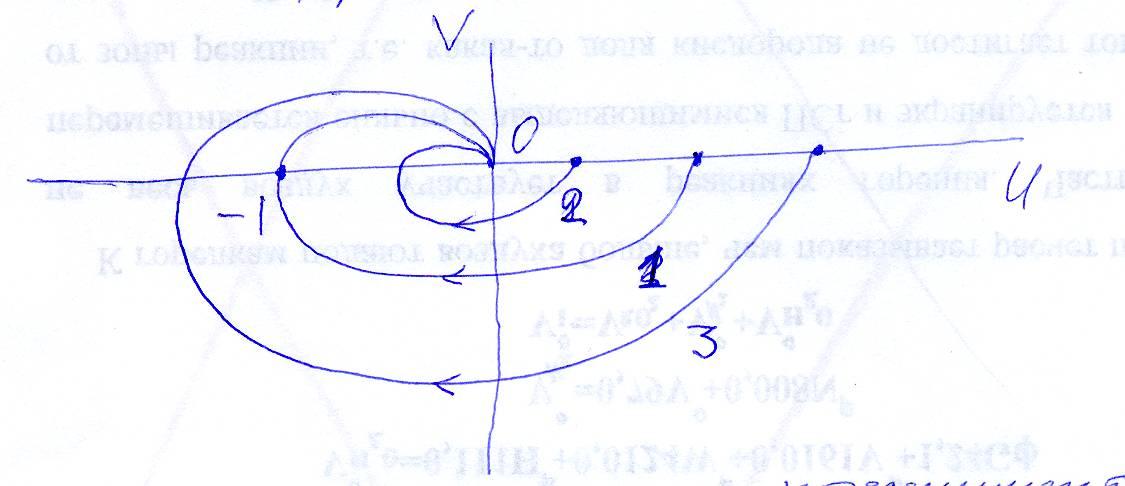
Рис. 5.20. Значение коэффициентов усиления:

1  k = k^, 2  k k^, 3 – k  k^.

Система, имеющая годограф, изображенный на рис. 5.20, с увеличением коэффициента усиления способна реализовать два состояния: «устойчивость – неустойчивость». Для более сложных кривых число состояний может увеличиваться. Например, у кривой с одним максимумом в отрицательной полуплоскости (рис. 5.21) по мере

Рис. 5.21 Рис. 5.22

увеличения коэффициента усиления устойчивое состояние сменяется неустойчивым, а затем снова устойчивым. У кривой с двумя максимумами (рис.5.22), при увеличении коэффициента усиления, реализуются состояния: «устойчивость – неустойчивость – устойчивость – неустойчивость». Система может устойчиво работать в двух разных интервалах изменения коэффициента усиления. Это свойство не обнаруживается применением критерия Гурвица или Михайлова.

Коэффициент усиления на границе устойчивости рассчитывают, приравнивая комплексную частотную характеристику минус единице:

W(j) = -1.

Пример 5.10.

Дана передаточная функция разомкнутой системы:

.

Полагая k = 2 проверить с помощью критерия Найквиста, будет ли устойчивой замкнутая система?

Предварительно выясняем устойчивость разомкнутой системы по критерию Гурвица: система устойчива.

Найдем комплексную частотную характеристику:

.

Выделим действительный и мнимый частотные полиномы:

,

.

Изменяя  от 0 до , построим годограф разомкнутой системы.

По условию V() = 0 находим частоты пересечения годографом действительной оси и соответствующие значения U():

V() = 0, 4 - ³ = 0, ₁ = 0, ₂ = 2,

U(0) = 2. U(2) = -0,18.

Полагая U() = 0, находим частоту пересечения годографом мнимой оси и соответствующее значение V():

U() = 0, 1-3² = 0, ,

V(0,58) = -3,7 .

Для  = 1 получаем U(1) = -0,3, V(1) = -0,46 .

При  =  U() = 0, V() = 0 .

Вид годографа показан на рис. 5.20.

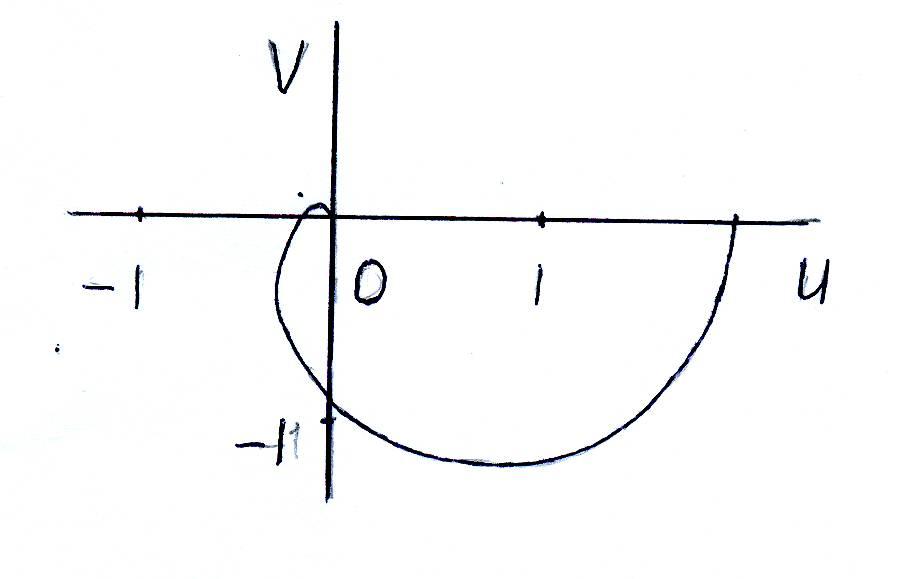
Рис. 5.20.

Разомкнутая система устойчивая, годограф не охватывает точку (-1,0), значит, замкнутая система тоже устойчивая.

Пример 5.11.

Система на границе устойчивости имеет передаточную функцию

.

Как зависит предельный коэффициент усиления k^ от параметров M и N?

Найдем комплексную частотную характеристику

.

Удовлетворив условию W(j) = -1, получаем два уравнения:

k^(N - ³) = 0,

k^(1 - M²) + (1 - M²)² + (N - ³)² = 0 .

Корни первого уравнения: ₁ = 0 и ₂ = .

Подставляя ₂ во второе уравнение, получаем:

k^ = MN – 1.

5.5. Выделение области устойчивости методом D - разбиения.

Устойчивость системы автоматического регулирования зависит от того, какими будут коэффициенты дифференциального уравнения, которое её описывает. Одна часть коэффициентов обеспечивает устойчивые решения дифференциального уравнения, другая часть – дополняющая первую - обеспечивает неустойчивые решения.

Идея метода D - разбиения заключается в том, чтобы найти границу между этими коэффициентами и тем самым указать область устойчивости. Для этого выделяют один или два важных коэффициента, изменяют их и исследуют, как меняются корни характеристического уравнения. Все остальные коэффициенты фиксируются.

Пусть дано характеристическое уравнение системы автоматического регулирования:

. (2.7.)

Пусть все коэффициенты заданы, кроме a₀ и a_n. Предположим, что уравнение (2.7.) имеет в плоскости корней k корней слева от мнимой оси и n - k корней справа для каких–то значений a₀ и a_n , рис. 5.21.

V p a₀

k n-k

D(k, n-k)

0 U

0 a_n

Рис. 5.21 Рис 5.22

Будем менять значения коэффициентов a₀ и a_n и находить корни. Возможно, для некоторой совокупности значений a₀ и a_n количество корней слева и справа от мнимой оси не меняется. Т. е. соотношение между k и n-k остается постоянным. Тогда как совокупность других значений коэффициентов a₀ и a_n меняет соотношение между k и n–k. Можно указать границу, отделяющую область постоянного отношения k и n - k. Эту область обозначают D(k , n - k), рис. 5.22.

Например, для характеристического уравнения четвертой степени

в плоскости коэффициентов могут быть следующие области:

D(0,4), D(1,3), D(2,2), D(3,1), D(4,0).

Всего n + 1 областей.

Из всех D(k, n - k) областью устойчивости будет только одна: D(n, 0). В ней все корни, располагающиеся слева от мнимой оси, имеют отрицательную действительную часть. Мнимая ось – граница устойчивости в плоскости корней. В плоскости коэффициентов кривая, отделяющая область устойчивости от области неустойчивости, будет ничем иным, как преобразованной мнимой осью.

5.5.1. D – разбиение по одному

параметру

Изучение метода D - разбиения начнем с выяснения влияния на устойчивость одного параметра. При заданных значениях других параметров. Обозначим параметр символом . Это может быть коэффициент характеристического уравнения, или сочетание коэффициентов. Например, в уравнении

Можно назвать параметром T₁, T₂, T₃, k.

Допустим, сделан выбор  = T₂. Тогда уравнение примет вид

(T₁²p³ + T₃p²) + T₁(k+1)p+k = 0 .

Полином, который умножается на  , обозначим Q(p), остальную часть S(p). Уравнение примет общий вид:

 Q(p) + S(p)=0 . (5.4)

Представив уравнение (5.4) в виде

, (5.5)

получаем как функцию переменнойp.

Чтобы построить границы области устойчивости, полагаем

p = j. Тогда (p) становится комплексным числом:

(jω) = -U(ω)+jV(ω) (5.6)

Если теперь задавать ω от 0 до +, вектор (jω) вычертит некоторую кривую на комплексной плоскости U, V. Эта кривая отображает на плоскость U, V мнимую ось комплексной плоскости корней, то есть будет границей, по одну сторону которой k корней, по другую n - k.

Если задавать ω от 0 до -, получится зеркальное отображение кривой для +ω. Поэтому кривую рассчитывают для положительных ω, а затем дополняют зеркальным отображением относительно действительной оси.

Чтобы разобраться, по какую сторону находятся k корней, область D - разбиения выделяется штриховкой. Соображения следующие.

При движении по мнимой оси в плоскости корней (рис. 5.23) от дота область, в которой находятся все корни устойчивости будет все время слева. Она показана штриховкой.

p

 +

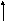V

Корни

устойчивости

0 U U

 -

Рис. 5.23. Рис. 5.24