
- •Предисловие
- •1.3. Принципы управления.
- •1.4. Задачи теории
- •Литература
- •2.1. Дифференциальное и операторное
- •2.3. Математические модели входных воздействий.
- •2.4. Переходная функция.
- •Литература
- •3.1 Усилительное звено.
- •3.2. Запаздывающее звено
- •3.3. Инерционное звено.
- •Построение выполняется по формуле
- •Вначале находим координаты пересечения:
- •Построение выполняется по формуле
- •Комплексная частотная характеристика
- •Логарифмическая амплитудная частотная характеристика
- •В случае 0,3 нужно пользоваться точной лачх из-за возрастания амплитуды в окрестности резонансной частоты.
- •3.7. Апериодическое звено второго порядка.
- •3.8. Классификация типовых звеньев.
- •Литература
- •4.1. Построение и анализ структурных схем.
- •4.1.1. Элементы структурных схем
- •4.1.2. Метод анализа структурной схемы
- •4.2. Передаточные функции систем
- •4.2.1. Последовательное соединение звеньев
- •Параллельное соединение звеньев.
- •4.2.3. Система с обратной связью
- •4.2.6. Передаточная функция по ошибке
- •4.2.7. Передаточная функция по возмущению.
- •4.2.8. Передаточные функции системы с перекрестными связями
- •4.3. Статические и астатические системы
- •4.4.2.1. Перенос узла через узел.
- •4.4.2.2. Перенос сумматора через сумматор.
- •4.4.2.3. Перенос сумматора через узел по направлению передачи сигнала
- •4.4.2.4. Перенос сумматора через узел против направления передачи сигнала.
- •4.4.3. Перенос узла или сумматора через звено.
- •4.4.3.1. Перенос узла с выхода звена на вход.
- •4.4.3.2. Перенос узла с входа звена на выход.
- •4.4.3.3. Перенос сумматора с выхода звена на вход.
- •4.4.3.4. Перенос сумматора с входа звена на выход.
- •5.1. Понятие об устойчивости.
- •Записываем операторное уравнение
- •5.2. Критерий Гурвица. Устойчивость системы по Гурвицу выясняется с помощью характеристического уравнения. Составляется специальный определитель – определитель Гурвица. Правило следующее.
- •5.3. Критерий Михайлова.
- •Находим передаточную функцию замкнутой системы
- •5.4. Критерий Найквиста
- •Если система замкнутая, ее передаточная функция
- •Требуется, чтобы и в плоскости область устойчивости находилась слева от кривойD-разбиения, если двигаться от к. Левая сторона кривой штрихуется.
- •Литература
- •6.1. Прямые показатели качества
- •6.2. Косвенные показатели качества
- •6.4. Апериодический процесс с колебательной составляющей.
- •Интегральные оценки качества. Первая интегральная оценка:
- •6.3. Чувствительность к изменению
- •Литература
- •7.1. Понятие синтеза системы.
- •2. Пропорционально-интегральный регулятор (пи-регулятор)
- •3. Пропорционально-дифференциальный регулятор (пд-регулятор)
- •1. Последовательная коррекция.
- •2. Параллельная коррекция.
- •3. Коррекция по возмущению.
- •Литература
- •Преобразование сигналов импульсным устройством
Требуется, чтобы и в плоскости область устойчивости находилась слева от кривойD-разбиения, если двигаться от к. Левая сторона кривой штрихуется.
Рассмотрим в качестве примера кривую, изображенную на рисунке 5.24. На этой кривой показано, как надо наносить штриховку. Область устойчивости ограничена кривой со штриховкой внутрь.
Параметр
![]() по физическому смыслу есть величина
действительная, поэтому для расчетов
используется только отрезок действительной
оси, охваченной кривыми со штриховкой
внутрь:
по физическому смыслу есть величина
действительная, поэтому для расчетов
используется только отрезок действительной
оси, охваченной кривыми со штриховкой
внутрь:
от точки 1 до точки 2. (рис. 5.24) .
П
Дано характеристическое уравнение:![]()
![]() .
.
Пусть
параметром будет
![]() ,
одно из значений которого
,
одно из значений которого![]() =1
проставлено в уравнении. Надо найти, в
каком интервале изменений
=1
проставлено в уравнении. Надо найти, в
каком интервале изменений![]() характеристическое уравнение отвечает
устойчивой системе автоматического
регулирования.
характеристическое уравнение отвечает
устойчивой системе автоматического
регулирования.
Из уравнения:
![]()
выделим: (p) = - p3 - p2 - p. Полагая p = j , находим:
![]() ,
,
![]() ,
,
![]()
Полагая V() = 0, найдем частоты и точки пересечения кривой с осью абсцисс: 1 = 0, U(0) = 0, 2 = 1, U(1) = 1. Неограниченно увеличивая выясним, что U и V , кривая уходит в бесконечность в верхней правой полуплоскости. В интервале 0 1 U 1 и V 0 . Для промежуточных значении U и V ход кривой уточняется заданием соответствующих частот. По совокупности данных строится кривая D-разбиения для положительных частот и дополняется зеркальным отображением. Наносится штриховка слева при движении по кривой от - к +.
Результат показан на рис. 5.25. Интервал устойчивых значений есть отрезок действительной оси от 0 до 1.
Контрольная проверка по критерию Гурвица для = 0,5.

0,5 1
Рис. 5.25
Записываем характеристическое уравнение:
p3 + p2 + p + 0,5 = 0 .
Коэффициенты: a0 = 1, a1 = 1, a2 = 1, a3 = 0,5. Действительно,
a1a2 -a0a3 > 0, система устойчива.
Пример 5.14.
Дано характеристическое уравнение вида:
![]() .
.
Требуется найти значения Т, при которых система будет устойчивой.
Назначив
Т
параметром, выделим
![]() :
:
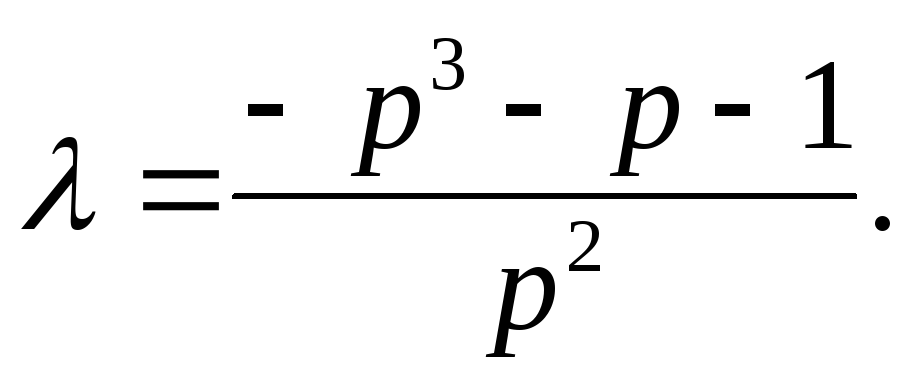
Полагая ![]() получаем:
получаем:
![]() .
.
Запишем действительную и мнимую части:
![]()
![]()
Анализ формул показывает:
- при = 0 U = , V = ;
- при = 1 U = 1, V = 0; кривая V (U) пересекает действительную ось;
при = U = 0, V = -;
Кривая начинается в + , пересекает ось абсцисс и неограниченно приближается к мнимой оси, уходя в .
Для уточнения хода кривой V (U) можно взять точки:
= 0,5, U = 4, V = 1,5.
= 2, U = 0,25, V = -1,5;
![]() , U
= 0,5 V
= -0,7;
, U
= 0,5 V
= -0,7;
= 0,82, U = 1,5, V = -0,4.
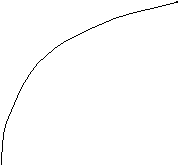
Построив на плоскости U, V кривую для положительных частот, отображаем ее зеркально относительно действительной оси и получаем кривую для отрицательных частот, рис. 5.26. Нанеся штриховку, получаем область устойчивости. Устойчивость системы обеспечивают те значения параметра , которые располагаются на отрезке действительной оси от 1 до . Контрольная проверка по критерию Гурвица подтверждает вывод.
 V
V
1,5
1
0,5
0
-0,5
-1
-1,5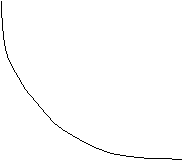
 1.5
1.5



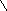



 1
1











 0.5
0.5











 2 3 4
U
2 3 4
U


 -0.5
-0.5












 -1
-1




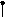
 -1.5
→
0
-1.5
→
0
→ + ∞
Рис. 5.26
П
Дано характеристическое уравнение вида
![]() .
.
Требуется найти интервал значений параметра λ, при которых САР будет устойчивой .
Записав
![]()
и положив p = jω , получаем комплексный параметр λ в виде
![]() .
.
Выделяем действительную и мнимую части:
![]() ,
, ![]() .
.
Задаем ω и рассчитываем U и V для построения кривой V (U):
-
ω
U
V
0
∞
-∞
2,36
9
-6,7
3,16
5
0
4
3,1
1,9
5
2
2,4
5,45
1,68
2,44
6
1,4
2,4
10
0,5
1,8
∞
0
0
Построив кривую для положительных , дополняем ее зеркально отображенной (для отрицательных ω). Результат показан на рис . 5.27 .
 V
V
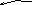 3
3











 2
=
0
2
=
0
=
∞












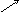

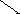




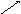









5







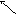 2U
2U
=
- ∞ 


















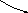 -2
= + 0
-2
= + 0

-3
Рис.5.27.
Вывод: САР устойчива при значениях λ, принадлежащих интервалу
0 5. Границе устойчивости отвечают λ = 0 и λ = 5 .
Контрольная
проверка по критерию Гурвица: все
коэффициенты характеристического
уравнения больше нуля, определитель
a1a2
- a0a3
> 0 .![]()
5.5.2. D - разбиение по двум параметрам.
В основе лежит допущение, что в характеристическом уравнении можно выделить два параметра, М и N, которые могут изменяться, а остальные параметры заданы. Параметром может быть коэффициент или комбинация коэффициентов.
Если параметры М и N входят в характеристическое уравнение линейно, то характеристическое уравнение может быть представлено в виде
MQ(p) + NR(p) + H(p)=0 , (5.7)
где Q, R, H – некоторые полиномы.
Выделение областей устойчивости в плоскости параметров N и М достигается следующей процедурой.
Подставляем в характеристическое уравнение p = jω. Полиномы Q, R, H распадаются на вещественные и мнимые части:
Q (jω) = Q1(ω) + jQ2(ω),
R (jω) = R1(ω) + jR2(ω),
H (jω) = H1(ω) + jH2(ω).
Теперь их надо ввести в характеристическое уравнение (5.7) и выделить действительные и мнимые слагаемые:
Q1(ω) М + R1(ω) N + H1(ω) + jQ2(ω) M + R2(ω) N + H2(ω) = 0.
Если комплексное выражение равно нулю, значит его действительное и мнимое слагаемые по отдельности равны нулю:
Q1(ω) M + R1(ω) N + H1(ω) = 0,
Q2(ω) M + R2(ω) N + H2(ω) = 0.
Получается два линейных уравнения для определения параметров M и N :
Q1(ω) M + R1(ω) N = -H1(ω),
Q2(ω) M + R2(ω) N = -H2(ω) . (5.8)
Величины Q1 , Q2 , R1 , R2 рассматриваются как коэффициенты, а М и N – как переменные.
Определитель системы
 .
.
Определители параметра М и параметра N:
 ,
, 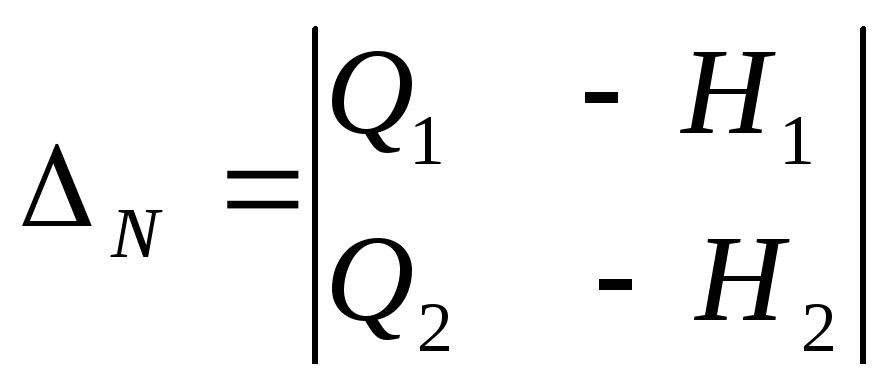 .
.
Определитель М получается из определителя системы заменой элементов первого столбца свободными членами системы. Определитель N – заменой элементов второго столбца свободными членами системы.
Для конкретного значения :
![]() ,
, ![]() .
.
На плоскости M, N это будет точка. Задавая ω от нуля до бесконечности, в плоскости M, N можно построить кривую, которая и есть граница D - разбиения. Система уравнений (5.8) имеет решение, если Δ ≠ 0 и ΔM 0, ΔN ≠ 0 ; и не имеет решения, если Δ = 0 (точка с координатами (M, N) уходит в бесконечность) . В случае Δ = 0, ΔM = 0, ΔN = 0, значения M и N становятся неопределенными. Уравнения (5.8) становятся зависимыми и определяют собой не точку, а прямую в плоскости M, N . Такая прямая называется особой прямой. В большинстве случаев особые прямые получаются для ω = 0 и ω = ∞.
Область устойчивости выделяется штриховкой. Правило штриховки следующее.
Если определитель Δ > 0, то двигаясь по D - кривой от ω = -∞ до ω = +∞, штрихуют левую сторону. Если Δ < 0 , то штрихуют правую сторону (знак определителя меняется, если + ω заменить на -ω).
Пример 5.16.
Дано характеристическое уравнение
p3 + Mp2 + Np + 1 = 0.
Произвести D - разбиение в плоскости параметров M и N.
Полагая p = jω, находим: -jω3 – ω2M + jωN + 1 = 0 .
Запишем для условий задачи систему уравнений (5.8). Если какой-то из полиномов Q1, Q2, R1, R2 окажется равным нулю, вместо него надо поставить ноль.
-ω2M + 0N +1 = 0 , -ω2M + 0N = -1,
или
0M + ωN - ω3 = 0 . 0M + ωN = ω3 .
Определитель
системы будет:
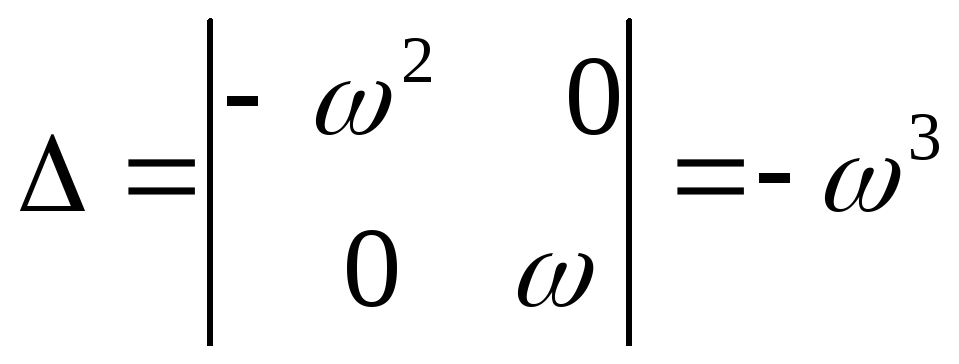 .
.
Определители параметров:
 .
.
 .
.
Получаем:
![]() ,
,
![]() .
Функциональная зависимость между
коэффициентамиM
и N
представляет собой равнобочную гиперболу:
MN
= 1. График
представлен на рис . 5.28 .
.
Функциональная зависимость между
коэффициентамиM
и N
представляет собой равнобочную гиперболу:
MN
= 1. График
представлен на рис . 5.28 .
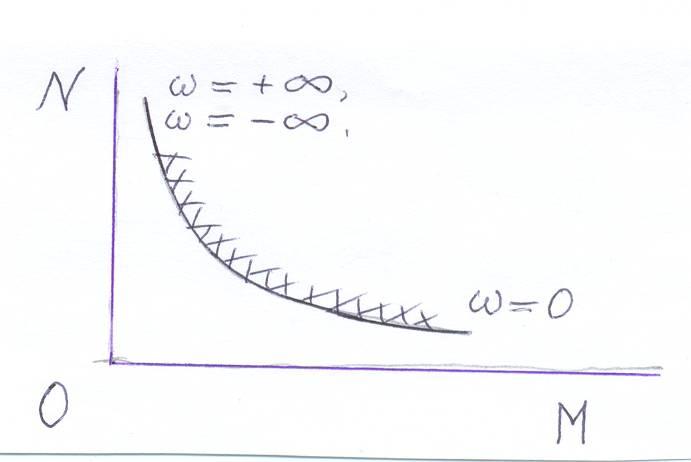
Рис. 5.28 .
Верхняя ветвь гиперболы уходит в как для положительных, так и для отрицательных значений ω. Нижняя ветвь гиперболы уходит в при стремлении к нулю положительных и отрицательных значений ω. Учитывая эти обстоятельства, штриховка получается двойной: < 0 при изменении ω от 0 до +∞ (штриховка справа) и > 0 при изменении ω от - до 0 (штриховка слева).
Пример 5.17.
Определить область устойчивости в плоскости параметров M и
N для уравнения:
p3 + Mp2 + Np + N + 1 = 0.
Полагая p = j, образуем частотное уравнение -j3 -2M+jN +N + 10 = 0. Записываем его действительное и мнимое слагаемые в виде системы двух уравнений:
-2M + N = - 10,
0M + N = 3 .
Составляем определитель системы
![]()
и определители параметров:
![]()
![]() .
.
Находим параметры:
![]() ,
N
= 2
,
N
= 2
При неограниченном возрастании частоты M стремится к 1, N стремится к бесконечности. При стремлении к нулю M стремится к бесконечности, N к нулю. Вид кривой Д-разбиения показан на рис. 5.29. Замена на - вида кривой не меняет.

Рис. 5.29.
Для значений 0 + определитель 0, штриховка наносится справа. Для - 0 определитель 0, штриховка слева. Получается двойная штриховка в сторону области устойчивости, рис. 5.29.
