1.4. Задачи теории

автоматического управления.

Основные задачи теории автоматического управления следующие:

- разработка методов анализа САУ;

- разработка методов синтеза САУ;

- разработка принципов построения и методов коррекции динамических свойств САУ.

Литература

1. Бесекерский В.А., Попов Е.П. Теория автоматического регулирования. – М.: Наука, 1974. – 992 с.

2. Ерофеев А.А. Теория автоматического управления. – СПб.: Политехника, 1998.

3. Востриков А.С., Французова Г.А. Теория автоматического регулирования. – М.: Высшая школа, 2004. – 365 с.

4. Попов Е.П. Теория линейных систем автоматического регулирования и управления. – М.: Высшая школа, 1989.

2.1. Дифференциальное и операторное

уравнения, передаточная функция и характеристическое уравнение разомкнутой системы.

Чтобы произвести расчет САУ, надо иметь математическую модель системы. Обычно математической моделью является дифференциальное уравнение, которое получают, анализируя физический, механический или иной процесс.

Рассмотрим математическую модель разомкнутой системы, которая выражается дифференциальным уравнением общего вида:

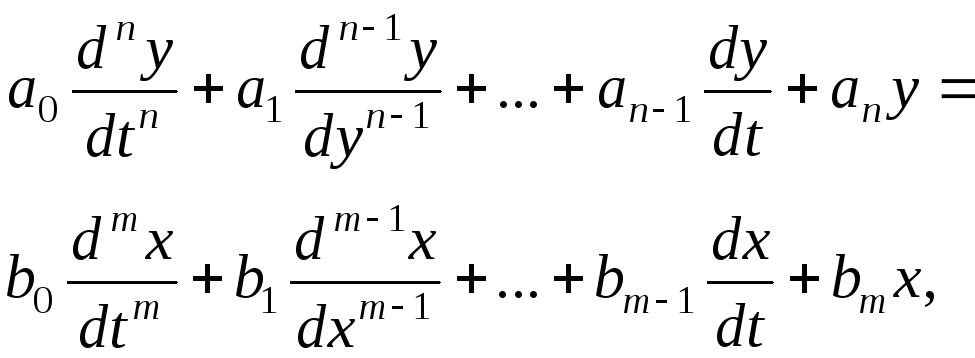(2.1)

где y – управляемая величина, x – управляющая величина; обе – функции времени; коэффициенты a_i, b_i – постоянные. Правая часть описывает воздействие, левая часть – изменение управляемой величины.

Решение уравнения (2.1) дает полное представление об изменении управляемой величины.

Однако в теории автоматического управления предпочитают иметь дело не с дифференциальным уравнением, а с операторным уравнением, точнее – с его особой формой, которая получила название «передаточная функция».

Операторное уравнение получают, применяя преобразование Лапласа к дифференциальному уравнению.

Суть преобразования Лапласа в том, что функцию от времени преобразуют в функцию от комплексного временного (-действительная часть,  - мнимая часть, j = ). Функцию от времени называют «оригинал», а ее преобразование по Лапласу – «изображение». Для изображения используют прописные буквы.

Символически преобразование Лапласа принято обозначать прописной буквой L. Например,

, ,.

(Читается: «изображение функции x(t) есть X(p)» и т. д.)

При преобразовании Лапласа коэффициентымножители не меняются, а изображение производной представляется произведением комплексного переменного p на изображение функции. Например,

, .

Более высокие производные представляются произведением p в соответствующей степени на изображение функции:

, и т. п.

Формально оператор дифференцирования заменяется комплексной переменной p в соответствующей степени:

на p , наp² , наpⁿ .

Преобразование Лапласа, будучи применено к дифференциальному уравнению, преобразует его в алгебраическое. Например,

.

Обратный переход из комплексного пространства во временное достигается обратными преобразованием Лапласа, символ L^-1 . Например,

, и т. д.

.

Дополнительно о преобразовании Лапласа рекомендуется прочитать в Приложении 1. В Приложении 2 дана таблица, показывающая преобразование Лапласа некоторых функций.

Применив преобразование Лапласа к дифференциальному уравнению общего вида (2.1) , получаем00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000

Или

(2.2)

Введем обозначения:

b₀p^m + b₁p^m-1 +…+ b_m-1 p + b_m = В(p) , (2.3)

a₀pⁿ + a₁p^n-1 +…+ a_n-1 p + a_n = D(p) . (2.4)

Комплексный полином В(р) описывает управляющее воздействие на систему. Комплексный полином D(p) описывает изменение управляемой величины. Введенные обозначения позволяют представить уравнение (2.2) краткой записью:

D(p) Y(p) = B(p) X(p).

Уравнение (2.2) и его краткую запись называют операторным уравнением.

Особую роль в математическом описании линейных систем автоматического управления играет отношение Y(p) / X(p). Его называют передаточной функцией и обозначают W(p).

. (2.5)

Уточним, что выражение (2.5) является передаточной функцией разомкнутой системы, поскольку получено из дифференциального уравнения (2.1) , записанного для разомкнутой системы.

Операторное уравнение можно записывать, используя передаточную функцию:

Y(p) = W(p) X(p). (2.6)

Как было сказано, комплексный полином D(p) описывает изменение управляемой величины. То есть, характеризует процесс, который происходит в системе под влиянием управляющего воздействия. Поэтому полином D(p) называют характеристическим. Приравнивая его к нулю, получают характеристическое уравнение системы:

a₀pⁿ + a₁p^n-1 + …+ a_n-1p + a_n = 0 . (2.7)

Характеристическое уравнение позволяет найти корни и получить решение дифференциального уравнения. Характеристический полином, характеристическое уравнение служат основой исследования системы на устойчивость.

Для преобразования Лапласа необходимо, чтобы начальные условия были нулевыми, а дифференциальные уравнения – линейными. Однако, линейность уравнений, описывающих реальные технические системы, скорее исключение, чем правило. В случае слабо нелинейной зависимости (типа слабо искривленной линии, участок которой можно заменить прямой с пренебрежимой погрешностью), осуществляют линеаризацию и ведут расчеты на отрезке прямой.

Пример 2.1.

Записать передаточную функцию и характеристическое уравнение для системы, поведение которой описывается дифференциальным уравнением

,

Производим замену символов в дифференциальном уравнении:

на p, p², p³ ;

y (t) на Y (p) ;

x (t) на X(p) .

Получаем операторное уравнение:

(2p³ + 6p² +10p +25) Y(p) = (3p² + 10p +100)X(p) .

Отношение Y(p) / X(p) есть передаточная функция W(p) . Значит, искомая передаточная функция есть

.

Комплексные полиномы имеют вид:

В(p) = 3p² + 10p + 100 ,

D(p) = 2p³ + 6p² + 10p +25 .

Характеристическое уравнение получается, если приравнять нулю комплексный полином знаменателя передаточной функции:

2p³ + 6p² + 10p + 25 = 0 .

2. Частотные характеристики.

Передаточная функция выражает свойства системы через комплексную переменную, которая содержит действительную и мнимую части: p =  + j. Мнимая часть имеет смысл циклической частоты колебаний. Если взять чисто мнимое значение комплексной переменной, p = j, и ввести эту величину в передаточную функцию (2.6), получается частотная функция:

. (2.8)

Ее называют комплексная частотная характеристика, амплитудно-фазовая частотная характеристика, комплексный коэффициент усиления.

По определению, она записывается отношением частотных полиномов. Но возможны и другие формы записи. Обратим внимание на то, что частотный полином В(j) в развернутом виде,

,

представляет собой сумму действительной и мнимой частей:

.

Так получается потому, что j = в четной степени будет либо –1, либо +1.

Частотный полином D(j) в развернутом виде имеет ту же структуру:

D(j) = D₁() + jD₂() ,

Следовательно комплексная частотная характеристика есть отношение двух комплексных чисел:

.

Умножение числителя и знаменателя на число, сопряженное знаменателю, позволяет выделить действительную и мнимую части:

.

Первое слагаемое обозначим U(), второе V(). U() называют действительной частотной характеристикой, V() - мнимой частотной характеристикой. В краткой записи

W(j) = U() + jV() . (2.9)

Комплексное выражение (2.9) можно интерпретировать геометрически, отложив по оси абсцисс действительную частотную характеристику, по оси ординат – мнимую частотную характеристику, рис. 2.1.

V()

М

A V



0 U U()

Рис. 2.1.

Для заданной частоты U() и V() – пара чисел, определяющих положение точки М на плоскости. Соединив прямой А начало координат с точкой М , получим прямоугольный треугольник. Для него справедливы соотношения: ,,

, . (2.10)

Все величины – функции частоты .

Комплексную частотную характеристику, следовательно, можно записать в виде

W(j) = U( ) + jV() = A ( cos () + j sin () ).

По формуле Эйлера . Поэтому

. (2.11)

А() называют амплитудной частотной характеристикой или просто амплитудой. () называют фазовой частотной характеристикой или просто фазой.

П

ример 2.2.

Записать комплексную частотную характеристику, частотные характеристики, амплитуду и фазу для системы, описываемой дифференциальным уравнением

.

Преобразуя по Лапласу, получаем операторное уравнение

(p² + 3p + 1) Y(p) = 2 X(p)

и передаточную функцию:

.

Подстановкой p = j превращаем передаточную функцию в комплексную частотную характеристику:

.

Действительная частотная характеристика

.

Мнимая частотная характеристика

.

Амплитуда

.

Фаза

.

П

ример 2.3.

Найти комплексную частотную характеристику, амплитуду и фазу пропорционально-интегрального регулятора (ПИ-регу-лятора). Его уравнение

.

(T – постоянная времени, k – коэффициент усиления).

Продифференцируем исходное уравнение,

и преобразуем по Лапласу:

.

Из операторного уравнения составим передаточную функцию:

.

Полагая p = j, записываем комплексную частотную характеристику

,

находим частотные характеристики:

U() = k , V() = -,

и амплитудную частотную характеристику:

.

Фаза в функции частоты имеет выражение

.

П

ример 2.4.

Найти логарифмическую амплитудную частотную характеристику ПИ-регулятора.

Воспользуемся выражением для амплитуды и запишем общий вид ЛАЧХ:

L() = 20 lg A() = 10 lg(k²T²² + 1) – 20 lg T .

Выделим асимптотические прямые.

В области  < 1 . С уменьшением  слагаемое k²T²² становится пренебрежимо меньше единицы. Его можно отбросить. Тогда первый член L() обращается в нуль вследствие lg 1 = 0. Остается

L₁ = - 20 lgT – 20 lg  .

В области > 1 . В первом слагаемом следует пренебречь единицей. В таком случае

L₂ = 20 lg k + 20 lg T - 20 lg T = 20 lg k.

Для построения графика надо найти точки пересечения прямой L₁ c осями координат и с прямой L₂ . (По ординате откладывают L₁, L₂, по абсциссе lg ).

Точка пересечения с осью ординат находится из условия lg  = 0. Получается: L₁ = -20 lg T = 20 lg (1/T).

Точка пересечения с осью абсцисс находится из условия L₁ = 0. Получается: lg = lg (1 / T) .

Точка пересечения прямой L₁ с прямой L₂ находится из условия L₁ = L₂ . Получается: lg  = lg (1 / kT) .

Вид графика показан на рис. 2.1.

Рис. 2.2. Асимптотическая логарифмическая

амплитудная частотная характеристика ПИ-регулятора