
- •I программа курса
- •II общие методические указания
- •III основные понятия курса
- •1. Элементы комбинаторики
- •2. Виды событий
- •3. Различные определения вероятности
- •Классическое определение вероятности
- •Статистическое определение вероятности
- •Геометрическое определение вероятности
- •4. Основные теоремы и формулы
- •Д) Исходя из того, что сумма событий состоит в появлении хотя бы одного из событий – слагаемых, в случае большого числа событий имеет смысл пользоваться другой формулой:
- •Формула полной вероятности
- •Формула Бейеса
- •IV. Повторные испытания
- •Формула Пуассона
- •Локальная теорема Лапласа
- •V. Случайные величины и их характеристики
- •1. Понятие о случайных величинах
- •2. Функции распределения
- •Свойства интегральной функции
- •Свойства дифференциальной функции
- •3. Числовые характеристики случайных величин
- •4. Конкретные законы распределения
- •5. Закон больших чисел
- •VI. Элементы математической статистики
- •1. Характеристики распределения опытных данных
- •2. Построение законов распределения по опытным данным
- •Построение нормального закона по эмпирическому вариационному ряду Пусть в результате испытания получен интервальный вариационный ряд признака
- •Вычисление теоретического ряда частот нормального распределения
- •Построение закона Пуассона по эмпирическому материалу
- •Пусть получен эмпирический вариационный ряд признака
- •Вычисление теоретического ряда частот распределения Пуассона
- •3. Критерии согласия. Основные понятия
- •Критерий согласия Пирсона
- •Критерий согласия Колмогорова
- •Критерии согласия Ястремского
- •Критерий согласия Романовского
- •4. Линейная корреляция и уравнение линейной регрессии
- •IV применение компьютерных средств для решения некоторых задач статистики
- •Ввод данных
- •Графическое представление данных
- •Статистический анализ данных в Excel
- •VIII. Задания для контрольной работы
- •I. Решить задачи
- •IV. Решить задачи
- •V. Для дискретной случайной величины х, заданной рядом распределения, найти:
- •VI. Непрерывная случайная величина х задана интегральной функцией
- •IX. В предположении о распределении признака по признаку Пуассона вычислить теоретические частоты, проверить согласованность теоретических и фактических частот на основе критерия Ястремского.
- •Приложение 1
- •Приложение 2
- •Продолжение приложения 2
- •Критические точки распределения
- •Значения (распределение Пуассона)
- •Критерий Колмогорова
- •Критерий Колмогорова
IV. Повторные испытания
Схема Бернулли – последовательность испытаний, удовлетворяющих условиям:
-
число испытаний
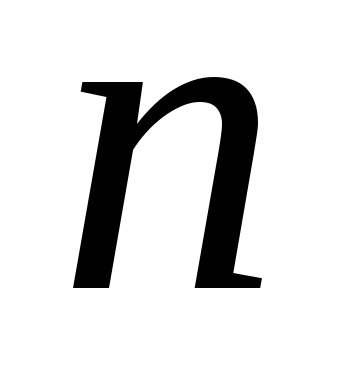 фиксировано,
фиксировано, -
каждое из испытаний приводит к одному из двух взаимоисключающих исходов,
-
вероятности этих исходов постоянны во всех испытаниях,
-
опыты независимы.
Пусть проведено
![]() независимых испытаний, в каждом из
которых событие
независимых испытаний, в каждом из
которых событие
![]() может появиться с постоянной вероятностью
может появиться с постоянной вероятностью
![]() .
Вероятность ненаступления события
.
Вероятность ненаступления события
![]() в каждом испытании равна
в каждом испытании равна
![]() :
:
![]() .
Требуется вычислить вероятность того,
что в
.
Требуется вычислить вероятность того,
что в
![]() независимых испытаниях событие
независимых испытаниях событие
![]() появится ровно
появится ровно
![]() раз:
раз:
![]() .
.
Формула Бернулли
Если вероятность
![]() появления события
появления события
![]() в каждом испытании постоянна, а число
испытаний невелико
в каждом испытании постоянна, а число
испытаний невелико
![]() ,
то вероятность того, что событие
,
то вероятность того, что событие
![]() при
при
![]() независимых испытаниях появиться ровно
независимых испытаниях появиться ровно
![]() раз, можно определить по формуле:
раз, можно определить по формуле:
![]() .
.
Вероятность того, что событие наступит
|
|
|
|
|
|
|
|
Формула Пуассона
Если число независимых
испытаний
![]() достаточно велико, а вероятность
достаточно велико, а вероятность
![]() появления события
появления события
![]() в каждом испытании очень мала
в каждом испытании очень мала
![]() ,
то вероятность появления события
,
то вероятность появления события
![]() ровно
ровно
![]() раз в
раз в
![]() испытаниях определяется по приближенной
формуле
испытаниях определяется по приближенной
формуле
![]() ,
,
![]() ,
,
![]() .
.
Локальная теорема Лапласа
Если вероятность
появления события
![]() в каждом испытании постоянна и равна
в каждом испытании постоянна и равна
![]() (причем
(причем
![]() не близко к 0 и 1), то вероятность того,
что событие
не близко к 0 и 1), то вероятность того,
что событие
![]() в серии из
в серии из
![]() независимых испытаний (где
независимых испытаний (где
![]() достаточно велико) появится ровно
достаточно велико) появится ровно
![]() раз, определяется по приближенной
формуле:
раз, определяется по приближенной
формуле:
![]() ,
,
![]() ,
,
где
![]() – функция вероятностей,
– функция вероятностей,
![]() – четная функция.
– четная функция.
Значения функции
![]() находят по таблице (приложение 1). Для
всех
находят по таблице (приложение 1). Для
всех
![]()
![]() .
.
Интегральная теорема Лапласа
Если число независимых
испытаний
![]() достаточно велико, а вероятность
достаточно велико, а вероятность
![]() появления события
появления события
![]() в каждом испытании не мала, то вероятность
появления события
в каждом испытании не мала, то вероятность
появления события
![]() в интервале от
в интервале от
![]() до
до
![]() раз определяется приближенной формулой
раз определяется приближенной формулой
![]() ,
,
![]() ,
,
![]() .
.
Функция
![]() – нечетная. Значения функции
– нечетная. Значения функции
![]() находят по таблице (приложение 2). При
находят по таблице (приложение 2). При
![]()
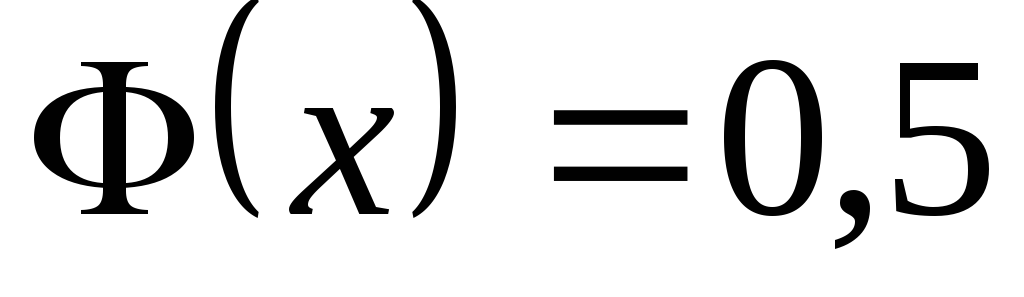 .
.
Вероятность
отклонения относительной частоты от
вероятности.
Пусть производится
![]() независимых испытаний, в каждом из
которых вероятность появления события
независимых испытаний, в каждом из
которых вероятность появления события
![]() постоянна. Вероятность того, что в
постоянна. Вероятность того, что в
![]() испытаниях относительная частота
появления события
испытаниях относительная частота
появления события
![]() отклонится от вероятности не более, чем
на
отклонится от вероятности не более, чем
на
![]() ,
определяется приближенной формулой
,
определяется приближенной формулой
![]() .
.
Наивероятнейшее
число появлений события в серии
независимых испытаний.
Число появлений
события
![]() в
в
![]() независимых испытаниях
независимых испытаниях
![]() называется наивероятнейшим,
если вероятность появления события это
число раз является наибольшей.
называется наивероятнейшим,
если вероятность появления события это
число раз является наибольшей.
![]() .
.
Если:
-
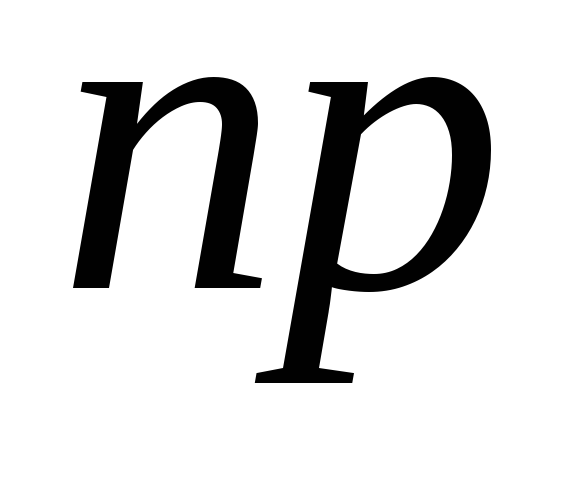 – целое число, то
– целое число, то
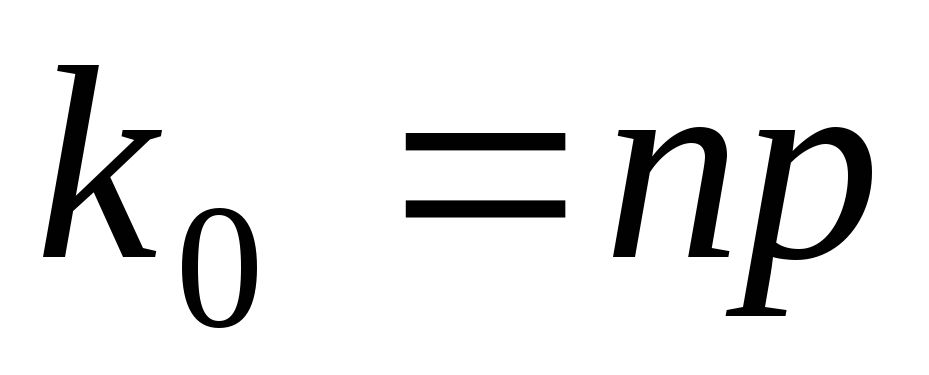 ,
, -
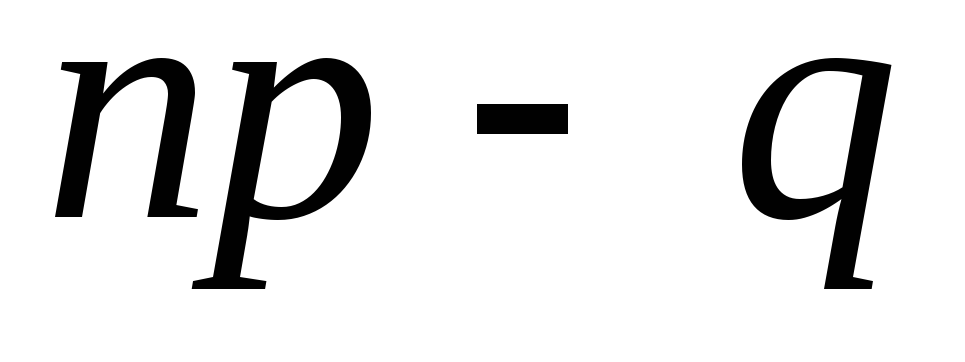 – дробное число, то
существует единственное число
– дробное число, то
существует единственное число
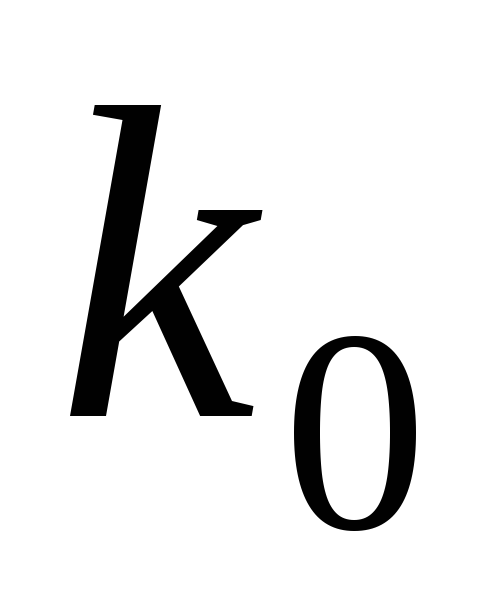 ,
равное целой части
,
равное целой части
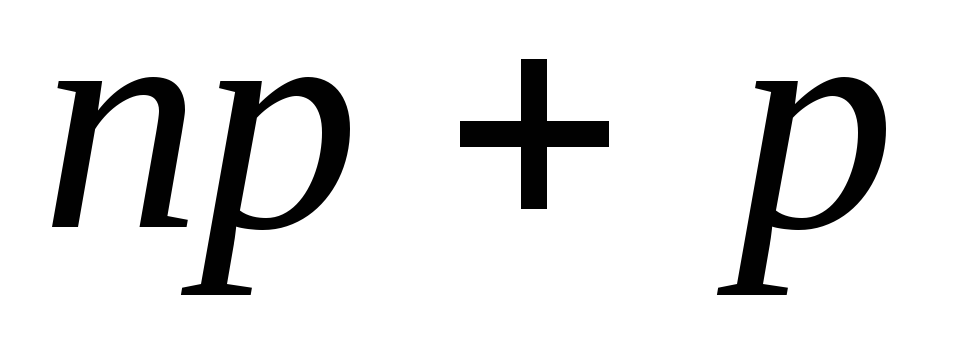 ,
,
-
 – целое число, то
существует два наивероятнейших числа,
равные соответственно левой и правой
части неравенства.
– целое число, то
существует два наивероятнейших числа,
равные соответственно левой и правой
части неравенства.
|
Пример 11. |
Вероятность попадания в мишень при одном выстреле равна 0,4. Найти вероятность 3-х попаданий при 5-ти выстрелах. |
Решение.
По формуле Бернулли определим искомую вероятность
![]() .
.
|
Пример 12. |
Учебник издан тиражом 100 000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0,0001. Найти вероятность того, что тираж содержит ровно 5 бракованных книг. |
Решение.
По условию
![]() .
.
Используем формулу Пуассона.
![]() ,
,
![]() .
.
|
Пример 13. |
75% всей продукции соответствует требованиям высшего сорта. Найти вероятность того, что в партии из 150 изделий: а) 100 изделий окажется высшего сорта; б) не менее 110 изделий окажутся высшего сорта. |
Решение.
а)
![]() .
.
Событие
![]() –
появление изделия высшего сорта.
–
появление изделия высшего сорта.
![]() .
.
По таблице (приложение 1) находим:
![]() ,
,
тогда
![]() .
.
б)
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
Значит
![]() .
.
|
Пример 14. |
Вероятность появления события в каждом из 625 независимых испытаний равна 0,8. Найти вероятность того, что относительная частота отклониться от 0,8 не более, чем на 0,04. |
Решение.
![]() .
.
![]() .
.
|
Пример 15. |
Вероятность того, что деталь стандартна, равна 0,9. Сколько необходимо проверить деталей, чтобы с вероятностью 0,9544 можно было утверждать, что частость отклониться от вероятности не более, чем на 0,02. |
Решение.
![]() .
.
![]() ,
,
![]() ,
,
по таблице
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
