§1.15. Реактивное движение. Уравнение Мещерского.

Реактивное движение основано на законе сохранения импульса.

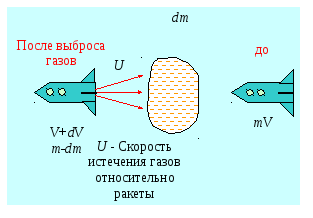
ракета газы до

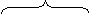
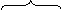
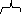
[(m - dm)( + d) + dm( + )] - , где - скорость истечения газов относительно ракеты. Тогда

+ (здесь опущены величины порядка )

Если на ракету действуют внешние силы, то , поэтому

+ или

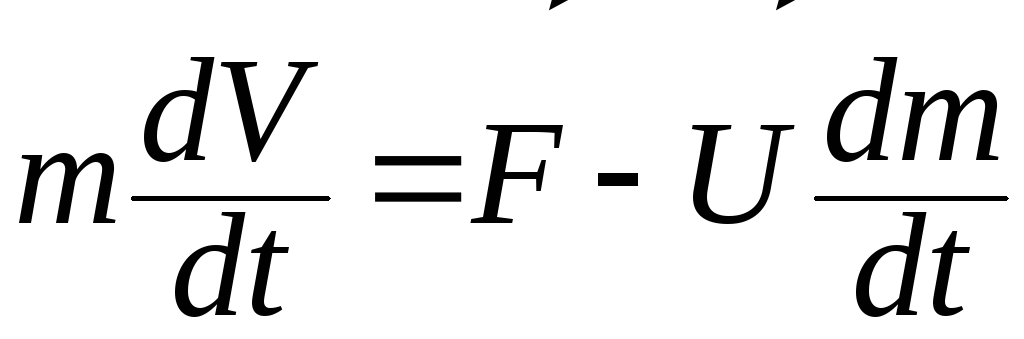
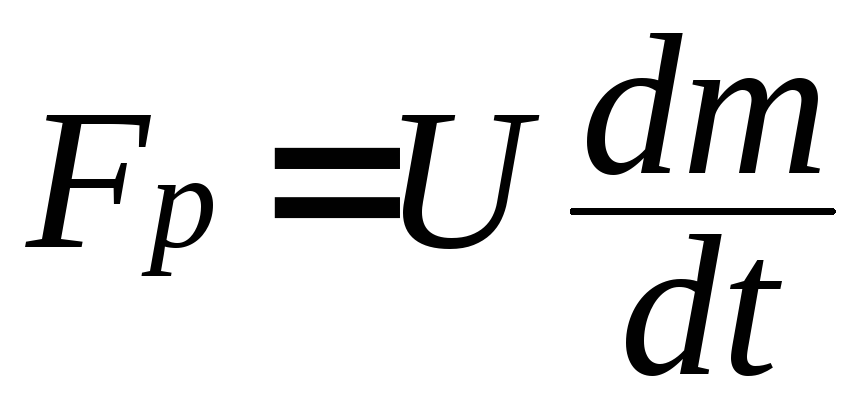- реактивная сила

Если противоположно по направлению, то ракета ускоряется, а если совпадает с , то тормозится. Окончательно уравнение движения тела переменной массы

+- уравнение Мещерского

Если внешних сил нет (F = 0), то

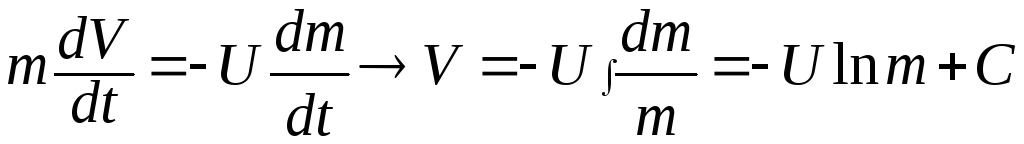
Значение постоянной интегрирования С определим из начальных условий. Если при t = 0 m = m₀ и V = 0, то С = U∙lnm₀. Следовательно,

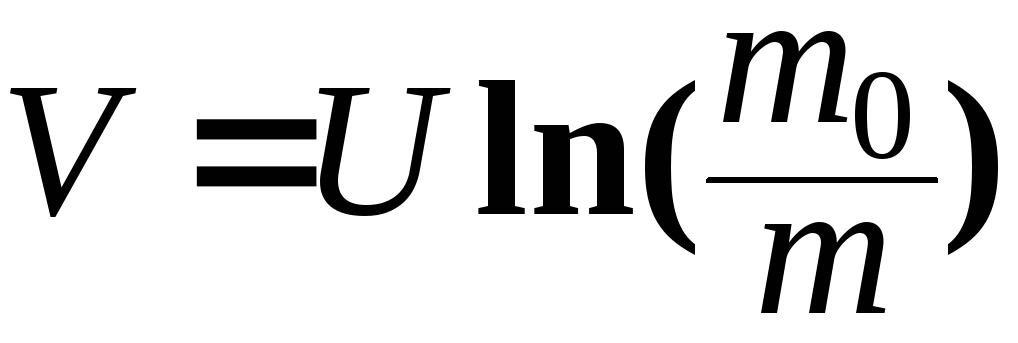- формула Циолковского

Она показывает, что:

1) чем больше конечная масса ракеты m, тем больше должна быть стартовая масса ракеты,

2) чем больше скорость истечения U газов, тем больше может быть конечная масса при данной стартовой массе ракеты.

Пример 1

Частица движется вдоль оси х по закону x = αt² – βt³, где α и β –положительные постоянные. В момент t = 0 сила, действующая на частицу, равна F₀. Найти значения силы F_x в точках поворота и в момент, когда частица опять окажется в точке х = 0.

Решение

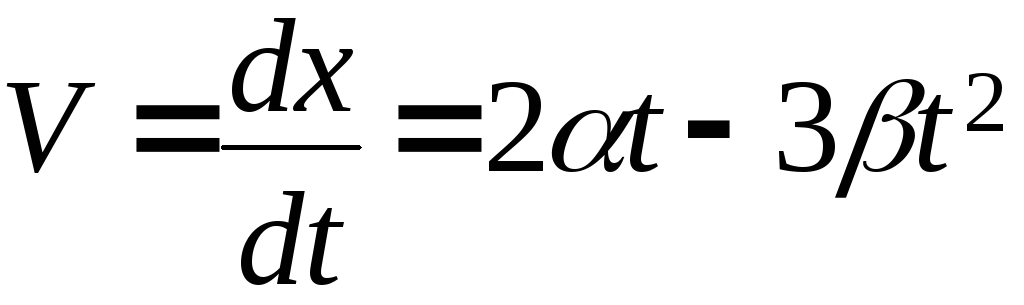
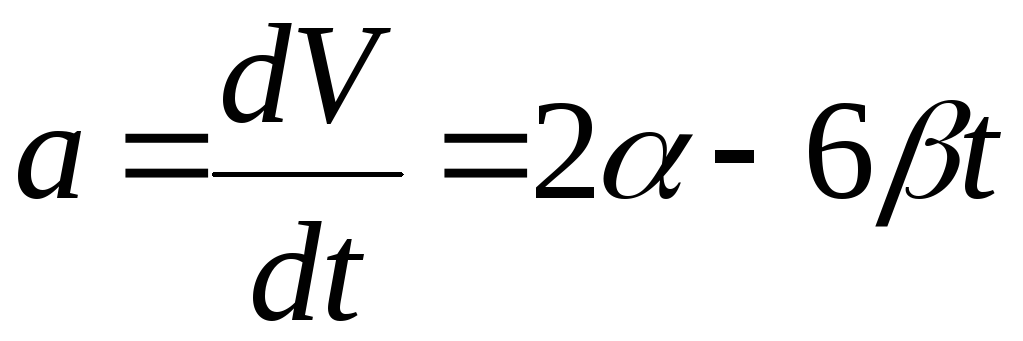, откуда , при t = 0 , будет , откуда 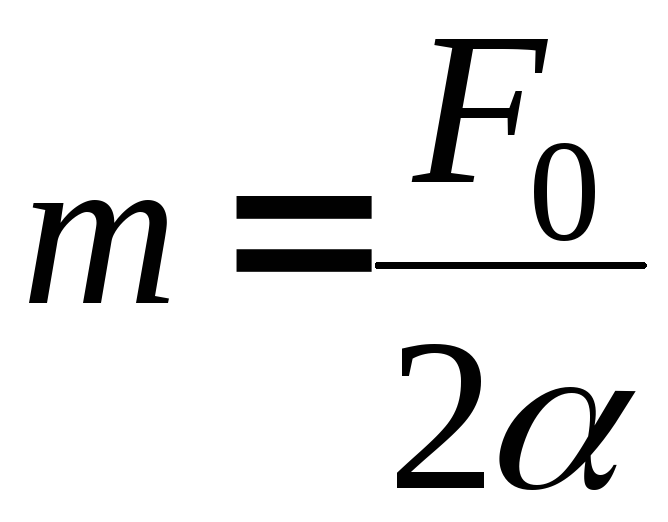. Время поворота найдём из условия, что в точке поворота , поэтому 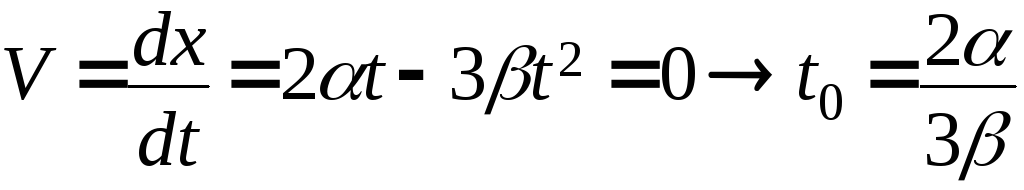- время поворота. Ускорение в этот момент времени будет , откуда сила, действующая в этот момент времени будет 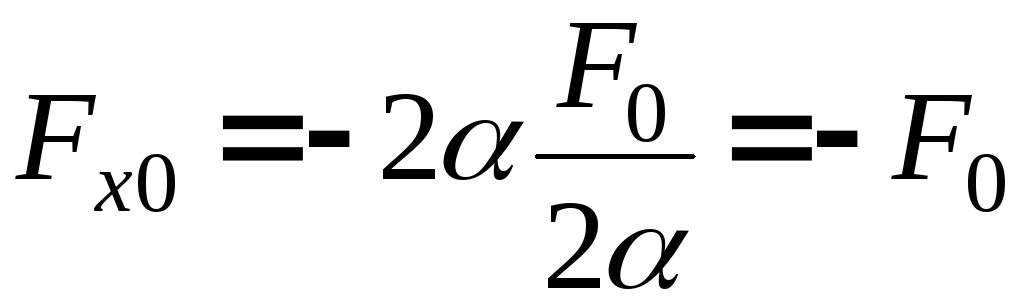- сила, действующая в точке поворота. Когда тело возвращается в исходную точку (х = 0), имеем:

αt² – βt³ = 0 → . В этот момент времени

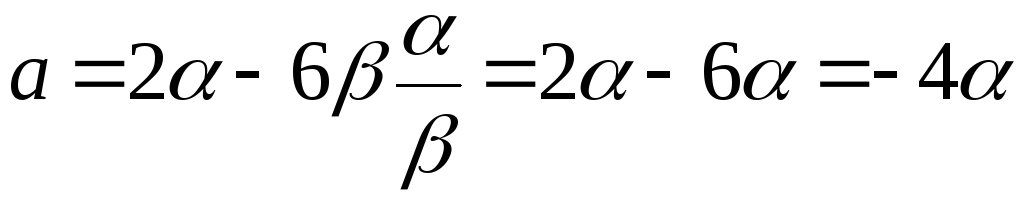
сила, действующая в этот момент времени

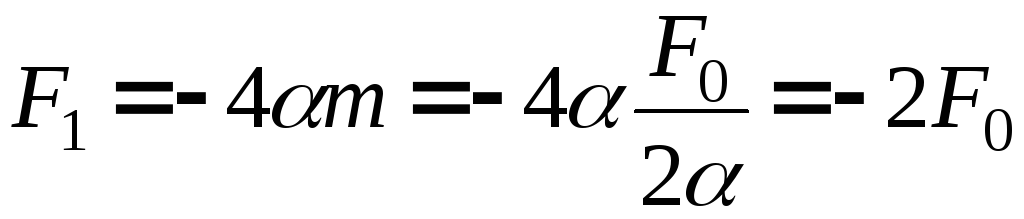
Итак, сила, действующая в точке поворота , сила, действующая в точке х = 0

Пример 2

Катер массы m движется по озеру со скоростью . В момент времени t = 0 выключили двигатель. Считая силу сопротивления пропорциональной скорости катера, , найти:

а)время движения катера с выключенным двигателем;

б)скорость катера в зависимости от пути, пройденного с выключенным двигателем, а также полный путь до остановки.

Решение

По II закону Ньютона , или

.

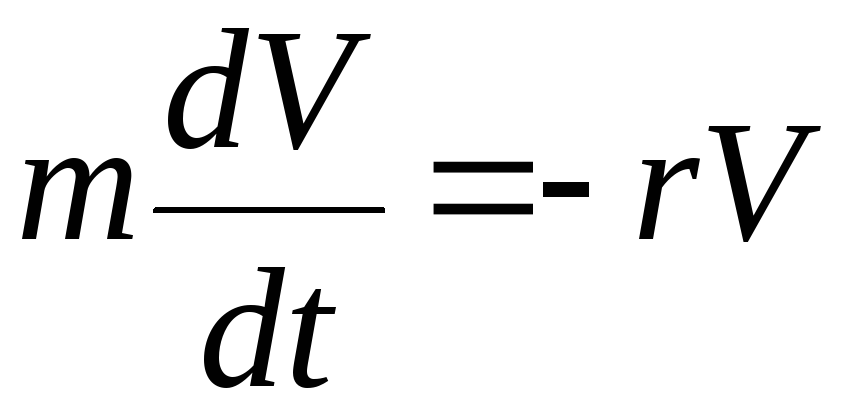Разделяя переменные, получаем

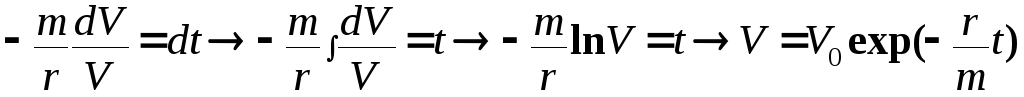
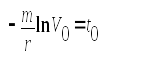
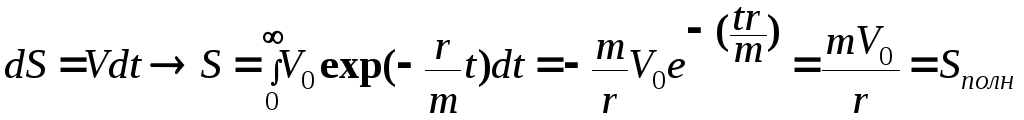
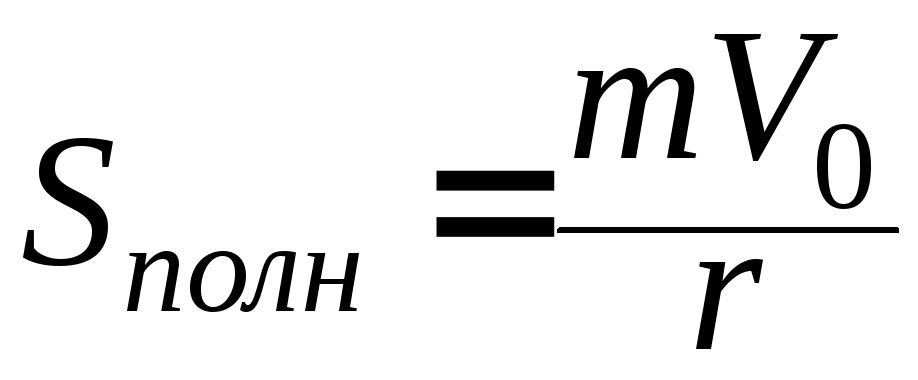
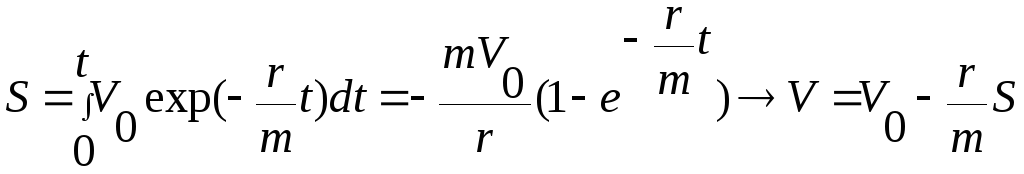
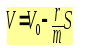
§1.16. Преобразование скорости и ускорения

при переходе от одной системы отсчёта к другой

В рамках ньютоновской механики длина и время считается абсолютными. Любой масштаб одинаков в разных системах отсчета, т.е. не зависит от движения. Течение времени также одинаково во всех системах.

Имеются две произвольные системы отсчета и , движущиеся относительно друг друга. Известны скорость V и ускорение а некоторой точки в К и ′- системе. Каковы соответствующие значения V′ и этой точки в -системе?

Рассмотрим три наиболее важных случая движения одной системы отсчета относительно другой.

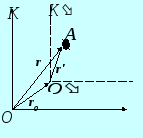
1.К^'-система движется поступательно по отношению к К-системе.

Пусть в К-системе начало отсчета К'-системы задаётся радиусом-вектром а её скорость и ускорение – векторами V₀ и Если положение точки А в К-системе определяется радиусом-вектором то

За промежуток времени точка совершит в К-системе перемещение

Откуда для преобразования скорости будет:

V = V₀ + V

Дифференцируя по времени, получаем:

При т.е. при движении К^'- системы без ускорения относительно К-системы, ускорения точки в обеих системах отсчета будут одинаковы.

2.К^'-система вращается с постоянной угловой скоростью вокруг оси, неподвижной в К-системе.

Возьмем начала отсчета К- и К^'-систем в произвольной точке О на оси вращения

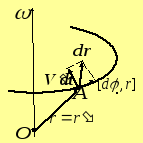
Тогда радиус-вектор точки А в обеих системах отсчета будет один и тот же:

Если точка А неподвижна в К^'-системе, то её перемещение в К-системе за время обусловлено только поворотом радиуса-вектора на угол (вместе с К^'-системой) и равно векторному произведению

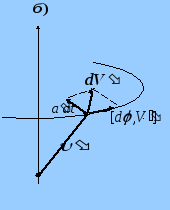
Если же точка А движется относительно К^'-системы со скоростью то за время она совершит дополнительно перемещение (рис.) и тогда

Разделив это выражение на получим формулу преобразования скорости:

,

где V и V′ скорости точки А в К- и К^'-системах отсчета соответственно.

В соответствии с (1) приращение вектора за время в К-системе должно складываться из суммы приращений векторов и т.е.

Если точка А движется в К^'-системе с то приращение этого вектора в К-системе обусловлено только его поворотом на угол (вместе с К^'-системой) и равно, как и в случае с векторному произведению Если же точка А имеет ускорение в К^'-системе, то за время вектор получит еще дополнительное приращение и тогда

Подставив всё в предыдущее равенство получаем формулу преобразования ускорения:

где и ускорения точки А в К- и К^'- системах отсчета. Второе слагаемое в правой части этой формулы называют кориолисовым (или поворотным) ускорением третье слагаемое – осестремительным ускорением

Таким образом, ускорение относительно К-системы равно сумме трех ускорений:

1. ускорения 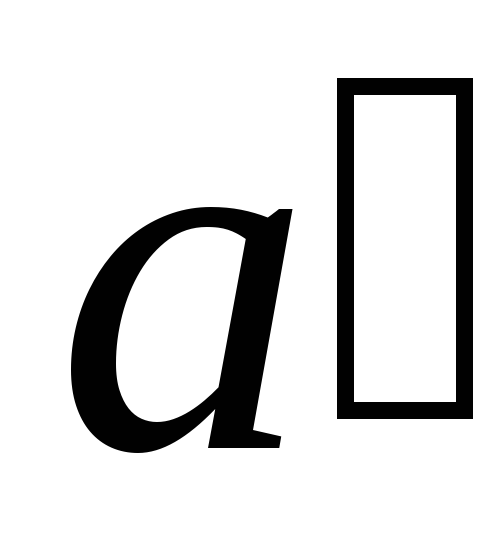относительно 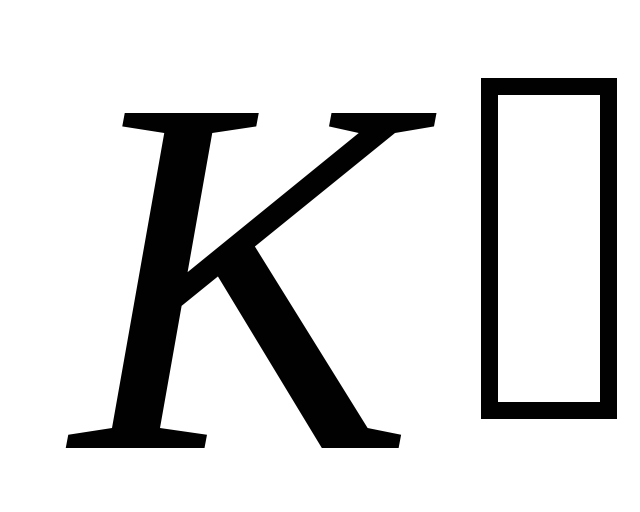-системы;

2. кориолисова ускорения ;

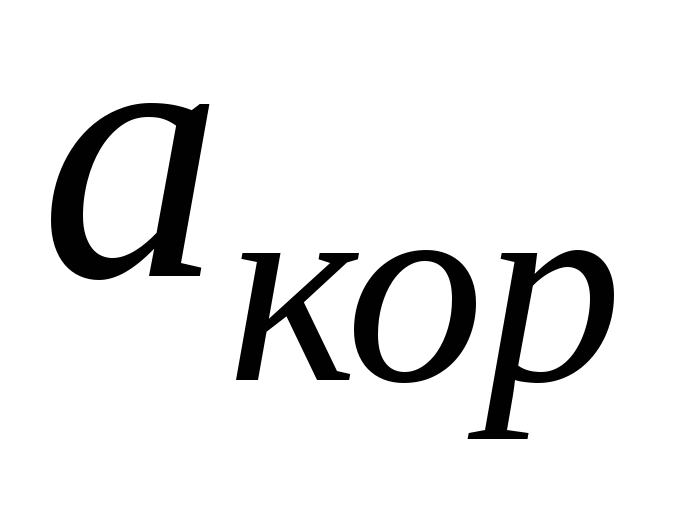3. осестремительного ускорения

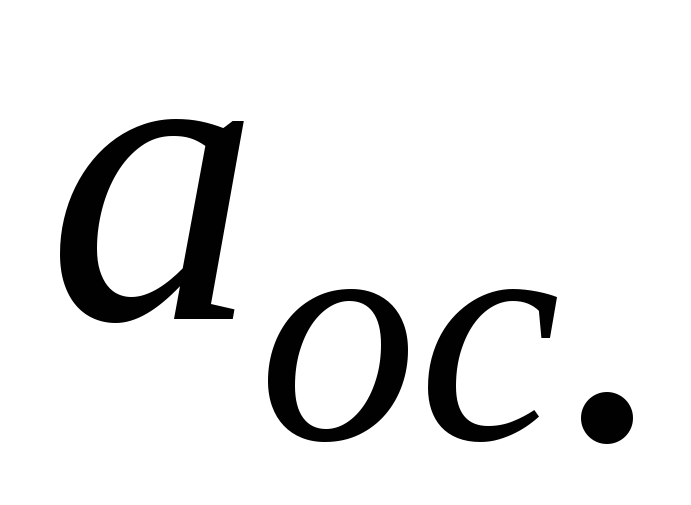
Осестремительное ускорение можно представить в виде где радиус-вектор, перпендикулярной оси вращения и характеризующей положение точки А относительно этой оси. Тогда формулу можно переписать так:

3.К^'- система вращается с постоянной угловой скоростью вокруг оси, перемещающейся поступательно со скоростью и ускорением по отношению к К-системе.

Этот случай объединяет два предыдущих. Введем вспомогательную S-систему отсчета, которая жестко связана с осью вращения К^'-системы и перемещается поступательно в К-системе. Пусть V и V_S скорости точки А в К и - системах отсчета, тогда

заменив V_S выражением где радиус-вектор точки А относительно произвольной точки на оси вращения -системы, получим следующую формулу преобразования скорости:

Аналогичным образом, найдем формулу преобразования ускорения:

В последних двух формулах V, V′ и скорости и ускорения точки А соответственно в - и -системах отсчета, V₀ и скорость и ускорение оси вращения К^'-системы в К-системе, радиус-вектор точки А относительно произвольной точки на оси вращения и характеризующий положение точки А относительно этой оси.

Пример.

Диск вращается с постоянной угловой скоростью вокруг собственной оси, укрепленной на оси. По диску движется точка А с постоянной относительно стола скоростью V Найдем скорость V′ и ускорение точки А относительно диска в момент, когда радиус-вектор, характеризующей ее положение по отношению к оси вращения, равен Скорость V′ точки А

Ускорение же найдем, учтя, что в данном случае ибо Тогда После подстановки в эту формулу для получим