§1.11. Современная трактовка законов Ньютона.

Первый закон Ньютона и понятие инерциальной системы отсчета.

1. Законы Ньютона – это система взаимосвязанных законов. Опытной проверке подвергается не каждый закон в отдельности, а вся система в целом.

Законы Ньютона в его формулировке выглядит так.

I закон. Всякое тело продолжает удерживаться в своём состоянии покоя или равномерного прямолинейного движения поскольку оно не понуждается приложенными силами изменить это состояние.

II закон. Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.

III закон. Действию всегда есть равное и противоположное противодействие, иначе – воздействия двух тел друг на друга между собою равны и направлены в противоположные стороны.

В кинематике выбор системы отсчета не был существенным. Все системы кинематически эквивалентны. В динамике это не так.

Поверхность Земли можно считать приблизительно инерциальной системой отсчета.

§1.12. Второй закон Ньютона как уравнение движения импульса.

Ускорение, приобретаемое телом, всегда прямо пропорционально равнодействующей приложенных сил:

~ (при m = const).

Кроме этого, для тел различной массы

a ~ (при F = const).

Учитывая эти выражения, имеем

- второй закон Ньютона.

Значение k зависит от выбора системы единиц. В СИ k = 1 и II закон Ньютона имеет вид

Заметим, что + +…+

В скалярной форме:

а_х= F_X=m

а_у= F_у=m

а_z= F_z=m

, но т.к. m=const её можно ввести под знак производной

но

откуда

- это более общая формулировка II закона Ньютона

В таком виде он применим и к движению тела переменной массы.

§1.13. Третий закон Ньютона.

Взаимодействие между материальными точками определяется III законом Ньютона: всякое действие материальных точек (тел) друг от друга носит характер взаимодействия, силы, с которыми действует друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки:

Эти силы приложены к разным точкам (телам), всегда действуют парами и являются силами одной природы.

§1.14. Закон сохранения импульса.

Закон сохранения импульса как фундаментальный закон природы.

Совокупность материальных точек (тел), рассматриваемых как единое целое, называется механической системой.

Силы взаимодействия между материальными точками механической системы называются внутренними.

Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними.

Система замкнута (или изолирована), если на нее не действуют внешние силы.

Если система состоит из многих тел, то по III з-ну Ньтона силы, действующие между этими телами, будут равны и противоположно направлены, т.е. геометрическая сумма внутренних сил равна нулю.

Можно показать, что 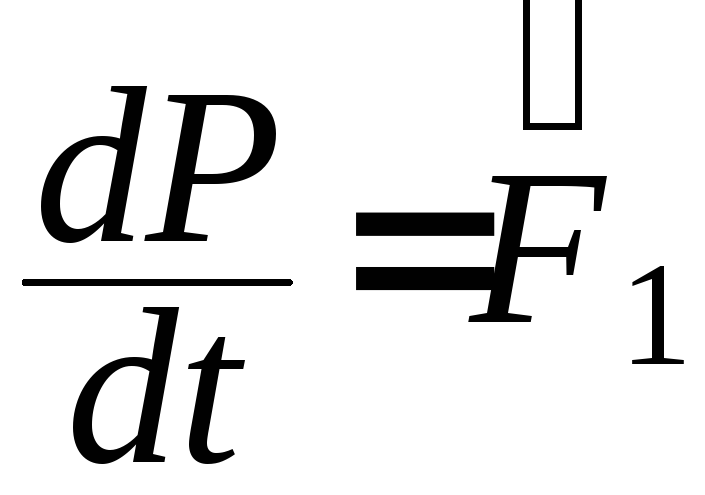+…+ где импульс системы

т.е. производная по времени от импульса механической системы равна геометрической сумме внешних сил, действующих на систему.

Если внешние силы отсутствуют (или их равнодействующая равна нулю)

Это – закон сохранения импульса: импульс замкнутой системы сохраняется, т.е. не изменяется с течением времени.

Этот закон справедлив на только в классической физике, хотя и получен как следствие законов Ньютона он справедлив и в квантовой механике, т.е. носит универсальный характер. Закон сохранения импульса – фундаментальный закон природы.

Закон сохранения импульса является следствием определённого свойства симметрии пространства – его однородности. Однородность пространства заключается в том, что при параллельном переносе в пространстве замкнутой системы тел как целого её физические свойства и законы движения не изменяются, т.е. не зависят от выбора начала координат инерциальной системы отсчета.

Импульс системы тел может быть выражен через скорость её центра масс. Центром масс (или центром инерции) системы материальных точек называется воображаемая точка С, положение которой характеризует распределение массы этой системы. Её радиус – вектор равен

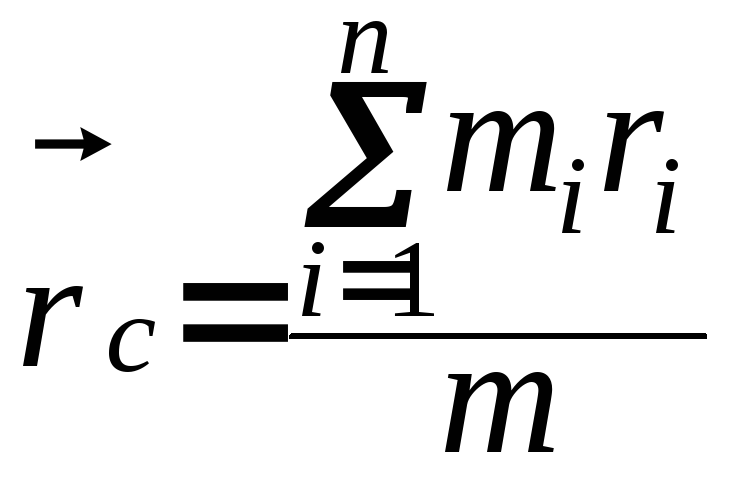где - масса системы.

Скорость центра масс

но импульс системы, откуда

++…+- закон движения центра масс.

т.е. центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, приложенных к системе. Если +…- равнодействующая всех сил, приложенных к системе, то

- импульс силы, т.е. изменение импульса системы равно импульсу силы, приложенной к системе (для незамкнутой системы).