
- •Глава I. Физические основы динамики.
- •§1.1. Предмет механики. Кинематика и динамика. Классическая механика. Квантовая механика. Релятивистская механика.
- •§1.2. Силы.
- •§1.3. Элементы кинематики.
- •§1.4. Пространство и время.
- •§1.5. Кинематическое описание движения.
- •§1.6. Вектор перемещения. Скорость. Ускорение.
- •§1.7. Движение точки по окружности.
- •§1.8. Линейная скорость точки.
- •§1.9. Связь между угловыми и линейными параметрами движения.
- •Решение:
- •§1.10. Элементы динамики поступательного движения. Основная задача динамики. Понятие состояния в классической механике. Масса, импульс, сила.
- •§1.11. Современная трактовка законов Ньютона.
- •§1.12. Второй закон Ньютона как уравнение движения импульса.
- •§1.13. Третий закон Ньютона.
- •§1.14. Закон сохранения импульса.
- •§1.15. Реактивное движение. Уравнение Мещерского.
- •Решение
- •Решение
- •§1.16. Преобразование скорости и ускорения
- •§1.17. Неинерциальные системы отсчета. Силы инерции.
- •§1.18. Силы инерции.
- •§1.19. Особенности сил инерции.
- •§1.20. Принцип эквивалентности.
- •§1.21. Закон сохранения энергии.
- •§1.22. Связь между кинетическими энергиями в различных системах отсчета.
- •§1.23. Энергия движения тела как целого.
- •§1.24. Потенциальная энергия.
- •§1.25. Законы сохранения и симметрия пространства.
- •§1.26. Графическое представление энергии.
- •§1.27. Элементы механики твердого тела.
- •§1.28. Момент инерции диска. Теорема Штейнера
- •§1.29. Момент силы
- •§1.30. Работа при вращательном движении.
- •§1.31. Момент импульса. Закон сохранения момента импульса.
- •§1.32. Условия равновесия твердого тела.
- •§1.33. Принцип относительности в механике. Инерциальные системы отсчёта и принцип относительности. Преобразования Галилея.
- •§1.34. Постулаты специальной теории относительности.
- •§1.35. Следствия из преобразований Лоренца.
- •§1.36. Элементы релятивистской динамики.
- •§1.37. Работа и энергия. Законы сохранения энергии и импульса.
- •§1.38. Механика колебаний и волн.
- •§1.39. Векторные диаграммы.
- •§1.40. Комплексная форма представления колебаний
- •§1.41. Сложение гармонических колебаний.
- •§1.42. Биения
- •§1.43. Кинетическая и потенциальная энергия при гармонических механических колебаниях.
- •§1.44. Гармонический осциллятор.
- •§1.45.Свободные и затухающие колебания.
- •§1.46. Вынужденные колебания осциллятора под действием синусоидальной силы.
- •§1.47. Волновые процессы.
- •§1.48. Эффект Доплера.
- •§1.49. Групповая скорость и её связь
- •§1.50. Одномерное волновое уравнение.
- •Глава II. Статистическая физика и термодинамика.
- •§2.1. Динамические и статистические закономерности в физике. Статистический и термодинамический методы.
- •§2.2. Макроскопические состояния.
- •§2.3. Уравнение состояния идеального газа.
- •§2.4. Давление газа с точки зрения молекулярно-кинетической теории.
- •§2.5. Молекулярно-кинетический смысл температуры.
- •§2.6. Статистические распределения.
- •§2.7.Скорости теплового движения частиц. Распределение частиц по абсолютным значениям скорости.
- •§2.8.Средняя кинетическая энергия частицы.
- •§2.9.Распределение Больцмана.
- •§2.10. Явления переноса. Понятие о физической кинетике.
- •§2.11. Эффективное сечение. Длина свободного пробега.
- •§2.12. Явления переноса.
- •§2.13. Теплопроводность.
- •§2.14. Диффузия.
- •§2.15. Внутреннее трение (вязкость).
- •§2.16. Основы термодинамики.
- •§2.17. Работа газа при изменении
- •§2.18. Эквивалентность теплоты и работы.
- •§2.19. Первое начало термодинамики.
- •§2.20. Теплоёмкость многоатомных газов.
- •§2.21. Применение первого начала термодинамики
- •§2.22. Работа в адиабатическом процессе.
- •§2.23. Энтропия.
- •§2.24. Изменение энтропии в изопроцессах.
- •4) Адиабатный.
- •§2.25. Связь энтропии с вероятностью состояния системы. Принцип возрастания энтропии.
- •§2.26. Свойства энтропии.
- •§2.27. Вычисление и применение энтропии.
- •§2.28. Цикл Карно.
- •§2.29. Второе начало термодинамики.
- •По Кельвину:
- •По Клаузиусу:
- •§2.30. Цикл Карно. Максимальный кпд тепловой машины.
- •§2.31. Фазовые равновесия и фазовые превращения. Фазы и фазовые превращения.
- •§2.32. Фазовые переходы I рода.
- •§2.33. Фазовые переходы II рода
- •§2.34. Условия равновесия фаз. Фазовые диаграммы.
- •§2.35. Метастабильные состояния.
- •§2.36. Реальные газы. Уравнение Ван-дер-Ваальса.
- •1) Учёт собственного объёма молекул.
- •2) Учёт притяжения молекул.
- •V метастабильные состояния Резюме
- •Оглавление
- •1.1. Элементы кинематики
- •1.2. Элементы динамики частиц
- •1.3. Законы сохранения импульса и механической энергии
- •1.4. Элементы механики твердого тела
- •1.5. Принцип относительности Галилея
- •1.6. Элементы релятивистской динамики
- •2. Механика колебаний и волн
- •2.1. Кинематика гармонических колебаний
- •2.2. Гармонический осциллятор
- •2.3. Волновые процессы
- •3. Статистическая физика и термодинамика
- •3.5. Реальные газы, жидкости и кристаллы
§1.50. Одномерное волновое уравнение.
Распространение волн в однородной изотропной среде в общем случае описывается волновым уравнением – дифференциальным уравнением в частных производных

или
 S
= S
(x,
y,
z,
t)
S
= S
(x,
y,
z,
t)
где V – фазовая скорость и
 оператор
Лапласа.
оператор
Лапласа.
Решением этого
уравнения является уравнение любой
волны.
 - дифференциальное уравнение плоской
волны.
- дифференциальное уравнение плоской
волны.
Резюме
-
 - уравнение бегущей
волны
- уравнение бегущей
волны -
 - эффект Доплера
- эффект Доплера -
 - фазовая скорость
- фазовая скорость -
 -
групповая
скрость
-
групповая
скрость -

-
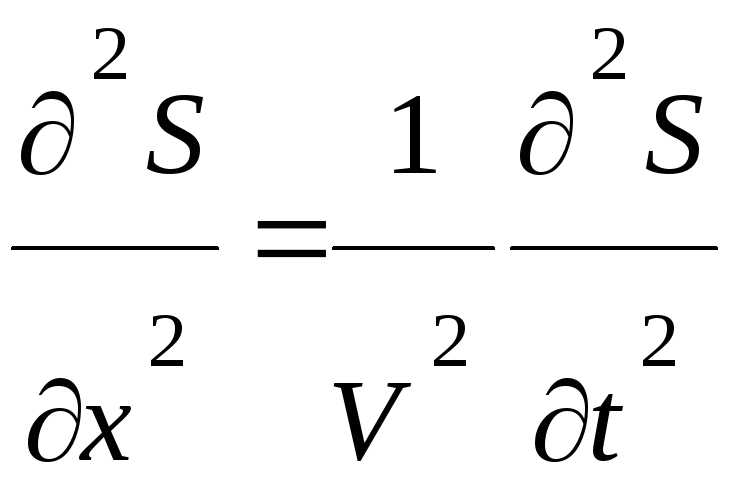 - уравнение плоской
волны
- уравнение плоской
волны
Л-10
Глава II. Статистическая физика и термодинамика.
§2.1. Динамические и статистические закономерности в физике. Статистический и термодинамический методы.
Статистический метод – основан на использовании теории вероятности и определенных моделей изучаемых систем.
Термодинамический метод – основан на анализе условий и количественных соотношений при различных превращениях энергии, происходящих в системе. Термодинамический метод не рассматривает внутреннее строение изучаемых тел и характер движения отдельных их частиц. Термодинамика – изучает общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия и процессы перехода между ними и не рассматривает микропроцессы, лежащие в основе этих превращений. Этим термодинамический метод отличается от статистического.
§2.2. Макроскопические состояния.
Тепловое движение. Макроскопические параметры.
Термодинамическая система – совокупность макроскопических тел, которые могут обмениваться энергией между собой и с внешней средой.
Величины, характеризующие состояние системы, называется параметрами состояния. Параметры состояния не всегда имеют определенное значение.
Неравновесное состояние – хотя бы один из параметров не имеет определённого значения.
Равновесное состояние – все параметры состояния имеют определённые значения, не изменяющиеся с течением времени.
Термодинамические системы, не обменивающиеся с внешней средой ни энергией, ни веществом называются изолированными или замкнутыми.
Процесс релаксации или просто релаксация – переход термодинамической системы в равновесное состояние.
Время, за которое первоначальное отклонение какой-либо величины от равновесного значения уменьшается в e раз, называется временем релаксации.
Термодинамический процесс – переход системы из одного состояния в другое. Всегда связан с нарушением равновесия системы.
Термодинамический процесс – равновесен, если в этом процессе система проходит непрерывный ряд бесконечно близких термодинамически равновесных состояний.
Чем медленнее реальный процесс изменения состояния системы - тем ближе он к равновесному, поэтому равновесные процессы называют квазистатическими.
Макроскопические термодинамические параметры делятся на : экстенсивные и интенсивные.
Экстенсивные параметры – пропорциональны количеству вещества в данной термодинамической системе (например, объём).
Интенсивные параметры - не зависят от количества вещества в системе (например, Т температура).
Внешние параметры системы – физические величины, зависящие от положения в пространстве и свойств тел, которые являются внешними по отношению к данной системе (например, для газа это объём V).
Внутренние параметры системы – физические величины, зависящие как от положения внешних по отношению к системе тел, так и от координат и скоростей частиц, образующих данную систему (например, для газа - Р и Т).
