§1.42. Биения

Пусть А₁ = А₂ = А, а частоты складываемых колебаний незначительного различаются, т.е. ω₁ = ω ω₂ = ω + ∆ω

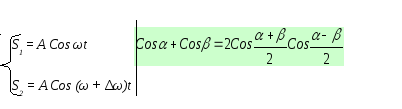
Учитывая, что < < ω получаем

Т.к. ∆ω << ω, то сомножитель, стоящий в скобках, почти не меняется, когда сомножитель Cos ωt совершает несколько полных колебаний. Результирующее колебание S можно рассматривать как гармоническое с частотой ω, амплитуда А_б которого меняется по закону

А_б =

Частота изменения А_б в 2 раза больше частоты изменения косинуса. Такие колебания называются биениями. Они возникают при сложении двух гармонических колебаний с близкими частотами. Частота биений равна разности частот складываемых колебаний ω_б = ∆ω = |ω₂ – ω₁|. Период биений

Т_б =

§1.43. Кинетическая и потенциальная энергия при гармонических механических колебаниях.

V = x = A Sin (ωt + φ0)

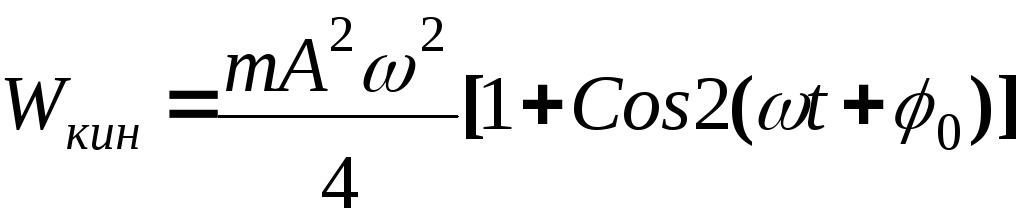
W = W_пот + W_кин =

Cos 2α = 1- 2 Sin2α = 2 Cos2α – 1

Резюме

• S(t) = A Sin (ωt + φ₀)

• Скорость

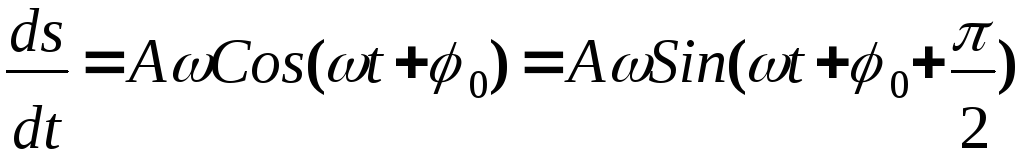
• Ускорение

• - дифференциальное уравнение гармонических колебаний

• А_б = - амплитуда биений

• 

• 

• 

Л-8

§1.44. Гармонический осциллятор.

Маятник, груз на пружине.

Физический маятник – твердое тело, которое может вращаться под действием своей силы тяжести mg вокруг неподвижной горизонтальной оси О, не проходящей через центр тяжести тела и называемой осью качания маятника.

d – расстояние от оси до центра масс,

то ,

где I – момент инерции маятника. При малых углах Sin α ≈ α, дифференциальное уравнение гармонических колебаний.

Его решение α = α₀ Sin (ωt + φ₀),

где

период колебаний физического маятника.

Математический маятник – материальная точка подвешенная на невесомой нерастяжимой нити и совершающая колебания в вертикальной плоскости под действием силы тяжести. Для него d = ℓ, где ℓ - длина нити, I = mℓ², откуда

Период колебаний физического маятника зависит от амплитуды колебаний α₀

Изменение значения Т при увеличении α₀ до 15º не превосходит 0,5%

Пружинный маятник

дифференциальное уравнение гармонических колебаний, его решение x = A Sin (ωt + φ₀)

где

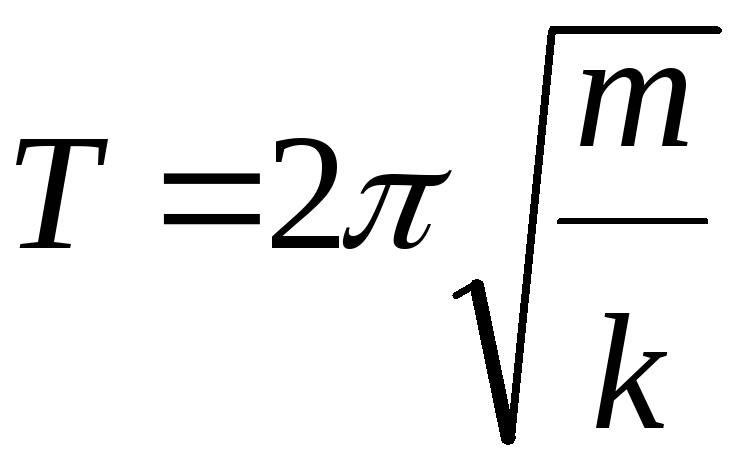
§1.45.Свободные и затухающие колебания.

Свободные затухающие колебания – колебания, амплитуда которых с течением временем уменьшается из-за потерь энергии реальной колебательной системой.

Свободные колебания – колебания в колебательной системе, без внешнего воздействия.

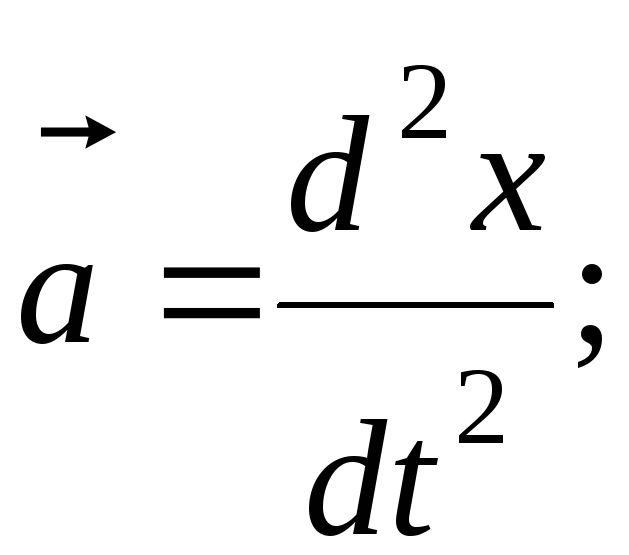
сила сопротивления,

b - коэффициент сопротивления,

дифференциальное уравнение затухающих колебаний.

(*)

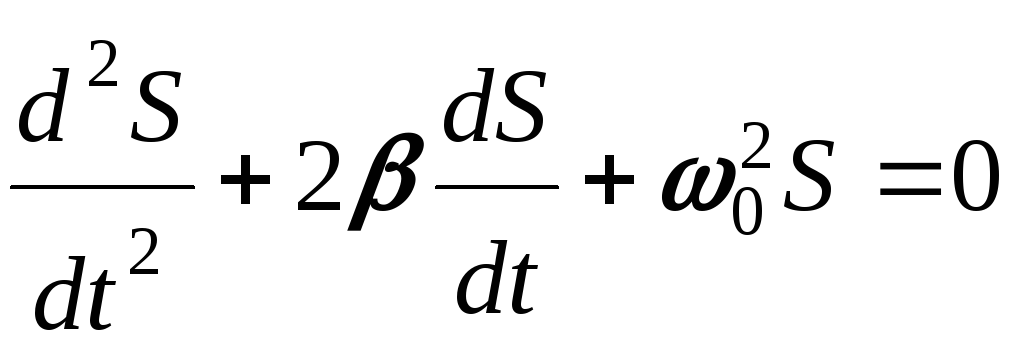где S – изменяющаяся при колебаниях физическая величина.

β – коэффициент затухания.

ω₀ – циклическая частота свободных незатухающих колебаний (т.е. при β = 0 ).

Решение этого уравнения

, (* *)

общее решение ,

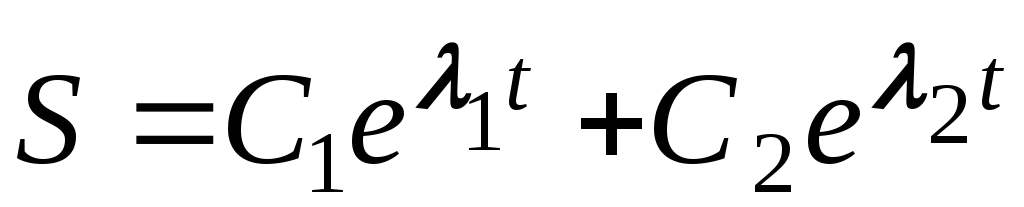где С₁ и С₂ – постоянные коэффициенты, зависящие от условий;

λ₁ и λ₂ – корни характеристического уравнения, получающегося из * подстановкой в него * *

Если β < 0, то корни этого уравнения комплексные

λ_{1, 2} = - β ± β ± iω

где

Общее решение:

или на основании формулы Эйлера

Вводя вместо С₁ и С₂ две новые постоянные А₀ и φ₀

А₀ Sin φ₀ = C₁ + C₂

i(C₁ – C₂) = A₀ Cos φ₀

и окончательно

Постоянные А₀ и φ₀ зависят от начальных условий, т.е. от значений S и в начальный момент времени.

Затухающие колебания, строго говоря, не являются периодическими, т.к. максимальное значение колеблющейся величины S достигаемое в некоторый момент t₁ в последующем никогда не повторяется

период (условный период) затухающих колебаний.

время релаксации (амплитуда колебаний уменьшается в e раз)

δ = логарифмический декремент затухания.

N – число колебаний, в течение которых амплитуда уменьшается в e раз

т.к. 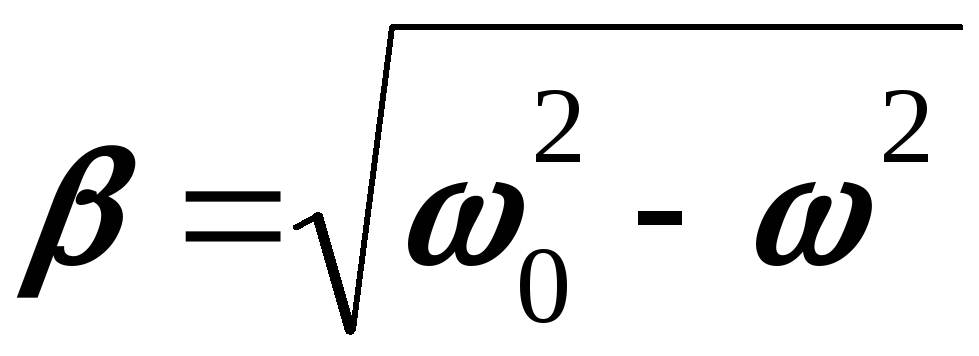и то

δ = βT = и

Добротность Q – величина, равная 2π, умноженная на отношение энергии W(t) колебательной системы в момент времени t к убыли этой энергии за один период

W(t) ~ A² →

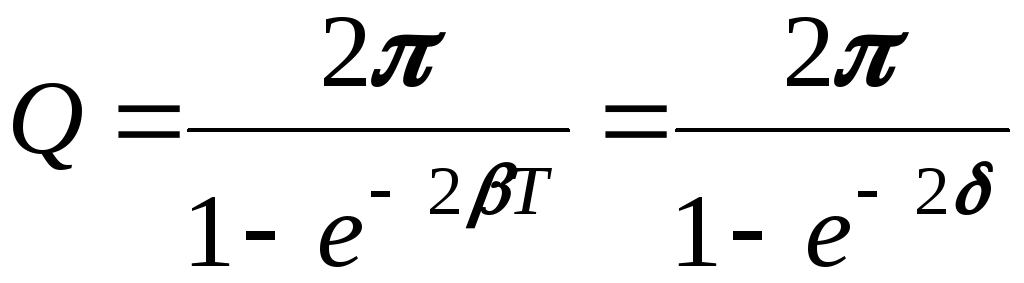
При малых значениях логарифмического декремента затухания

(δ << 1) ≈ 2δ и

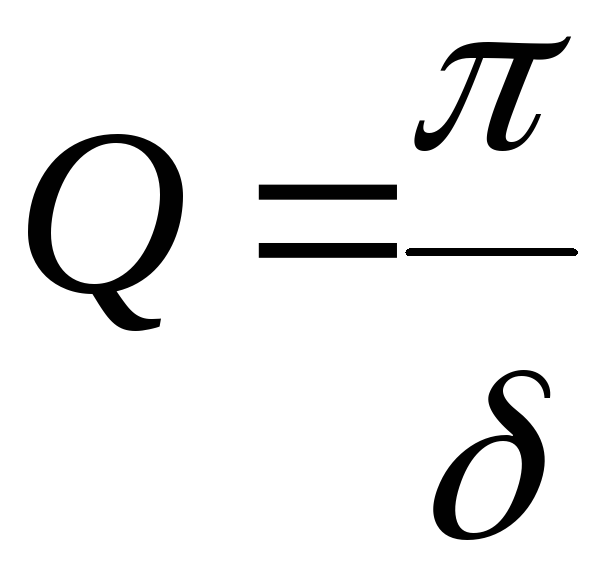
при этом ω ≈ ω₀ →

При β = ω₀ T→ ∞ и процесс становится апериодическим (т.е. колебаний не возникает).