1.3. Приведение произвольной системы сил к простейшему виду

Произвольная система сил может быть приведена к двум величинам: главному вектору , т.е. геометрической сумме сил системы, и главному моменту относительно некоторого центра , т.е. к геометрической сумме векторов моментов всех сил, составляющих систему. Последнее выражение может быть переписано в виде , где – радиус-вектор i-й силы относительно выбранного центра (точки О); n – число сил в системе.

Модуль главного вектора

,

где – сумма проекций всех сил системы соответственно на оси – проекции на оси координат i-й силы системы.

Модуль главного момента системы сил относительно некоторого центра

,

где – моменты всех сил системы относительно соответствующей оси координат.

Направления в пространстве главного вектора и главного момента определяются их направляющими косинусами:

 для главного вектора

; ; ;

 для главного момента

; ;

при соблюдении условия .

Рассмотрим возможности приведения различных произвольных систем сил к простейшему виду:

 если , система приводится к одной равнодействующей силе, линия действия которой проходит через центр приведения;

 если , система приводится к равнодействующей паре, момент которой является свободным вектором;

 если , эта система приводится к одной равнодействующей силе, равной главному вектору и приложенной в точке, отстоящей от центра приведения на расстояние ;

 если , система приводится к силовому винту (динаме), т.е. к совокупности силы и пары сил, плоскость действия которой перпендикулярна линии действия силы. Если угол  между векторами и меньше , то силовой винт называется правым, при – левым. При этом момент пары сил в составе динамы равен ;

 если , силы системы взаимно уравновешены.

Пример 1.3. По ребрам призмы действуют силы Р₁ = 40 Н, Р₂ = Р₅ = = 10 Н, Р₃ = 15 Н, Р₄ = 5 Н (рис.1.28). Кроме того, дано ОА = ОК = 20 см,  = 30. Привести эту систему сил к простейшему виду.

Решение. Выберем систему координатных осей (рис.1.28) и найдем проекции главного вектора на координатные оси:

;

;

.

Модуль главного вектора Следовательно, главный вектор направлен по оси y и равен  Н.

Приводя данную систему сил к началу координат, найдем проекции M_Оx, M_Оy, M_Оz на оси x, y, z главного момента относительно точки О.

Проекция на ось х . Так как силы , , пересекают ось x, а сила параллельна этой оси, то моменты этих сил относительно оси x равны нулю и, следовательно, . Сила лежит в плоскости zOy, причем наблюдатель, смотрящий со стороны положительного конца оси x, видит силу , действующую относительно точки О по часовой стрелке, поэтому

 Нм.

Проекция главного момента на ось y . Силы , , пересекают ось y, поэтому их моменты относительно этой оси равны нулю. Следовательно, . Так как силы и лежат в плоскости zx,  Нм и  Нм. Таким образом,

.

Так как силы , , , пересекают ось z, сила параллельна этой оси, а потому момент каждой из этих сил относительно оси z равен нулю, то

.

Итак, главный момент направлен вдоль оси x, и модуль его

 Нм.

Это означает, что данная система сил эквивалентна силе приложенной в точке О, и паре сил с моментом .

Остается теперь выяснить, к какому простейшему виду можно привести данную систему сил. Так как главный вектор перпендикулярен , то сила и пара сил (с моментом ) лежат в одной плоскости zOy и приводятся к одной равнодействующей силе равной и параллельной силе и приложенной в точке К, отстоящей от оси на расстояние

 м.

Итак, данная система сил приводится к равнодействующей силе приложенной к точке К и направленной параллельно оси y, причем Н.

Задача 1.28. По трем непересекающимся и непараллельным ребрам прямоугольного параллелепипеда действуют три равные по модулю силы Р (рис.1.29). Какое соотношение должно существовать между ребрами a, b и c, чтобы эта система приводилась к одной равнодействующей?

Ответ: а = 0; b = с.

Задача 1.29. К четырем вершинам A, H, B и D куба приложены четыре равные по модулю силы: Р₁ = Р₂ = = Р₃ = Р₄ = Р, причем сила Р₁ направлена по АС, Р₂ – по HF, Р₃ – по BE и Р₄ – по DG (рис.1.30). Привести эту систему к простейшему виду.

Ответ: равнодействующая , приложенная в точке В под углом 45 к осям x и z.

Задача 1.30. Три силы Р₁, Р₂ и Р₃ лежат в координатных плоскостях и параллельны осям координат, но могут быть направлены как в ту, так и в другую сторону (рис.1.31). Точки их приложения А, В и С находятся на заданных расстояниях a, b и с от начала координат. Какому условию должны удовлетворять эти силы, чтобы они приводились к одной равнодействующей? Какому условию должны удовлетворять величины этих сил, чтобы существовала центральная винтовая ось, проходящая через начало координат?

Ответ:

З адача 1.31. К правильному тетраэдру ABCD с ребрами, равными а, приложена сила F₁ по ребру АВ и сила F₂ по ребру CD (рис.1.32). Найти координаты x и y точки пересечения центральной винтовой оси с плоскостью Оxy.

Ответ:

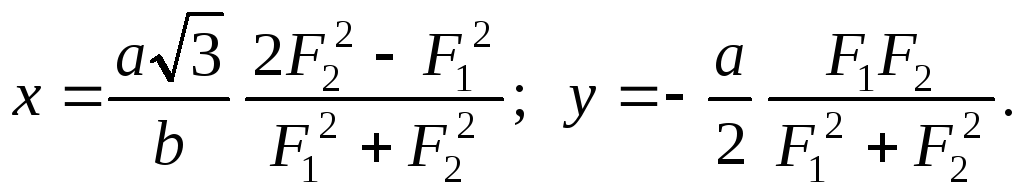
Задача 1.32. По ребрам куба, равным а, действуют двенадцать равных по модулю сил Р (рис.1.33). Привести эту систему сил к каноническому виду и определить координаты x и y точки пересечения центральной винтовой оси с плоскостью Оxy.

Ответ:

Задача 1.33. По ребрам прямоугольного параллелепипеда, соответственно равным 10, 4 и 5 м, действуют шесть сил: Р₁ = 4 Н, Р₂ = 6 Н, Р₃ = 3 Н, Р₄ = 2 Н, Р₅ = 6 Н, Р₆ = 8 Н (рис.1.34). Привести эту систему сил к каноническому виду и определить координаты x и y точки пересечения центральной винтовой оси с плоскостью Oxy.

Ответ: F = 5,4 Н; M_О = –47,3 Нм; cos = 0; cos = 0,37; cos = 0,93; x = –11,9 м; y = –10 м.