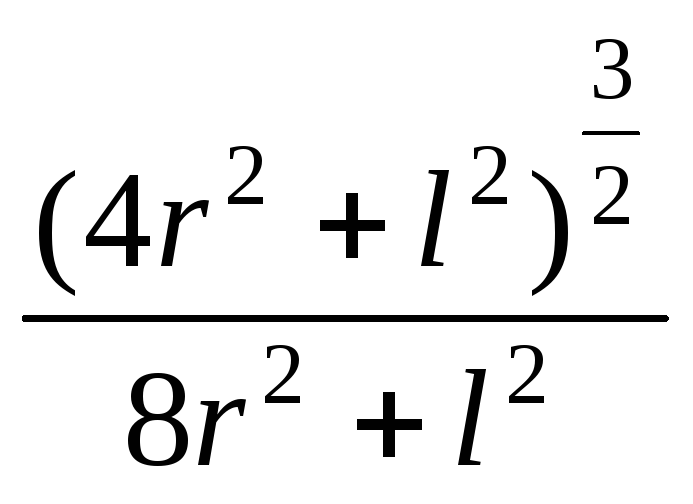2.2. Скорость и ускорение точки

Основными кинематическими характеристиками движения точки являются скорость и ускорение.

Скорость точки характеризует быстроту изменения положения точки. Вектор скорости точки выражается производной от радиуса-вектора r , определяющего ее положение, по времени:

.

Проекции скорости на оси декартовых координат равны производным соответствующих координат по времени:

; ; .

Модуль скорости

.

Направление вектора скорости определяется направляющими косинусами

; ; .

Если уравнение задано в естественной форме, то скорость точки

,

где – орт касательной, направленный в сторону увеличения дуговой координаты s; v_ – алгебраическая величина скорости, .

Ускорение характеризует изменение скорости с течением времени по модулю и направлению. Ускорение точки выражается производной от скорости по времени или второй производной от радиуса-вектора точки по времени

.

Проекции ускорения на оси неподвижной декартовой системы координат следующие:

.

Модуль ускорения

.

Направление вектора ускорения определяется направляющими косинусами (аналогично направлению вектора скорости).

В случае, когда движение описывается естественным способом, ускорение определяется через проекции на естественные оси координат. Ограничиваясь плоским случаем, в дополнение к только что введенному орту касательной введем орт главной нормали , направленный в сторону вогнутости траектории. При переходе от одной точки траектории к другой естественные оси, оставаясь между собой ортогональными, непрерывно поворачиваются.

Ускорение точки определяется как векторная сумма касательного и нормального ускорений точки:

.

Касательное ускорение характеризует изменение скорости по величине (по модулю): . Оно равно нулю, когда величина скорости при движении остается неизменной.

Нормальное ускорение описывает изменение скорости по направлению:

,

где  – радиус кривизны траектории.

При прямолинейном движении точки w_n = 0, так как радиус кривизны прямой равен бесконечности.

Модуль полного ускорения

.

Пример 2.2. Линейка эллипсографа АВ = l скользит концом А по оси абсцисс и концом В по оси ординат (рис.2.6). Линейка приводится в движение кривошипом ОС = 0,5l, шарнирно прикрепленным к ее середине. Расстояния АМ = а и ВМ = b известны. Угол  между осью абсцисс и кривошипом изменяется пропорционально времени:  = kt.

Найти уравнение движения точки М эллипсографа и уравнение ее траектории. Определить радиус кривизны траектории точки М, ее скорость, касательное, нормальное и полное ускорения при произвольном положении механизма и, в частности, в моменты времени t₁ = 0 и t₂ = /(2k).

Решение. Для составления уравнений движения точки М спроектируем отрезки ВМ и АМ на оси абсцисс и ординат соответственно. Треугольник ОАС равнобедренный: ОС = АС = 0,5l. Следовательно, СОА = САО =   = kt. Тогда координаты точки М следующие:

x = BM cos  = b cos kt;

y = AM sin  = a sin kt.

Этими равенствами определяется закон движения точки М.

Для определения траектории представим уравнение движения точки в виде

возведем эти равенства в квадрат и сложим их:

Таким образом, траектория точки М – эллипс с полуосями b и a (рис.2.7).

Для определения скорости точки М вычислим первые производные от координат по времени, равные проекциям скорости точки на соответствующие оси координат:

Тогда скорость точки М

Проекции ускорения на оси координат находим, вычисляя первые производные по времени от проекций скоростей или вторые производные по времени от координат точки:

или, с учетом уравнений движения точки,

Модуль полного ускорения

Следовательно, ускорение точки М направлено по радиусу-вектору, проведенному из точки М в точку О, и по величине прямо пропорционально расстоянию точки М от начала координат. Проекция ускорения на касательную определяется как производная от проекции скорости на касательную по времени:

.

Но так как , то модуль нормального ускорения

.

Зная модули нормального ускорения точки и скорости, получим радиус кривизны траектории

.

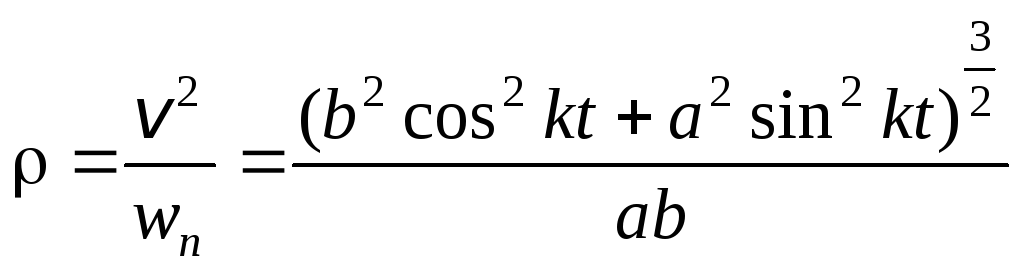Теперь можем вычислить основные кинематические величины для моментов времени t₁ = 0 и t₂ = /2k:

Параметр	x	y	v	w	w	wn	
t1	b	0	ak	–bk2	0	k2b	a2/b
t2	0	a	–bk	–ak2	0	k2a	b2/a

Задача 2.6. Кривошип ОА длиной r вращается равномерно относительно точки О в плоскости чертежа; угол  = kt (рис.2.8). Шатун АВ шарнирно соединен с концом кривошипа в точке А и проходит через неподвижный цилиндрический шарнир N. Длина АВ = l (l > 2r). Записать уравнения движения точки В, проекции ее скорости и ускорения на оси координат, касательного, нормального и полного ускорения, а также радиуса кривизны траектории при произвольном положении механизма. Определить координаты, скорость, ускорение точки В и радиус кривизны ее траектории при  = 0 и  = .

Ответ:

;

;

;

.

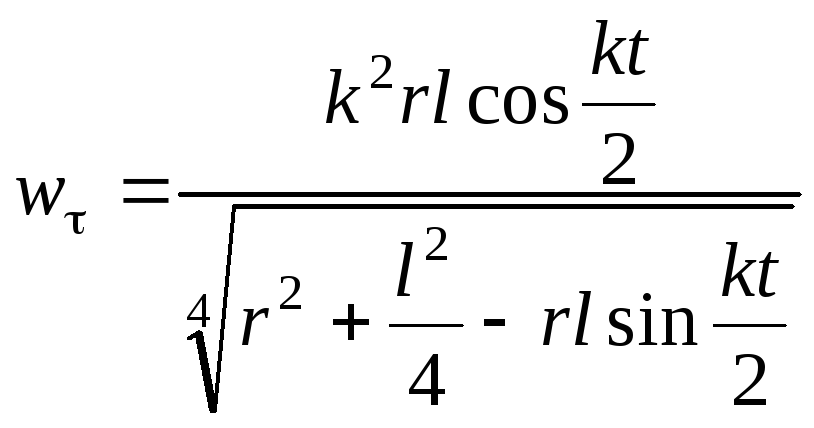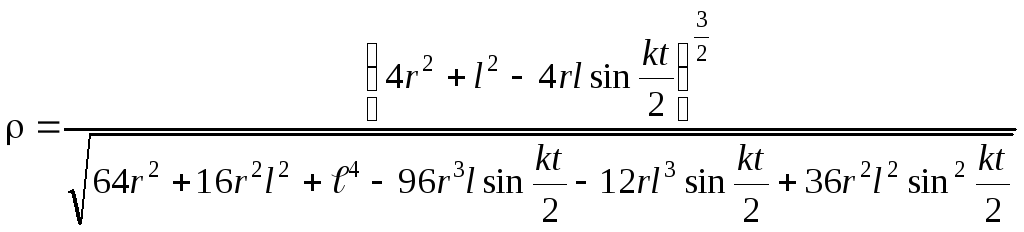Значения параметров движения в моменты времени ₁ = 0 и ₂ =  следующие:

Параметр	x	y	v	w	w	wn	
1	r	–l
2	–r + l	0			0

Задача 2.7. Груз С (рис.2.9) поднимается по вертикальной направляющей при помощи троса, перекинутого через неподвижный блок А, отстоящий от направляющей на расстояние АО = а. Вычислить скорость и ускорение груза С в зависимости от расстояния ОС = х, если свободный конец троса тянут с постоянной скоростью u.

Ответ: ; .

Задача 2.8. Даны уравнения движения точки: x = 4 + 6t², y = 3t² – 1 (x и y – в метрах, t – в секундах). Определить траекторию, скорость и ускорение точки.

Ответ: ; м/с; м/с².

Задача 2.9. Движение точки задано уравнениями x = 2t; y = e^–4t sin4t. Записать уравнение траектории; найти моменты времени, в которые вектор скорости точки параллелен оси Ох, и моменты времени, в которые вектор скорости точки пересекает ось Ох.

Ответ: y = e^–2x sin2x(0  x < ); , ; , .

Задача 2.10. По уравнениям движения точки x = t² / 2 и y = t³ / 3 (x и y – в метрах, t – в секундах) определить моменты времени, в которые угол между векторами скорости и ускорения точки .

Ответ: t₁ = 1 c, t₂ = 0,5 c.

Задача 2.11. В грохоте (рис.2.10), служащем для сортировки руды, кривошип О₁А вращается равномерно вокруг оси О₁ с частотой 60 мин^–1. Посредством вилки АВ он передает вращение кривошипу О₂В, вращающемуся вокруг оси О₂. Известно, что О₁А = О₂В = АВ = = 10 см; О₁О₂ = 4 см. Найти линейную скорость точки В для трех положений механизма: 1) когда точка А занимает положение на продолженной влево линии центров О₁О₂; 2) когда вилка АВ параллельна линии центров О₁О₂; 3) когда точка В находится на продолженной направо линии центров.

Ответ: 1) v₁ = 4,5 м/c; 2) v₂ = 6,28 м/c; 3) v₃ = 8,8 м/c.