
978-966-10-2413-6_Matematuka 11_rus
.pdf
Исследование функций и построение их графиков с помощью производной |
191 |
|
|||||||||
|
|
|
Итог |
|
|
|
|
|
|
|
|
|
|
Основные понятия |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
|
Определение |
|
|
Иллюстрация |
|
|
|||||
|
Точка х0 |
называется точкой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
максимума функции у |
= f (x), |
|
|
|
|
|
|
|
|
|
|
если для всех х ≠ х0 из некоторой |
|
|
|
|
|
|
|
|
||
|
окрестности этой точки выпол- |
|
|
|
|
|
|
|
|
||
|
няется неравенство f(x) < f(х0). |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
|
Точка х0 называется точкой ми- |
|
|
|
|
|
|
|
|
||
|
нимума функции у = f(x), если для |
|
|
|
|
|
|
|
|
||
|
всех х ≠ х0 |
из некоторой окрест- |
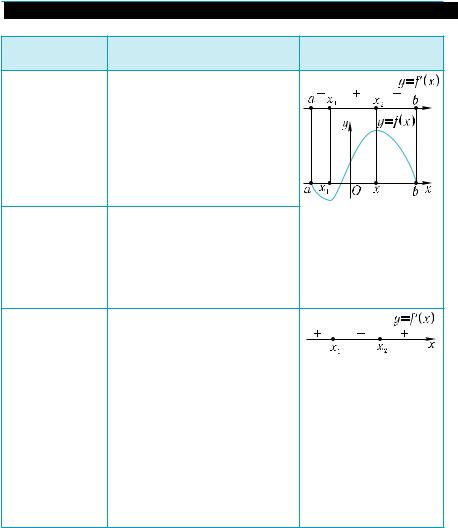
Точка х1 — точка мини- |
|
|||||||
|
ности этой точки выполняется |
|
|||||||||
|
мума функции у = f(х). |
|
|
||||||||
|
неравенство f(x) > f(х0). |
|
|
|
|||||||
|
|
Точка х2 — точка макси- |
|
||||||||
|
|
|
|
мума функции |
у = f(х). |
|
|
||||
|
Пусть функция у = f(x) определена на |
f(b) — наименьшее значе- |
|
||||||||
|
некотором промежутке и х0 |
— точка |
ние функции на [a; b]. |
|
|
||||||
|
из этого промежутка. |
|
f(x0) — наибольшее значе- |
|
|||||||
|
Значение функции у = f(х) в точке |
ние функции на [a; b]. |
|
|
|||||||
|
х0 называют наибольшим значе- |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
|
нием функции на промежутке, |
|
|
|
|
|
|
|
|
||
|
если оно не меньше любого друго- |
|
|
|
|
|
|
|
|
||
|
го значения функции на нем. |
|
|
|
|
|
|
|
|
||
|
Значение функции у = f(х) в точке |
|
|
|
|
|
|
|
|
||
|
х0 называют наименьшим значе- |
|
|
|
|
|
|
|
|
||
|
нием функции на промежутке, |
|
|
|
|
|
|
|
|
||
|
если оно не больше любого друго- |
|
|
|
|
|
|
|
|
||
|
го значения функции на нем. |
|
|
|
|
|
|
|
|
||
192 |
|
|
Раздел 3. Производная и ее приложения |
|||
|
Основные утверждения |
|||||
Название |
Формулировка |
Иллюстрация |
||||
теоремы |
||||||
|
|
|
|
|
||
Признак |
Если на некотором ин |
|
||||
монотонности |
тервале |
|
производная |
|
||
функции |
положительна, то фун |
|
||||
|
кция возрастает на этом |
|
||||
|
интервале, а если про |
|
||||
|
изводная отрицательна, |
|
||||
|
то функция убывает на |
|
||||
Признак |
этом интервале. |
|
|
|||
Если на некотором ин |
|
|||||
постоянства |
тервале |
|
производная |
|
||
функции |
функции |
|
тождественно |
|
||
|
равна нулю, то функция |
|
||||
|
постоянна на этом ин |
|
||||
|
тервале. |
|
|
|
|
|
Достаточное |
Пусть f ′(х0) = 0. |
|
|
|||
условие |
1. Если f |
′(x) > 0 на неко |
|
|||
экстремума |
тором интервале (а; х0) и |
Точка х1 — точка |
||||
дифференци- |
f′(x) < 0 на некотором ин |
|||||
руемой |
тервале (х0; b), то точка |
максимума функции |
||||
функции |
х0 является точкой мак |
у = f(х). |
||||
|
симума функции. |
|
Точка х2 — точка |
|||
|
2. Если f |
′(x) < 0 на неко |
минимума функции |
|||
|
тором интервале |
(а; х0) |
у = f(х). |
|||
|
и f ′(x) > 0 на некотором |
|
||||
|
интервале |
(х0; b), то точ |
|
|||
|
ка х0 является точкой |
|
||||
|
минимума функции. |
|
||||
Готовимся к тематичес кому оцениванию по теме « Производная и ее приложения»
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задания для самоконтроля |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
?? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
1°. |
На рисунке изображены графики законов |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
прямолинейного движения точек: а) |
x = x1(t), |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
б) x = x2(t).Двигались ли точки равномерно? |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
Если равномерно, то с какими скоростями? |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
2°. |
Какая из следующих величин меняется рав- |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
номерно в зависимости от переменной t: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
а) v = |
5t |
; |
|
|
б) |
s = |
5 |
; |
|
в) m = |
5t2 |
? |
|
|
|
|
|
|
||||||||
3. |
|
2 |
|
|
|
2t |
|
2 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
На рисунке изображен график закона прямолинейного дви- |
|||||||||||||||||||||||||||
|
|
жения точки. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
а°) В какой момент времени: t1 = 1 c или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
t2 = 4 c — точка имела большую скорость? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
б°) В какие моменты времени скорость |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
точки равнялась 0? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
в) Сравните среднюю скорость точки на |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
промежутке [0; 5] и мгновенную скорость |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
при t = |
4 с. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4°. |
Чему равен угловой коэффициент каса- |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
тельной к графику функции у = |
x |
в точке с абсциссой х = 4? |
||||||||||||||||||||||||
5°. |
Какой угол (тупой или острый) образует с осью х касательная |
|||||||||||||||||||||||||||
|
|
к графику функции у = х2 |
– 3 в точке с абсциссой х = |
–2? |
||||||||||||||||||||||||
6. |
|
Запишите |
уравнение |
касательной к графику |
|
функции |
||||||||||||||||||||||
у = 2sin x в точке с абсциссой х = 0.
194 |
Раздел 3. Производная и ее приложения |
||||||
|
|
|
|
|
|
|
|
7. |
Существует ли точка на графике функции y = |
1 |
такая, что |
||||
|
|
|
|
x |
|
|
|
|
|
касательная к нему в этой точке параллельна: а) оси х; б) пря- |
|||||
|
|
мой у = х; в) прямой у = –х? |
|
|
|
|
|
8°. |
В какой из приведенных точек производ- |
|
|
|
|
||
|
|
|
|
||||
|
|
ная функции у = f(x), график которой изо- |
|
|
|
|
|
|
|
бражен на рисунке, отрицательна? |
|
|
|
|
|
|
|
|
|
|
|
|
|
9°. |
Сравните скорости изменения функции у = ln x в точках х1 = 2 |
||||
|
и х2 = 3. |
|
|
|
|
10°.На рисунке изображен график фун- |
|
|
|||
|
кции, определенной на отрезке [–3; 5]. |
|
|
||
|
Укажите: |
|
|
|
|
|
а) точки, где производная функции |
|
|
||
|
равна нулю; |
|
|
|
|
|
б) точки экстремума функции; |
|
|
|
|
|
в) промежутки, на которых производ- |
|
|
||
|
ная функции положительна; |
|
|
|
|
|
г) наибольшее и наименьшее значения функции в области оп- |
||||
|
ределения. |
|
|
|
|
11. |
Какая из следующих функций возрастает на всей числовой оси: |
||||
|
а) y = ex − x; |
б) y = 2 + sin x; |
|||
|
в) y = x3 + 2x + 1; |
г) y = |
x |
1 |
? |
|
|
|
2 + 1 |
|
|
12.На рисунке изображены графики производных функций y = f (x), y = g(x), y = ϕ(x) . Какая из этих функций возрастает?
13.Известно, что f ′(x) = (x + 1)2(x – 2). Укажите:
а) промежутки возрастания и убывания функции у = f(x); б) точки экстремума функции у = f(x).
Готовимся к тематическому |
оцениванию по теме |
195 |
14.На рисунке изображен график произ-  водной функции у = f(x), заданной на
водной функции у = f(x), заданной на
промежутке [–3; 4]. Укажите:
а) промежутки возрастания и убывания 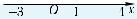 функции у = f(x);
функции у = f(x);  б) точки экстремума функции у = f(x).
б) точки экстремума функции у = f(x).  Среди функций, графики которых изо- бражены на рисунке, выберите ту, которая своё наименьшее
Среди функций, графики которых изо- бражены на рисунке, выберите ту, которая своё наименьшее
значение принимает в точке минимума, а наибольшее — на одном из концов области определения.
16°.Известно, чтоf′(x) = –3 при каждомх. В какой точке промежутка [–2; 1] функцияу = f(x) принимает наибольшее значение?
17°.Известно, что f ′(x) = x(x + 2)(x – 2). В каких точках следует вы- числить значения функции у = f(x), чтобы найти ее наиболь- шее и наименьшее значения на промежутке [–1; 3]?
18°.Пусть x = 2t3 − 6t — закон прямолинейного движения точки. Укажите наименьшую и наибольшую координаты точки на промежутке времени [0; 2].
19. Какой из графиков, приведенных на рисунке, может быть графиком функции y = f(x), если f ′(x) = 3х – 1?
20. Производная функции у = f(x) изобра-
жена на рисунке. Укажите наимень-  шее значение функции у = f(x) на про-
шее значение функции у = f(x) на про-  межутке [–1; 1].
межутке [–1; 1].  21. Какое из следующих утверждений яв-
21. Какое из следующих утверждений яв-  ляется неверным?
ляется неверным?  а) Наименьшее значение функция может принимать не толь-
а) Наименьшее значение функция может принимать не толь-
ко в точке минимума.
196 Раздел 3. Производная и ее приложения
б) Наибольшее и наименьшее значения функция может при- нимать только в своих точках экстремума.
в) Существует функция, у которой совпадают ее наибольшее и наименьшее значения.
22*.На рисунке справа изображен график фун-  кции y = f(x). На каком из рисунков ниже изо-
кции y = f(x). На каком из рисунков ниже изо-  бражен график производной этой функции?
бражен график производной этой функции? 
Ответы к заданиям для самоконтроля
1. Обе точки движутся равномерно. v1(t) = − |
2 |
, v2(t) = |
3 . 2. a). 3. a) t1 = 4 с; |
||||
|
|
|
1 |
|
3 |
|
|
б) t = 5; в) v(4) > v |
|
[0; 5]. 4. |
. 5. Тупой. 6. у = 2х. 7. а) Нет; б) нет; в) в точках |
||||
|
ср |
|
4 |
|
|
|
|
с координатами (1; 1) и (–1; –1). 8. х2. 9. v(2) > v(3). 10. а)х1 = –1;х2 = 3; б)х1 = –1;
х2 = 2; х3 = 3; в) (–1; 2) (3; 5); г) наибольшее значение функции равно 4, наи- меньшее равно –1. 11. в). 12. у = f(x). 13. а) Функция убывает на промежутке
(–∞; 2] и возрастает на промежутке [2; +∞); б) х = 2. 14. а) Функция убывает на каждом из промежутков [–3; –2], [3; 4] и возрастает на промежутке [–2; 3];
б)х1 = –2; х2 = 3. 15. у = h(x). 16. х = –2. 17. х1 = –1; х2 =0; х3 =2; х4 = 3. 18. –4; 4.
19. в). 20. f(–1). 21. Неверным является утверждение б). 22. а).
Образец контрольной работы № 3
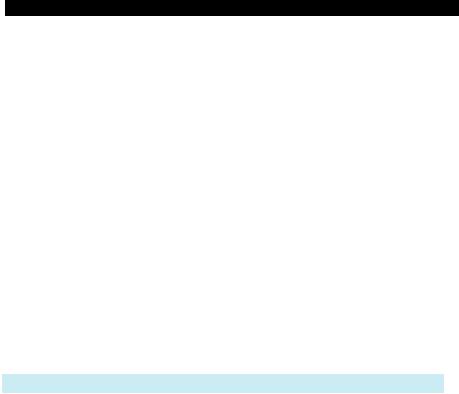
1.На рисунке изображен график
функции y = f(x), определенной на  промежутке [–2; 7]. Найдите:
промежутке [–2; 7]. Найдите:
1°) в какой из точек: х1 = 1 или х2 =  = 2 — функция имеет большую ско-
= 2 — функция имеет большую ско-  рость изменения; 2°) точки экстремума функции;
рость изменения; 2°) точки экстремума функции;
3°) промежутки, где производная функции отрицательна; 4°) наибольшее и наименьшее значения функции y = f(x) на промежутке [0; 7];
5) точки, в которых функция y = f(x) недифференцируема; 6) знак числа (f ′(1) – f ′(2)) f ′(3).
Готовимся к тематическому |
оцениванию по теме |
197 |
2.Дана функция у = х4 – 2х2 – 3. Найдите:
1°) угловой коэффициент касательной к графику функции в точке с абсциссой х = 12 ; 2°) промежутки возрастания и убывания функции и ее точки экстремума;
3°) наибольшее и наименьшее значения функции на проме-
жутке [0; 2]; 4) уравнение касательной к графику функции в точке пересе-
чения графика с осью ординат.
Материальная точка движется прямолинейно по закону
2sin t + 1.
|
1°) Какова скорость точки в момент времени t = |
p ? |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
2) Укажите все моменты времени, в которые точка меняет на- |
|||||||||||
|
правление движения. |
|
|
|
|
|
||||||
|
3*) Найдите ускорение точки в те моменты времени, когда |
|||||||||||
|
она меняет направление движения. |
|
|
|
|
|||||||
|
|
|
|
Физический смысл производной |
Таблица 27 |
|||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Обозначение |
|
Содержание |
|
|||||
Df(х0) = f(х0 + Dх) – f(х0) |
|
приращение функции |
||||||||||
|
|
|
|
|
|
|
|
|
у = f(x) в точке |
х0, со- |
||
|
|
|
|
|
|
|
|
|
ответствующее |
прира- |
||
|
|
|
|
|
|
|
|
|
щению аргумента Dх |
|
||
|
f (x0 + |
x) − f (x0 ) |
= |
f (x0 ) |
|
средняя скорость изме- |
||||||
|
|
нения функции на про- |
||||||||||
|
|
|
|
x |
|
|||||||
|
|
|
x |
|
|
|
|
межутке [x0; x0 + Dх] |
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
lim |
f (x0 ) |
= lim |
f (x0 |
+ x) − f (x0 ) |
= f (x0 ) |
скорость |
изменения |
||||
|
|
|
|
|
|
функции |
в точке x , |
|||||
|
x →0 |
|
x |
x →0 |
|
|
x |
′ |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
или производная фун- |
|||
|
|
|
|
|
|
|
|
|
кции в точке x0 |
|
|
|

198 |
|
Раздел 3. Производная и ее приложения |
||
|
Геометрический смысл производной |
|||
|
|
|
Таблица 28 |
|
Обозначение |
Содержание |
Геометрическая |
||
интерпретация |
||||
|
|
приращение |
||
М0Р = Dх |
|
|
||
|
|
аргумента |
|
|
МР = Df(х0) |
|
приращение функ- |
||
|
|
ции в точке х0 |
|
|
l |
|
касательная |
|
|
|
|
к графику функции |
||
tg a = f ′(х0) |
|
в точке М0 |
|
|
|
угловой коэффици |
|||
|
|
ент касательной l |
||
у = f(х ) + |
|
уравнение каса- |
|
|
+ f ′(x0 ) (х – х ) |
тельной к графику |
|||
0 |
0 |
функции в точке |
М0 |
|
Правила дифференцирования функции
Таблица 29
|
|
|
|
|
′ |
′ |
|
′ |
|
′ |
′ |
|
( f (x) + g(x)) |
= f (x) |
+ g (x), |
(cf (x)) |
= cf (x), |
||||||
|
( f (x) g(x)) = f (x)g(x) + g (x)f (x), |
|
|||||||||
|
|
|
|
|
′ |
′ |
|
′ |
|
|
|
|
|
|
′ |
|
′ |
|
|
′ |
|
|
|
|
f (x) |
= |
f (x)g(x) − f (x)g (x) |
, |
|
||||||
|
|
|
|
|
g |
2 |
(x) |
|
|
||
|
g(x) |
|
|
|
|
|
|
||||
( |
|
f(kx + b))′ = kf ′(u), где и = kx + b. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|

Готовимся к тематическому оцениванию по теме |
199 |
|
||
|
Алгоритм нахождения интервалов монотонности и точек |
|||
|
|
экстремума дифференцируемой функции |
||
|
|
|
Таблица 30 |
|
|
№ |
Содержание этапа |
|
|
|
этапа |
|
|
|
|
|
|
|
|
1.Найти точки, в которых производная функции равна нулю.
2.Разбить область определения функции найденными точ- ками на интервалы.
3.Определить знак производной на каждом из полученных интервалов.
Сделать вывод: если на интервале f ′(x) >0, то на этом ин-
4.тервале функция возрастает; если на интервале f ′(x) < 0, то на этом интервале функция убывает.
5.Проверить, меняет ли производная знак в точках, где производная равна нулю.
Если в точке производная изменяет знак с «+» на «–»,
6.то эта точка является точкой максимума, если с «–» на «+», — то точкой минимума.
Алгоритм нахождения наибольшего и наименьшего значений дифференцируемой функции на отрезке
Таблица 31
№ |
Содержание этапа |
|
этапа |
||
|
1.Найти точки, в которых производная функции равна нулю.
2.Отобрать те из найденных точек, которые принадлежат заданному отрезку.
3.Вычислить значения функции в этих точках и на концах отрезка.
Наибольшееизполученныхчиселявляетсянаибольшим
4.значением функции на данном отрезке, наименьшее – наименьшим значением функции на данном отрезке.

|
Исторический комментарий |
Вопросы, относящиеся к дифференциальному исчислению (по- |
|
строение касательных к кривым, нахождение максимумов и ми- |
|
нимумов), эпизодически возникали еще у Евклида, Архимеда и |
|
других древнегреческих математиков и в последующие периоды. |
|
Успехи, достигнутые в XVII ст. наукой, техникой, естествозна- |
|
нием, не могли не повлиять на развитие математики и, в свою |
|
очередь, математика существенно способствовала научному про- |
|
грессу. Ведь законы движения планет, открытые И. Кеплером |
|
(1571–1630) в начале этого века, исследовались математически- |
|
ми методами и формулировались на языке математики. Немно- |
|
го позже Г. Галилей (1564–1642) математически сформулировал |
|
законы падения тел. Эти и многие другие результаты в физике, |
|
создание П. Ферма (1601–1665) и Р. Декартом (1596–1650) коор- |
|
динатного метода привели к введению «движения» в математику, |
|
возникновению математики переменных величин, одним из ос- |
|
новных понятий которой является производная функции. |
|
Можно назвать имена многих ученых XVII ст. (П. Ферма, И. Барроу |
|
(1630–1671), Д. Валлис (1616–1703) и др.), труды которых подготовили |
|
почву для решающего шага, сделанного в конечном итоге И.Ньютоном |
|
(1643–1727) и Г. Лейбницем (1646–1716), которые обобщили накоплен- |
|
ные к этому времени отдельные результаты и факты, превратив их в |
|
целостную теорию дифференциального исчисления. |
|
И. Ньютон сделал свои открытия в 60–70 годы XVII ст., но об- |
|
народовал их значительно позже. Поэтому приоритет открытия |
|
он разделил с Г. Лейбницем, причем благодаря последнему ос- |
|
новные идеи нового исчисления приобрели широкое признание. |
|
Развитие дифференциального исчисления привело к созда- |
|
нию теории функций, одного из важнейших разделов математи- |
|
ки. В сокровищницу этой математической дисциплины весомый |
|
вклад внесли и украинские ученые: М.П. Кравчук (1892–1942), |
|
С.Н. Бернштейн (1880–1968), Н.И. Ахиезер (1901–1980), М.Г. Крейн |
|
(1907–1989), В.К. Дзядык (1919–1998) и многие другие. |
|
