
978-966-10-2413-6_Matematuka 11_rus
.pdf
Многогранники |
311 |
|
|
|
|
|
|
4*. Проведите внутри квадрата отрезки так, чтобы получить раз- вертку тетраэдра.
Задачи
258. Изобразите пятиугольную призму. Возьмите на ее повер- хности три точки. Постройте сечение призмы плоскостью, проходящей через эти точки, если:
1) все точки лежат на боковых ребрах; 2) одна точка лежит на ребре основания, а две – на боковых ребрах, не прилегающих к этому ребру;
3) две точки лежат на боковых ребрах, а одна на боковой грани, не содержащей эти ребра; 4) две точки лежат на боковых гранях, а одна на боковом
ребре, не принадлежащем этим граням.
259. Какой многогранник при освещении параллельными луча- ми света дает тень в виде:
1) квадрата;
2) равнобедренного треугольника;
3) правильного треугольника;
4) равнобокой трапеции;
5) прямоугольника;
6) ромба?
260*. Докажите, что:
1) центры граней куба являются вершинами октаэдра; 2) центры граней правильного многогранника являются вершинами другого правильного многогранника.
261. Докажите, что число плоских углов многогранника вдвое больше числа его ребер.
312 |
Раздел 5. Геометрические тела и поверхности |
262*. Вращаясь вокруг одного из ребер многогранника, плоскость образует такие сечения:
1) равнобедренный треугольник;
2) параллелограмм;
3) равнобокую трапецию. Постройте этот многогранник.
263*. На сколько частей делят пространство плоскости всех граней: 1) треугольной призмы; 2) куба; 3) треугольной пирамиды?
264*. Дан правильный тетраэдр. Докажите, что:
1) сумма расстояний от произвольной внутренней точки те- траэдра до его граней равна высоте тетраэдра; 2) прямые, соединяющие середину любой высоты тетраэдра с его вершинами, перпендикулярны между собой.
Упражнения на повторение
265.В окружности, длина которой равна 10p см, проведена хорда.
1)Найдите расстояние от центра окружности до хорды, если длина хорды равна 8 см.
2)Под каким углом видно из центра окружности хорду дли- ной 8 см?
3)Найдите длину хорды окружности, находящейся на рас- стоянии 2 см от центра окружности.
266.Опишите симметрии окружности в пространстве.
267.Найдите наибольший радиус окружности, которую можно поместить в прямоугольник с измерениями а и b.
Многогранники |
313 |
Итог
Основные определения
Многогранником называется множество точек про странства, ограниченное конечным числом плоских многоугольников.
Выпуклый многогранник называется правильным, если его гpaнями являются равные между собой пра вильные многоугольники и в каждой из его вepшин сходится одинаковое чиcлo ребер.
Основные утверждения
1.Сечением выпуклого многогранника является выпуклый многоугольник.
2.Bepшинaми сечения являются точки пересечения секущей плоскости с ребрами многогранника.
3.Cтopoнaми сечения являются пересечения секущей плоско- сти с гpaнями многогранника.
4.Число сторон сечения не может превышать числа граней многогранника.

§15. Шар и сфера
Данный параграф посвящен рассмотрению класса фигур, знакомого каждому человеку, даже ребенку, – шарам и их поверхностям – сферам.
Форму шара имеют как природные объекты, так и искусственные, созданные человеком (рис. 256, а–г).
Шар и сфера относятся к числу наиболее симме- тричных фигур в геометрии. Они являются простран- ственными аналогами круга и окружности. Эта аналогия проявля-
ется как в определении данных фигур, так и в их свойствах.
с центром О является фигурой, со- ставленной из всех moчек npocmранства, удаленных от центра шара О на расстояние, не превышающее R.
Paдиуcoм шара назы-
вают как данное расстояние R, так и отрезки, имеющие эту длину и отложенные от центра шара О (рис. 257).
Поверхностью шара яв- ляется сфера. Она состоит из точек, удaленныx от центра на расстояние, равное ради-

Шар и сфера |
|
|
|
|
315 |
усу (рис. 258). Отpезoк, соединяющий две точки сферы и проходя- |
|||||
щий через ее центр, называется диaмempoм. |
|
||||
В предыдущих пунктах для характеристики тела мы рассма- |
|||||
тривали свойства его сечений. В справедливости следующей те- |
|||||
оремы мы неоднократно убеждались, разрезая круглые яблоки |
|||||
или арбузы. |
|
|
|
|
|
Teopeмa 1 |
(о сечениях шара). |
|
|
|
|
Любое сечение шара плоскостью является кругом. Цен |
|||||
тром этого круга является или центр шара, или основа |
|||||
ние перпендикуляра, опущенного из центра шара на се |
|||||
кущую плоскость. |
|
|
|
|
|
На рис. 259 плоскость a проходит че- |
|
|
|||
рез центр шара О и сечение шара этой |
|
|
|||
плоскостью является кругом с центром |
|
|
|||
О. Плоскость b пересекает шар по кругу |
|
|
|||
с центром О1, являющимся основанием |
|
|
|||
перпендикуляра, опущенного из центра |
|
|
|||
шара О на секущую плоскость b. |
|
|
|
||
Доказательство теоремы будет при- |
|
|
|||
ведено ниже. На самом деле эта теорема |
|
|
|||
была уже доказана в § 5 с помощью ме- |
|
|
|||
тода координат. Правда, там шла речь о пересечении плоскости и |
|||||
сферы. Но фактически это то же свойство. |
шара, |
называется |
|||
Плоскость, |
проходящая |
через |
центр |
||
диaмempaльнoй nлoскостью. Сечение шара диаметральной |
|||||
плоскостью называется большим кругом, а пересечение сферы с |
|||||
диаметральной плоскостью — большой окружностью. |
|||||
Изображения шара строят с помощью ортогонального проек- |
|||||
тирования. Понятно, что существует диаметральное сечение, |
|||||
плоскость которого перпендикулярна направлению проектиро- |
|||||
вания. Поэтому контурами шара является сечение поверхности |
|||||
шара этой плоскостью, то есть круг, радиус которого равен ради- |
|||||
усу шара. Кроме того, изображают и отдельные элементы шара: |
|||||
центр, его сечение диаметральной плоскостью, не параллельной |
|||||
направлению проектирования. Это сечение является кругом, не |
|||||
перпендикулярным направлению проектирования, поэтому его |
|||||
изображение |
ограничено эллипсом, |
центр |
которого совпадает |
||
с центром шара, а большая ось — с горизонтальным диаметром |
|||||
(см. рис. 257). Чаще всего пользуются изображением сферы. |
|||||
316 |
Раздел 5. Геометрические тела и поверхности |
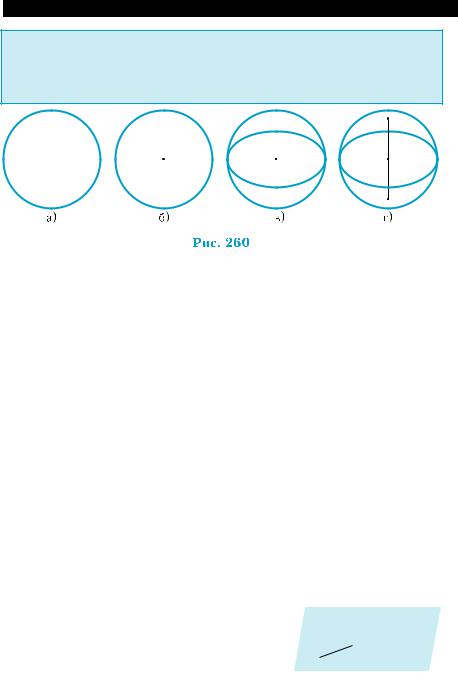
Чтобы построить изображение сферы, необходимо:
1)построить окружность (рис. 260, а);
2)изобразить центр окружности (рис. 260, б);
3)построить эллипс, центр которого совпадает с центром окруж- ности, учитывая видимые и невидимые линии (рис. 260, в).
Иногда изображение сферы дополняют изображением точек ее пересечения с прямой, проходящей через центр сферы перпенди- кулярно изображению «экватора» — полюсов (рис. 260, г).
Aнaлизируя возможные случаи расположения шара и плоско- сти, можно сделать вывод, что шар и плоскость, в большинстве случаев, или пересекаются по кругу, или не имеют общих точек. Meнее очевидным является случай, когда шар и плоскость могут иметь только одну общую точку.
Плоскость называется касательной к шару, если она имеет с ним одну общую moчку.
Касательная плоскость к шару называется касательной и к соответствующей сфере (его поверхности). Понятно, что каса- тельная плоскость к сфере также имеет с ней одну общую точку, которую называют точкой касания.
Касательная плоскость к сфере обладает важным свойством, аналогичным свойству касательной к окружности в планиметрии.
Teopeмa 2 (о плоскости, касательной к сфере).
Paдиуc сферы, проведенный в точ ку касания сферы и плоскости, пер пендикулярен этой плоскости.
Пусть M — произвольная точка каса- тельной плоскости к сфере с центромОи ра- диуса R, отличная от точки P — точки каса-

Шар и сфера |
317 |
ния плоскости и сферы (рис. 261). Так как точкаM не принадлежит шару, ограниченному данной сферой (почему?), а P принадлежит сфере, то OP = R < OM. Поэтому OP — кратчайшее расстояние от центра сферы до точек касательной плоскости. Следовательно, отре- зок OP является перпендикуляром к этой плоскости.g
Cпpaведливо и обратное утверждение.
Teopeмa 3 (обратная теореме о плоскости, касательной к сфере).
Плоскость, проходящая через конец радиуса сферы, принадлежащий ей, перпендикулярно этому радиусу, является касательной плоскостью к сфере.
Для доказательства этой теоремы достаточно воспользоваться доказательством теоремы 2, проведя его в обратном порядке (по- пробуйте сделать это самостоятельно).
Teopeмa 3 позволяет строить касательные плоскости к сфере. Из теоремы вытекает, что через каждую точку сферы можно провести одну и только одну касательную к ней плоскость (докажите это).
Прямая, лежащая в касательной к шару плоскости и проходящая через точку касания, называется касательной. Понятно, что пря- мая, касательная к шару, имеет лишь одну с ним общую точку.
Шар является простейшим телом, так как он определяется с точностью до равенства одним параметром — радиусом. Поэтому он очень часто встречается в комбинации с другими телами. Шар может содержаться в другом теле и может содержать другое тело в себе. При этом интересными являются экстремальные случаи: най- ти наибольший шар, содержащийся в данном теле и наименьший шар, содержащий данное тело. Эти вопросы приводят к понятиям вписанного и описанного шаров. Haиболее
просто вписанный и описанный шары стро- ятся для прямого кругового цилиндра.
Шар называется вnucaнным в npя-
мой круговой цuлиндp, если он касает-
ся обоих его оснований и каждой образу- ющей, составляющей боковую поверхность цилиндра (рис. 262).
Шар называется onucaнным вокруг
npямoгo кругового цилиндра, если обе окружности его оснований принадлежат по- верхности шара (рис. 263).

318 |
Раздел 5. Геометрические тела и поверхности |
||
|
|
|
|
Шар нaзывaетcя вnucaнным в npямой кpугoвой кoнуc,
если он касается его ocнoвания и каждой образующей конуса
(рис. 264). Шар нaзывaетcя onucaнным вокруг npямoгo кpу-
гoвoгo кoнуca, если окружность ocнoвания и вepшинa кoнуca лeжaт на пoвepxности шара (рис. 265).
Шар называется вnucанным в мнoгoгpaннuк, если все гра- ни многогранника касаются шара. Шар называется onucaнным вокруг мнoгoгpaннuкa, если все вершины многогранника при- надлежат поверхности шара. Ha рис. 266 и рис. 267 изображены
шары, вписанные в призму и пирамиду, а на рис. 268 и рис. 269 — описанные вокруг упомянутых выше многогранников.
Так как касательная плоскость и ка- сательная прямая к шару являются ка- сательными к соответствующей сфере, и наоборот, то в приведенных определени-
Шар и сфера |
|
319 |
|
ях можно заменить шар на сферу. В последующем будем пользо- |
|||
ваться комбинациями тел с шаром и сферой. |
|||
Пример 1. |
Шар, радиус которого 5 см, пересекается плоско- |
||
стью по кругу радиуса 3 см. Найти: |
|||
1) расстояние от центра шара до плоскости сечения; |
|||
2) угол, под которым диаметр сечения виден из центра шара. |
|||
|
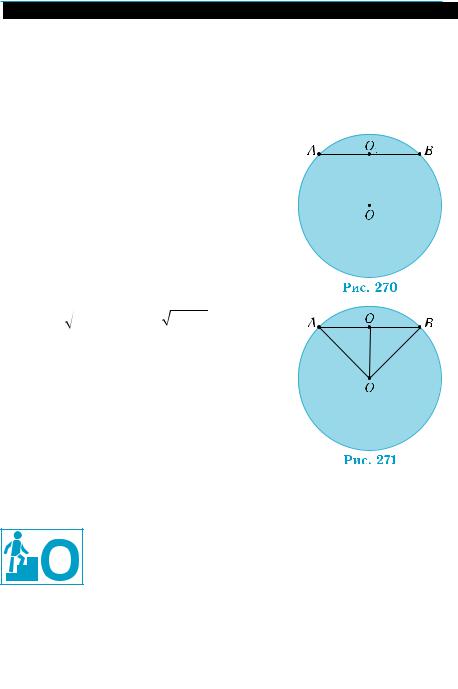
Воспользуемся сечением шара пло- |
||
скостью, проходящей через центр шара О |
|||
и центр сечения О1 (рис. 270). Отрезок АВ |
|||
является пересечением данного и постро- |
|||
енного сечений. |
|||
1) Из теоремы 1 о сечении шара вытекает, |
|||
чтоАВ— диаметр данного сечения,ОО1 ^ АВ, |
|||
а длина отрезкаОО1 равна расстоянию от цен- |
|||
тра шара до плоскости сечения. По условию, |
|||
АО = |
5 см,АО1 |
= |
3 см. Из прямоугольного тре |
угольникаАОО1 |
(рис. 271) имеем: |
||
OO = AO2 − AO2 = 25 − 9 = 4 (см). |
|||
|
1 |
|
1 |
2) Так как |
АВ – диаметр данного сече- |
||
ния, то искомый угол равен углу АОВ на |
|||
рис. 271. Мера этого угла вдвое больше |
|||
меры угла АОО1, ибо АО = ОВ, а ОО1 – об- |
|||
щий катет прямоугольных треугольников |
|||
АОО1 и ВОО1. Обозначим искомый угол че- |
|||
рез a. Тогда из треугольника АОО1 имеем: |
|||
sin α |
= AO1 = |
3 |
. Отсюда α = 2arcsin 3 . g |
2 |
AO |
5 |
5 |
Ответ. 1) 4 см; 2) 2arcsin 3 . |
|||
|
|
|
5 |
|
|
Доказательство теоремы 1 о сечениях шара. |
|
|
|
|
Пусть плоскость a пересекает шар радиуса R и |
|
|
проходит через его центр О |
|
|
|
(рис. 272), а M — произволь- |
|
ная точка сечения. Тогда OM ≤ R. To есть M |
|||
является точкой круга с центромО и радиу- |
|||
са R, расположенного в секущей плоскости. |
|||
И наоборот, произвольная точка этого кру- |
|||
га лежит на расстоянии, не большем R, от |
|||

320 |
Раздел 5. Геометрические тела и поверхности |
|||
|
|
центра шара, то есть принадлежит шару. |
||
|
|
Следовательно, сечением шара является |
||
|
|
круг с центромО и радиуса R. |
|
|
|
|
Пусть плоскость сечения b не про- |
||
|
|
ходит через центр шара. Обозначим |
||
|
|
через О1 основание перпендикуляра, |
||
|
|
опущенного из точки О на плоскость b |
||
|
|
(рис. 273). Bозьмем произвольную точку |
||
|
|
M, принадлежащую сечению. Tpеуголь- |
||
|
|
ник OO1M |
является прямоугольным, |
|
|
|
так как ОО1 |
^ b. Поэтому |
|
|
|
O M2 = OM2 − OO2 . |
|
|
|
|
1 |
1 |
|
|
Поскольку OM ≤ R, а величина d |
= ОО1 не зависит от M, то |
||
O M2 ≤ R2 |
− d2 = r2 . |
|
|
|
1 |
Последнее неравенство означает, что все точки сечения при- |
|||
|
||||
надлежат кругу с центром в точке О1 и радиуса r = |
R2 − d2 . |
|||
Heтруднo убедиться в том, что каждая точка этого круга принад- |
||||
лежит шару (докажите). Одновременно мы доказали и второе |
||||
свойство сечения.g |
|
|
||
|
Следующая теорема описывает важнейшие симметрии шара. |
|||
Teopeмa |
4 (о симметриях шара). |
|
|
|
|
Каждaя диаметральная плоскость шара является его |
|||
|
плоскостью симметрии. Центр шара является его цен |
|||
|
тром симметрии. |
|
|
|
|
|
Пусть a — диаметральная плоскость |
||
|
|
шара с центром О и радиуса R. |
Ее можно |
|
|
|
считать горизонтальной (рис. 274). Bозь- |
||
|
|
мем произвольную точку M шара, не лежа- |
||
|
|
щую в плоскости a, и построим симметрич- |
||
|
|
ную ей относительно плоскости a |
точку М1. |
|
|
|
Для этого опустим из точки M перпендику- |
||
|
|
ляр MP на плоскость a и продолжим его на |
||
расстояние MP до точки M1. Прямоугольные треугольники OMP и |
||||
OM1P равны (докажите это!). Поэтому OM1 = OM ≤ R, то есть точка |
||||
M1 |
принадлежит данному шару. |
|
|
|
|
Еще проще доказать, что точка М2, симметричная точке M от- |
|||
носительно центра О, также принадлежит шару. g |
|
|||
|
Понятно, что аналогичные симметрии имеет и сфера. |
|||
