
978-966-10-2413-6_Matematuka 11_rus
.pdf
Призмы и цилиндры |
301 |
2)величина двугранного угла между смежными боковыми гранями правильной призмы равна величине угла между смежными ребрами основания;
3)сечение призмы, перпендикулярное боковому ребру, пер- пендикулярно и плоскостям всех боковых граней;
4)площадь сечения прямой призмы плоскостью, пересекаю- щей все боковые ребра, не меньше площади основания.
249.Диагональ осевого сечения прямого кругового цилиндра равна 20 см и наклонена под углом 60° к плоскости основа- ния цилиндра. Найдите:
1°) радиус основания цилиндра; 2°) высоту цилиндра;
3°) площадь осевого сечения цилиндра;
4)площадь сечения, проходящего параллельно оси цилин- дра на расстоянии 3 см от нее;
5)площадь сечения цилиндра, проходящего через образую- щую боковой поверхности цилиндра под углом 30° к осевому сечению;
6)угол наклона к плоскости основания цилиндра отрезка, соединяющего центр одного основания с точкой окружности другого.
250.Осевым сечением прямого кругового цилиндра является
квадрат с диагональю 10 2 см. Найдите: 1)° радиус основания цилиндра;
2)° сторону основания правильной треугольной призмы, бо- ковые ребра которой совпадают с образующими цилиндра; 3)° площадь сечения этой призмы плоскостью, проходящей через сторону основания и центр второго основания; 4)° угол наклона плоскости этого сечения к оси цилиндра;
5)площадь сечения цилиндра плоскостью, проходящей па- раллельно его оси на расстоянии 2 см от нее;
6)расстояние от оси цилиндра до параллельного ей сечения цилиндра, площадь которого равна площади основания.
251.Высота прямого кругового цилиндра равна H, радиус осно- вания равен R. Найдите:
1°) площадь осевого сечения; 2°) угол, под которым диаметр верхнего основания виден из центра нижнего;
302Раздел 5. Геометрические тела и поверхности
3)угол, под которым диаметр верхнего основания виден из наиболее удаленной от него точки нижнего основания; 4*) наибольшую длину отрезка, полностью помещающегося в цилиндре.
Радиус основания прямого кругового цилиндра равен 26 см, длина образующей равна 48 см. На каком расстоянии от оси цилиндра следует провести сечение, параллельное оси ци- линдра, чтобы оно имело форму квадрата?
Через образующую прямого кругового цилиндра проходит два сечения. Одно из них — осевое и имеет площадь, в два раза большую площади другого сечения. Найдите угол меж- ду секущими плоскостями.
В прямом круговом цилиндре параллельно его оси на рас- стоянии а от нее проведена плоскость, отсекающая от окруж- ности основания дугу в a радиан. Площадь сечения равна S. Найдите высоту цилиндра.
Площадь прямоугольника равна S. Найдите площадь осево- го сечения прямого кругового цилиндра, свернутого из пря- моугольника.
Упражнения для повторения
256.Дан правильный шестиугольник. Для произвольной его диагонали укажите диагонали: 1) равные ей; 2) перпенди- кулярные ей; 3) параллельные ей.
257.Заполните таблицу.
Фигура |
|
Призма |
|
|
Пирамида |
|
Количество |
4-уголь 5-уголь п-уголь |
4-уголь 5-уголь п-уголь |
||||
ная |
ная |
ная |
ная |
ная |
ная |
|
Граней |
|
|
|
|
|
|
Вершин |
|
|
|
|
|
|
Ребер |
|
|
|
|
|
|

Призмы и цилиндры |
303 |
Итог
Цилиндром нaзывaетcя гeoмeтpическая фигуpa, обра зованная равными и пapaллeльными между coбoй от резками, проведенными изо всех тoчек дaннoй плocкoй фигуры по одну сторону от плоскости этой фигуры.
Призма является цилиндром, в основании которого лeжит многоугольник.
Параллелепипеды

304 |
Раздел 5. Геометрические тела и поверхности |
Основные утверждения
1.Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам. Эта точка являет- ся центром симметрии параллелепипеда.
2.В прямоугольном параллелепипеде квадрат длины любой диагонали равен сумме квадратов трех его измерений.

§14. Многогранники
В этом параграфе рассматривается класс пространственных фигур, к которому принадлежат пирамиды и призмы. Характеристическим свойст-
класса является строение их поверхностей.
Многогранники являются одним из важнейших видов пространственных геометрических фигур.
своему строению они являются пространствен- ными аналогами многоугольников на плоскости. Поверхности многогранников состоят из многоугольников, подобно тому, как границы многоугольников — из отрезков. Именно это свойство многогранников определяет их роль в моделировании простран- ственных форм объектов окружающей среды, в частности тех, ко- торые человек широко использует в своей жизни (рис. 243, а–в).
Пирамиды и призмы являются наиболее применимыми мно- гогранниками. Их объединяет то, что каждая из этих фигур явля- ется множеством точек пространства, ограниченным многоуголь- никами — их гранями.
Многогранником называется множество точек про странства, ограниченное конечным количеством пло ских многоугольников.
Сами эти многоугольники образуют поверхность многогран- ника и называются его гранями, стороны граней называются ре- брами, а вершины — вершинами многогранника.

306 |
Раздел 5. Геометрические тела и поверхности |
На рис. 244 изображены многогранники. Нетрудно увидеть, что они составлены из призм и пирамид. Приведенные примеры показывают, что, пользуясь простыми многогранниками, можно образовать довольно сложные фигуры.
Как и многоугольники, многогранники могут быть выпу- |
|
клыми и невыпуклыми. B выпуклом многограннике две его |
|
произвольные точки можно соединить отрезком, принадлежа- |
|
щим многограннику. Невыпуклый многогранник этим свойст- |
|
вом не обладает. Напpимер, многогранник, изображенный на |
|
рис. 244, в), является невыпуклым, так как отрезок, соединяющий |
|
две ближайшие нecмежные вершины, не принадлежит много |
|
граннику. Многогранник, изображенный на рис. 244, б), является |
|
выпуклым (попробуйте это обосновать). |
|
Далее ограничимся рассмотрением выпуклых многогранни- |
|
ков. Аналогичная договоренность использовалась при изучении |
|
многоугольников в планиметрии. |
|
Изготовленные из картона модели по |
|
верхностей |
многогранников можно разре- |
зать вдоль отдельных ребер и развернуть |
|
так, чтобы они превратились в объединение |
|
многоугольников. Эту фигуру называют |
|
разверткой поверхности многогран-
ника. У поверхности многогранника может быть несколько раз- личных разверток. Taк, на рис. 245, а), б) изображены развертки поверхности одного и того же куба (попробуйте из них склеить куб).
Многогранники относятся к геометрическим фигурам, которые называют телами. Наглядно геометрическое тело можно пред- ставить себе как часть пространства, занятую физическим телом и ограниченную поверхностью.

Многогранники |
307 |
Многогранники часто используются при моделировании окру- жающей среды. В частности, это касается правильных многогран- ников.
Выпуклый многогранник называется правильным, если его гранями являются равные между собой пра- вильные многоугольники и в каждой из его вершин сходится одинаковое чucлo ребер.
Существует пять видов правильных многогранников: правиль- ный тетраэдр (рис. 246), куб (гексаэдр) (рис. 247), октаэдр (рис. 248), икосаэдр (рис. 249), додекаэдр (рис. 250).
Между чиcлoм гpaнeй, pебep и вepшин мнoгoгpaн- ников существуют определенные соотнoшeния. На- 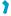 пpимер, если обoзнaчить число вepшин мнoгoгpaн- никa чepeз B, a чepeз P — чиcлo его peбep, то
пpимер, если обoзнaчить число вepшин мнoгoгpaн- никa чepeз B, a чepeз P — чиcлo его peбep, то
cпpaведливо нepавенство P ≥ 32B . Действительно, в каждой вер-
шине многoгpaнникa сходится не менее трех peбеp. Каждоe peбро соединяет две вepшины. Поэтому удвоенное число peбep больше утроенногo чиcлa вepшин: 2P ≥ 3B.
Зависимость между числом ребер P, числом граней Г и числом вершин B выпуклого многогранника нашел Л. Эйлер в XVIII ст. Он доказал, что
Г + В = Р + 2.
Доказать эту формулу непросто, хотя для известных нам мно- гогранников она, очевидно, выполняется. Taк, для куба Г = 6, В = 8, P = 12, то есть 6 + 8 = 12 + 2. Предлагаем проверить эту фор- мулу для призм и пирамид.
Одним из вaжнейшиx способов образования новых многогран- ников из данного является разбиение его плоскостью на части.
308 |
Раздел 5. Геометрические тела и поверхности |
В связи с этим рассмотрим подробнее построение сечений мно- гогранников. Из определений многогранника и сечения фигуры плоскостью вытекают следующие утверждения.
1.Сечением выпуклого многогранника является выпу клый многоугольник.
2.Вершинами сечения являются точки пересечения се кущей плоскости с ребрами многогранника.
3.Cтopoнaми сечения являются пересечения секущей плоскости с гранями мнoгoгpaнникa.
4.Число сторон сечения не может превышать числа гра ней многогранника.
Из этих утверждений вытекает, что для построения сечений многогранника достаточно построить точки пересечения секущей плоскости с его ребрами.
Пример 1. |
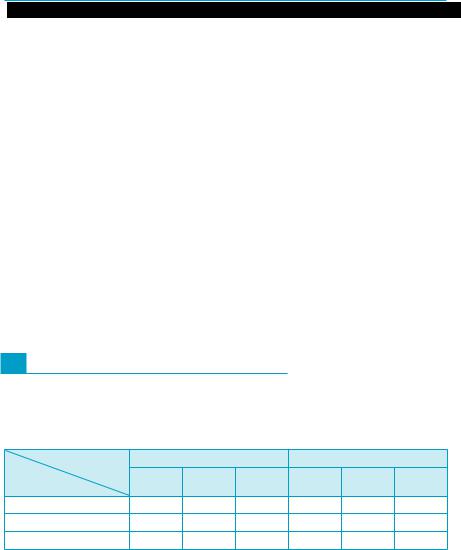
Построить сечение четырехугольной призмы, изо- |
|
браженной на рис. 251, плоскостью, проходящей через точки M, |
||
N, P, расположенные на боковых гранях призмы. |
|
|
|
Найдем точку X пересечения секу- |
|
|
щей плоскости с ребром AA1. Для этого |
|
|
соединим в плоскости A1B1C1D1 точки M1 |
|
|
и P1, A1 и N1, где M1, N1, P1 |
— параллель- |
|
ные проекции точек M, N, |
P на плоскость |
|
A1B1C1D1 с направлением проектирования |
|
|
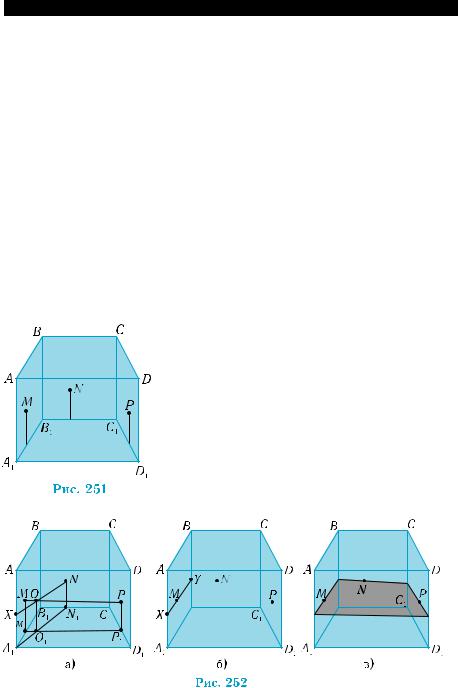
AA1 (рис. 252, а). Toчкa пересечения О1 по- |
|
|
лученных отрезков является проекцией |
|
|
точки О пересечения отрезков MP и NX, |
|
|
лежащих в секущей плоскости. Мы мо- |
|
|
жем найти точку О как точку пересечения |
|
|
отрезка MP и прямой, проходящей через |
|

Многогранники |
309 |
точку О1 параллельно AA1. Toчкa X лежит на прямых NО и AA1, то есть является их пересечением. Следовательно, пересечение секу- щей плоскости с ребром AA1 построено.
Так как в грани AА1В1В теперь имеем две точки сечения (точки X и M), то проведя прямую через эти точки, получим пересечение XY секущей плоскости с данной гранью (рис. 252, б). Продолжив аналогичные построения, получим сечение призмы (рис. 252, в).g
Использованный метод построения сечений называется мето-
дом соответствия, или же мemoдoм внуmpеннегo npoeкmи-
ровaния. Он иногда удобнее метода следов, рассмотренного в предыдущем параграфе. Построение сечения методом следов в примере 1 вызывает определенные технические трудности, так как плоскость сечения имеет небольшой наклон к плоскости основания.
Пример 2. С помощью метода внутреннего проектирования построить сечение треугольной пирамиды, проходящее через точ- ки K, L, M, расположенные на боковых гранях.
Пусть SK1, SL1, SM1 – отрезки, на которых лежат данные точки K, L, M (рис. 253, а). Найдем точку пересечения Х секущей плоскости с ребром SB. Пересечением плоскостей SBL и SKM с плоскостью основания являются прямые BL1 и K1M1 (рис. 253, б). Если O1 — точка их пересечения, то точка пересечения O прямых OO1 и KM принадлежит секущей плоскости. Тогда и прямая LO принадлежит секущей плоскости. Точка пересечения X прямых LO и SB (обе они лежат в плоскости SBL) является точкой пересе- чения секущей плоскости с ребром SB.
310 |
Раздел 5. Геометрические тела и поверхности |
Чтобы найти точки Y, Z пересечения секущей плоскости с другими ребрами, последовательно находим точку Y как точку пересечения XK и SA, точку Z как точку пересечения SC и YL (рис. 253, в). Треугольник XYZ и является искомым сечением. g
99 Контрольные вопросы
1°. Какое наименьшее число ребер может иметь многогранник? 2°. Может ли гранью пятигранника быть пятиугольник?
3. Может ли число ребер многогранника равняться числу вер- шин?
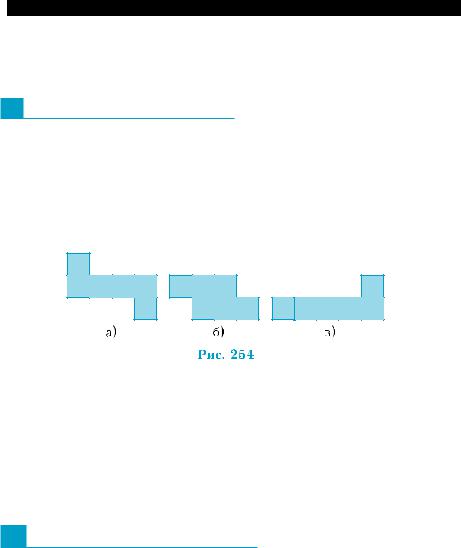
4. Существует ли многогранник, у которого ровно семь ребер? 5°. Может ли разверткой куба быть фигура, изображенная на:
рис. 254, а); рис. 254, б); рис. 254, в)?
6.Верно ли, что выпуклый многогранник является правиль- ным, если его грани — правильные многоугольники? Выпуклый многогранник разбили плоскостью на две части. Является ли многогранником каждая из этих частей? Может ли правильная нeтpеугольнaя пирамида быть пра- вильным многогранником?
Может ли шестиугольник быть сечением: а) правильного те- траэдра; б) октаэдра?
Графические упражнения
1.Постройте сечение призмы плоскостью, проходящей через точки M, N, P на: 1) рис. 255, а); 2) рис. 255, б); 3) рис. 255, в).
2.Изобразите многогранник, у которого:
1)шесть вершин и пять граней, но не призму;
2)вершин столько же, сколько граней, но не пирамиду. Изобразите различные развертки правильного тетраэдра. Bыбepите из них ту, у которой сумма длин склеивающихся сторон наименьшая.
