978-966-10-2413-6_Matematuka 11_rus

условиях, разгрузка определенного типа судов с тем же характе- ром груза, с такой же его упаковкой осуществляется приблизи- тельно в одинаковых условиях.

В-третьих, как мы отмечали выше, исходы этих испытанийнеод- нозначны. Так, при подбрасывании игрального кубика заранее не- известно, какое количество очков выпадет. При покупке лотерейно- го билета предварительно неизвестно, выпадет ли на него выигрыш или не выпадет, а если выпадет, то какой. При извлечении шарика из урны неизвестно, какого цвета он будет.

Наличие всех трех условий делает испытание случайным. Под

случайным испытанием будем понимать любое дейст- вие, которое можно повторить большое количество раз приблизительно в одинаковых условиях и результаты ко-

торого предсказать невозможно.

Для термина «случайное испытание» синонимами являются

случайный эксперимент, случайный опыт.

Пример 1. Какие из следующих испытаний можно считать случайными: 1) стрельба по мишени; 2) нагревание воды в чай- нике; 3) покупка лотерейного билета; 4) вращение рулетки в игре «Поле чудес»; 5) поступление юноши в лицей; 6) многолетние на- блюдения над погодой в тот же день года в одной и той же мест- ности; 7) подбрасывание кнопки; 8) участие команды «Шахтер» в первенстве Украины по футболу?

 Испытания 1), 3), 4), 6), 7) являются случайными, выполня- ются все три отмеченные условия. Предлагаем самостоятельно их проверить. Нагревание воды в чайнике при обычных условиях не является случайным испытанием, так как при 100°С вода за- кипит. Результат известен заранее. Поступление юноши в лицей также не является случайным испытанием, так как его нельзя повторить многократно. Участие команды «Шахтер» в первенст- ве Украины хотя и повторяется многократно, и результат нель- зя предсказать однозначно, не является случайным испытанием, так как меняются условия, в которых происходит это участие. g

Теория вероятностей изучает закономерности, присущие слу- чайным испытаниям. В предыдущих классах вы познакомились с понятием случайного события. Случайные события происходят в результате проведения случайных испытаний. Любой исход

случайного испытания будем называть случайным собы-

тием. В результате такого испытания случайное событие может

412 Раздел7.Элементытеориивероятностей иматематическойстатистики

или произойти, или не произойти. Случайные события будем обо- значать большими латинскими буквами А, В, С, ... . Случайными событиями являются, например, «выпадение четного числа оч- ков» при подбрасывании игрального кубика, «попадание в цель» при выстреле, «выигрыш» при покупке лотерейного билета, «суд- но разгрузили за 10 часов» и т. п.

Ранее мы различали достоверные события (они происходи- ли всегда в испытании), невозможные события (они никогда не происходили в испытании) и случайные. В дальнейшем все со- бытия, связанные со случайными испытаниями, мы будем назы- вать случайными, а невозможные и достоверные рассматривать как их отдельные, крайние, предельные разновидности.

Обращаем внимание на то, что одно и то же собы- тие в одном опыте может быть достоверным, а в другом — невозможным, в третьем – случайным, не

являющимся ни достоверным, ни невозможным.

Пример 2. В урне 3 белых, 3 черных и 3 красных шара. Сколь- ко шаров нужно извлечь из урны, чтобы обязательно иметь шары трех цветов?

 Если извлечь 1 или 2 шара, то невозможно получить шары трех цветов. Если вынуть 7, 8 или 9 шаров, то обязательно по- лучим шары всех трех цветов. Если вынуть 3, 4, 5 или 6 шаров, то возможно, но не обязательно, будем иметь шары трех цветов. g

Ответ. 7, 8 или 9.

Впервом случае мы имели дело с невозможным событи- ем («получить шары трех цветов при извлечении одного или двух шаров») – оно ни в коем случае не происходит в рассмотренной си- туации, во втором случае — с достоверным событием («полу- чить шары трех цветов при извлечении 7, 8 или 9 шаров») — оно обязательно происходит в этой ситуации, в третьем случае — со случайным событием, которое нельзя считать ни достовер- ным, ни невозможным («получить шары трех цветов при извлече- нии 3, 4, 5 или 6 шаров»), — оно может произойти в рассмотренной ситуации, а может и не произойти.

Вэтом примере рассматривались три опыта: извлечение от 1 до 2 шаров, от 3 до 6 шаров, от 7 до 9 шаров. Как видите, одно и то же событие («извлечены шары трех цветов») в третьем испытании является достоверным, в первом — невозможным, во втором – ни достоверным, ни невозможным.

99 Контрольные вопросы

1°. В следующих ситуациях приведите пример случайного собы- тия: а) рождение ребенка; б) игра в баскетбол; в) контроль за качеством изделий; г) участие в лотерее; д) выбор поля фут- больной командой?

2°. Можно ли до проведения случайного испытания однозначно предсказать, наступит ли случайное событие?

3. Можно ли считать, что событие «Петя поступил в лицей» яв- ляется случайным?

4. Можно ли считать, что событие «Космический корабль вышел на заданную орбиту» случайным?

5. Какие из следующих событий нельзя считать ни достоверными, ни невозможными: а) «ученик за контрольную работу получил 8 баллов»; б) «при подбрасывании игрального кубика выпало от 1 до 6 очков»; в) «выпал герб при подбрасывании монеты»; г) «при подбрасывании игрального кубика выпало 7 очков»?

2. Вероятность случайного события

При однократном проведении случайного испыта- ния на появление некоторых случайных событий можно надеяться с большим основанием, чем на появление других. Необходима количественная характеристика шансов наступления некоторого исхода испытания, меры случай- ности события. С такой характеристикой вы знакомы из курса ал- гебры. Речь идет о вероятности события.

Если испытание заканчивается одним из N равно- возможных исходов, из которых N(A) исходов приво- дят к наступлению события А, то вероятностью

N(A) .

N

Вероятность события А обозначается символом Р(А).

Вероятность — от латинского слова probabilitas.

Это определение вероятности события называют классиче- ским. Приведем примеры его применения.

Пример 3. Один раз подброшен игральный кубик. Чему равна вероятность того, что на верхней грани кубика окажется: 1) четное число очков; 2) более двух очков?

414Раздел7.Элементытеориивероятностей иматематическойстатистики

В задаче речь идет о случайном опыте — однократном под- брасывании игрального кубика. Его исходами служат числа оч- ков, которые могут выпасть. Это: 1, 2, 3, 4, 5, 6. Всего их 6: N = 6. Если кубик правильный, симметричен, то есть центр тяжести ку- бика находится в его центре, то эти исходы равновозможны.

1) К событию А — «выпало четное число очков» — приводят

исходы 2, 4, 6, N(A) = 3. Следовательно, P( A) = NN( A) = 36 = 0,5. 2) К событию В — «число выпавших очков больше 2» — приво-

дят исходы 3, 4, 5, 6, N(В)= 4, P(B) = NN(B) = 46 = 32 .

Ответ. 1) 0,5; 2) 32 .

Пример 4. Подбросили две монеты. Какова вероятность того, что: 1) обе они упадут гербом вверх; 2) одна упадет гербом вверх, а другая — цифрой?

 Всего возможны 4 исхода: ГГ, ГЦ, ЦГ, ЦЦ (Г — появление герба, Ц — появление цифры), N = 4. Все они равновозможны (мо- неты считаем симметричными).

1) Обе монеты упадут гербом вверх (событие А) при одном исхо-

де ГГ, N(A) = 1. Поэтому Р(А) = 0,25.

2) Одна монета упадет гербом вверх, а другая — цифрой вверх (событие В) при двух исходах ГЦ или ЦГ, N(В) = 2. Следователь-

но, Р(В)= 42 = 12 . g

Ответ. 1) 0,25; 2) 0,5.

Анализируя решение рассмотренных задач, придем к следую- щей схеме вычисления вероятности события с помощью классиче- ского определения вероятности:

1)выяснить, какой опыт рассматривается в задаче;

2)указать его исходы и вычислить их количество;

3)выяснить, можно ли исходы опыта считать равновозможны- ми, если да, то почему;

4)выяснить, вероятность какого события нужно найти;

5)указать, какие исходы опыта приводят к этому событию или благоприятствуют ему;

6)подсчитать количество исходов опыта, благоприятствующих событию;

7)вычислить вероятность события по рассмотренной формуле.

Классическое определение вероятности позволяет получить простейшие свойства вероятности.

Свойство 1. Вероятность невозможного события равна 0.

 Невозможному событию (будем обозначать его через V) не благоприятствует ни один исход, числитель в формуле для веро-

ятности равен нулю: P(V ) = NN(V ) = N0 = 0. g

Свойство 2. Вероятность достоверного события рав- на 1.

 Достоверному событию (будем обозначать его через U) благо- приятствует каждый исход опыта, числитель равен знаменателю:

N(U) = N =1. g N N

Свойство 3. Вероятность любого случайного собы- тия находится между 0 и 1.

 Для любого случайного события числитель неотрицателен и

не больше знаменателя: 0 ≤ P( A) = N( A) ≤ 1. g

N

Если некоторое событие А не наступает, то говорят, что прои- зошло противоположное ему событие. Ононаступаеттогдаитолько тогда, когда событиеА не наступает.

Событие, которое происходит тогда и только тог- да, когда событие А не происходит, называется про- тивоположным событию A и обозначается А.

Так, в опыте с одним выстрелом в мишень событию A — «попа-

дание в цель» противоположным является событие A — «непопа- дание в цель». В опыте с приобретением лотерейных билетов со- бытию А — «ни один из приобретенных билетов не выиграл»

противоположным является событие A — «хотя бы один из при­ обретенных билетов выиграл».

Понятно, что если событие A противоположно событию А, то

событие А противоположно событию A . События А и A называ-

ются противоположными.

416 Раздел7.Элементытеориивероятностей иматематическойстатистики

Свойство 4. Сумма вероятностей противоположных событий А и A равна 1.

 Очевидно, что N(A) + N( A ) = N, так как при каждом исходе опыта происходит одно и только одно из событий:А или A . Поэтому

N( A) + N( A) = N = 1 , P ( A) + P (A) = 1, или P (A) = 1− P ( A) . g

N N N

Формула классической вероятности предполагает, что исходы опыта равновозможны. Равновозможность исходов является про- явлением симметрии исходов опыта. Симметрия в природе – это и геометрическая симметрия, и разного рода однородность, напри- мер, однородность материала. На вопрос, какие исходы считать равновозможными, математика ответа не дает. Если монета изго- товлена из однородного материала, если она не сточена, если ее

непредубежденно подбросили, то мы вправе считать исходы «вы- падение герба» и «выпадение цифры» равновозможными. Точно так же при подбрасывании «правильного» игрального кубика все шесть исходов данного опыта естественно считать равновозмож- ными. Если из урны с шарами наугад, случайно извлекается шар, причем после каждого извлечения шар возвращается в урну, со- держимое урны тщательно перемешивается, а затем извлекается следующий шар, то мы вправе считать исходы этого эксперимента равновозможными.

Для «неправильного» кубика (например, на одну грань прикре- пили кусочек пластилина) исходы опыта с его подбрасыванием не равновозможны. Так же нельзя считать равновозможными исхо- ды подбрасывания кнопки или пуговицы несимметричной фор- мы, например, с петелькой, или «неправильной» монеты. Если в урне шары различаются массой, то при перемешивании, очевид- но, более тяжелые шары окажутся внизу урны, и исходы опыта с извлечением шара вряд ли можно считать равновозможными.

Если в условии задачи говорится, что выбор каких-то элемен- тов осуществляется наугад, случайно, то это говорит о том, что ис- ходы этого выбора считаются равновозможными.

Проверить предположение о равновозможности исходов опыта можно экспериментально, проведя достаточно большое количест- во опытов. Об этом мы поговорим подробнее в следующем пункте.

99 Контрольные вопросы

1°. Можно ли считать равновозможными следующие исходы опы- тов:

а) «на купленный лотерейный билет выпал выигрыш» и «на купленный лотерейный билет не выпал выигрыш»; б) «из урны с пятью одинаковыми шарами, перенумерованны-

ми числами 1, 2, 3, 4, 5, при извлечении наугад вынут шар №1 и вынут шар №2»; в) «выпал герб» и «выпала цифра» при подбрасывании симме- тричной монеты;

г) «игрок в казино выиграл» и «игрок в казино не выиграл»; д) «промах» и «попадание» у отличного стрелка; е) «выпал герб» и «выпала цифра» при подбрасывании дефор- мированной монеты;

ж) выпало 1, 2, 3, 4, 5, 6 очков при подбрасывании правильно- го игрального кубика; з) выпало 1, 2, 3, 4, 5, 6 очков при подбрасывании деформиро-

ванного игрального кубика?

2. При проведении эксперимента могут наступить 10 равновоз- можных исходов, взаимно исключающих друг друга. Чему равна вероятность события, наступающего:

а) только при одном исходе; б) при каждом из двух определенных исходов?

3. В результате эксперимента происходят равновозможные со- бытия, взаимно исключающие друг друга. Вероятность каж- дого из них равна 0,05. Чему равно число этих событий?

4°. Петя купил один билет лотереи, в которой разыгрывается 10 призов и выпущено 120 билетов. Какова вероятность того, что он выиграет приз?

5. Из ящика, который содержит белые и черные шары, вынима- ют четыре шара. Какое событие противоположно событию: а) «вынут хотя бы один белый шар»; б) «вынуто более двух белых шаров»; в) «среди вынутых шаров белых нет»?

418 Раздел7.Элементытеориивероятностей иматематическойстатистики

3. Относительная частота случайного события

Классическое определение вероятности имеет огра-

ниченную область применения, так как далеко не всегда в реальных ситуациях можно выделить конеч- ное число равновозможных исходов. Приведем пример. Можно ли,

наблюдая за стрелком-спортсменом, определить, какова у него ве- роятность попадания в мишень? Ответить на этот вопрос с помощью классического определения невозможно. В данном случае рассма- тривается случайный опыт – стрельба по мишени, у него два исхо- да: попал в мишень и не попал. Однако эти исходы нельзя считать равновозможными, поэтому нельзя применить классическое опреде- ление вероятности. В подобных случаях применим так называемый статистический подход. Он основан на понятии относительной частоты события. Напомним его определение.

Число опытов, в которых произошло некоторое со- бытие, называется частотой этого события. Отно- шение числа опытов, в которых произошло некото- рое событие, к общему числу опытов, проведенных в одних и тех же условиях, называется относитель- ной частотой этого события.

Будем обозначать относительную частоту случайного события А через n(А). Если проведено n опытов, в n(A) из которых наступило

событие А, то ν( A) = n(nA) . Например, пусть игральный кубик под-

бросили 150 раз, причем 1 очко на верхней грани появилось 26 раз. Здесь 26 – это частота события «выпало 1 очко», а отношение

15026 ≈ 0,173 — относительная частота этого события. В предыдущем

абзаце, выделенном жирным шрифтом, 219 букв. Буква «о» там встречается 44 раза, то есть частота появления буквы «о» в этом от-

рывке текста равна 44, а относительная частота — 21944 ≈ 0,201.

Относительную частоту события иногда выражают в процен- тах. В рассмотренных примерах имеем: относительная частота выпадения одного очка при 150 подбрасываниях игрального ку- бика приближенно равна 17,3 %; относительная частота появле- ния буквы «о» в выделенном отрезке текста приближенно равна

20,1 %.

Из определения относительной частоты события вытекают ее простейшие свойства.

Свойство 1. Относительная частота невоз- можного события равна 0.

 Невозможное событие V не происходит ни в одном из п опы- тов, числитель в формуле для относительной частоты равен нулю,

поэтому ν(V ) = n0 = 0. g

Свойство 2. Относительная частота достоверного события равна 1.

 Достоверное событие U наступает в каждом из п опытов, чи- слитель равен знаменателю: ν(U) = nn = 1. g

Свойство 3. Относительная частота любого случай- ного события находится между 0 и 1.

 Для произвольного события А числитель в формуле для от- носительной частоты неотрицателен и не больше знаменателя:

0 ≤ ν( A) = n(nA) ≤ nn = 1 . g

Свойство 4. Сумма относительных частот противо- положных событий равна 1.

 Понятно, что n( A) + n(A) = n , так как в каждом опыте проис-

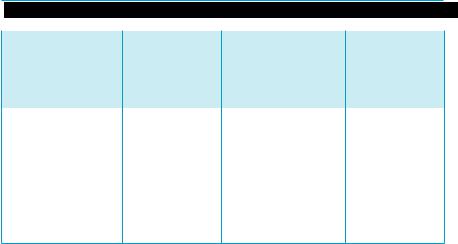
Приведенные свойства относительной частоты совпадают с простейшими свойствами вероятности, рассмотренными в преды- дущем пункте. Этот факт наталкивает нас на вывод о том, что относительную частоту события можно рассматривать как оценку (приближенное значение) его вероятности. В пользу этого вывода говорят результаты опытов с подбрасыванием монеты, проведен- ных многими исследователями (см. таблицу 52).

420 Раздел7.Элементытеориивероятностей иматематическойстатистики

Эти данные показывают, что относительная частота появле- ния любой стороны монеты близка к 0,5, то есть к вероятности события А. Заметим, что из этой таблицы видно, что от серии опы- тов к серии относительные частоты события «выпал герб» меня- лись, но они группировались около одного и того же числа 0,500, хотя практически ни одна из них в точности не равнялась 0,500.

Такие опыты называют статистически устойчивыми. Обра-

тите внимание также на то, что каждый исследователь проводил большое количество опытов. Итак, относительную частоту собы- тия можно принять в качестве оценки ее вероятности, если:

1) число опытов достаточно велико;

2) опыты статистически устойчивы.

Относительную частоту события можно использовать для эк- спериментальной проверки предположения о равновозможности исходов опыта.

Итак, с одной стороны, результаты экспериментов позволяют проверить, насколько можно доверять теоретическим выводам, а с другой стороны — сравнивать, оценивать шансы в тех случаях, когда все исходы опыта перебрать нельзя, или если они имеют различные шансы.

В статистическом подходе к оцениванию вероятности события важным является понятие статистической устойчивости опыта. Относительная частота событий, подсчитанная по результатам статистически устойчивых опытов, мало и не систематически из- меняется от одной серии опытов к другой и, вообще говоря, коле- блется тем меньше, чем больше проведено наблюдений, по кото-