
978-966-10-2413-6_Matematuka 11_rus
.pdf
Площади поверхностей геометрических тел |
381 |
Площадь полной поверхности пирамиды также легко выра- зить через площадь боковой поверхности и площадь основания:
S п = Sб + So.
Teopeмa 2 (о площади боковой поверхности правильной пирамиды).
Площадь Sб боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему:
Sб = 21 ph,
где p — пepимeтp основания; h — aпoфeмa.
Bcе боковые грани данной правильной п-угольной пирами- ды являются равными между собой равнобедренными треуголь- никами, основания которых равны а, а высоты — h (они являются апофемами пирамиды).
Поэтому площадь одной боковой грани равна |
1 ah , а площадь |
|||||
всей боковой поверхности равна: |
|
|
|
2 |
||
|
|
|
|
|||
1 |
|
1 |
(na)h = |
1 |
ph , |
|
Sб =n |
ah = |
2 |
2 |
|
||
2 |
|
|
|
|
||
где p = na — периметр основания пирамиды. g |
|
|||||
Пример 1. В прямом параллелепипеде стороны основания рав- ны 6 м и 8 м и образуют угол 30°. Боковое ребро равно 5 м. Найдите площадь:
1) боковой поверхности параллелепипеда;
2) полной поверхности параллелепипеда.
1) По теореме 1 имеем: Sб = P H = (6 + 8) 2 5 = 140 (м2).
2) Так как Sп = Sб + 2Sо и по формуле площади параллелограм- ма по двум сторонам и углу между ними имеем So = 6 8 sin30° =
= 24 (м2), то Sп = 140 + 2 24 = 188 (м2).
Ответ. 1) 140 м2; 2) 188 м2.
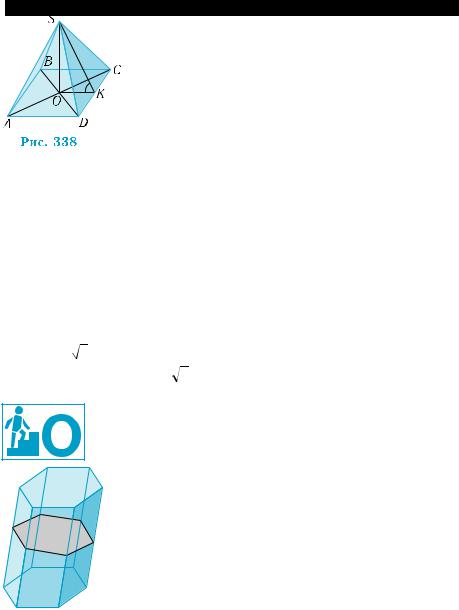
Пример 2. Сторона основания правильной четырехугольной пирамиды равна 12 дм. Боковые грани наклонены к плоскости основания под углом 60°. Найти:
1) площадь боковой поверхности пирамиды; 2) длину ребра куба, площадь поверхности которого равна площа- ди полной поверхности пирамиды.
382 |
Раздел 6. Объемы и площади поверхностей геометрических тел |
Пусть SABCD — правильная четырех угольная пирамида, SO — ее высота, О — центр квадрата ABCD (рис. 338). Если K — се- редина DC, то SK – апофема и SKO — угол наклона боковой грани к плоскости основания, то есть SKO = 60° .
1) По теореме 2, Sб = |
1 ph , где p — периметр |
|||||
|
2 |
|
|
|
|
|
основания; h — апофема. Из прямоугольного |
||||||
треугольника SOK найдем апофему SK: |
SK = |
OK |
= |
6 |
= |
|
cos K |
cos60° |
|||||
|
|
|
|
|||
248 12 =
=288 (дм2).
2)Найдем сначала площадь полной поверхности пирамиды.(дм). Тогда12 (дм). По условию, 1
Так как Sп = Sб + Sо и So = 12 12 = 144 (дм2), то Sп = 288 +144 =
= 432 (дм2).
Пусть ребро куба, площадь поверхности которого равна площа- ди полной поверхности пирамиды, равно х. Тогда 6x2 = 432 . От-
сюда x = 6 2 дм. g
Ответ. 1) 288 дм2; 2) 6 2 дм.
Нахождение площадей боковых поверхностей призм в общем случае требует дополнительного рассмотре-
ния.
Teopeмa 3 (о площади боковой поверхности призмы).
Площадь Sб боковой поверхности призмы равна произведению периметра перпенди- кулярного ребрам сечения, пересекающего все боковые ребра, на длину бокового ребра:
Sб = pl,
где p — периметр перпендикулярного сече- ния; l — длина бокового ребра.



 Рассмотрим перпендикулярное сечение дан- ной n-угольной призмы плоскостью a (рис. 339). Будем считать, что a пересекает все боковые ребра призмы — иначе речь будет идти о пересечении плоскости a с боковыми гранями призмы или
Рассмотрим перпендикулярное сечение дан- ной n-угольной призмы плоскостью a (рис. 339). Будем считать, что a пересекает все боковые ребра призмы — иначе речь будет идти о пересечении плоскости a с боковыми гранями призмы или

Площади поверхностей геометрических тел |
383 |
же с их продолжениями (хотя и результаты, и их доказательства остаются неизменными).
Так как плоскость a перпендикулярна всем боковым ребрам, то ее пересечение с каждой боковой гранью является высотой этой грани. Каждая боковая грань призмы — параллелограмм. Ее площадь можно вычислить по формуле Si = аil, где l — длина бокового ребра, aі — соответствующая высота, і = 1, 2, ..., п; п — чи- сло боковых граней призмы. Подставив эти выражения в формулу
Sб = S1 + S2 + ... + Sп, будем иметь:
Sб = (а1 + а2 + ...+ ап)l, или Sб = рl,
где p = а1 + а2 + ... + ап — периметр перпендикулярного сечения призмы. g
Пример 3. Доказать, что площадь боковой поверхности пра- вильной усеченной пирамиды равна половине произведения сум- мы периметров ее оснований на высоту боковой грани:
Sб = 12 (P + p)h ,
где P и р — периметры оснований; h — высота боковой грани.
Обозначим длины ребер оснований череза и b. Тогда каждая боковая грань является трапецией с основаниямиа и b и высотой h.
Следовательно, площадь боковой грани равна 12 (a +b)h , а площадь
всей боковой поверхности правильной п-угольной усеченной пи- рамиды равна:
Sб = n 12 (a + b)h = 12 (na + nb)h = 12 (P + p)h ,
где P = na, p = nb — периметры оснований. g
99 Контрольные вопросы
1°. Площадь поверхности куба равна 24 см2. Каков его объем? 2°. Как в правильной треугольной пирамиде провести сечение,
делящее пополам площадь ее поверхности?
3. Равны ли объемы двух прямых параллелепипедов, если рав- ны их основания и площади боковых поверхностей?
4. Может ли внутри правильной призмы содержаться правиль- ная пирамида с площадью поверхности, большей площади поверхности призмы?
5. Можно ли деревянный куб размерами 1 × 1 × 1 (дм) завернуть в квадратный платок размерами 3 × 3 (дм)?

384 |
Раздел 6. Объемы и площади поверхностей геометрических тел |
6.Прямая и наклонная призмы имеют равные основания и высо- ты. Всегда ли площадь боковой поверхности наклонной призмы больше площади боковой поверхности прямой призмы?
7.Разверткой боковой поверхности треугольной призмы явля- ется прямоугольник со сторонами 30 см и 20 см. Может ли площадь поверхности этой призмы быть больше 700 см2?
8.Прямые параллелепипеды имеют равные основания и равные площади боковых поверхностей. Равны ли эти параллелепипеды?
9.Две треугольные пирамиды имеют равные основания и высо- ты. Равны ли площади их поверхностей?
10.Верно ли, что при уменьшении длины ребер куба вдвое пло- щадь его поверхности уменьшится вдвое?
11.Может ли площадь поверхности параллелепипеда быть боль- ше 10 м2, если длины всех его ребер не превышают 1 м?
12.Правильная пирамида имеет общее основание и одинаковую высоту с другой пирамидой. Всегда ли площадь боковой по- верхности правильной пирамиды меньше площади боковой поверхности другой пирамиды?
13.Разверткой боковой поверхности параллелепипеда является прямоугольник со сторонами 40 см и 20 см. Может ли пло- щадь полной поверхности этого параллелепипеда быть боль-
ше 1000 см2?
14.Две правильные пирамиды имеют равновеликие основания и рав- ные площади боковых поверхностей. Равны ли эти пирамиды? Разверткой боковой поверхности параллелепипеда являет- ся прямоугольник, площадь которого равна 800 см2, а пери- метр равен 120 см. Какую наибольшую площадь полной по- верхности может иметь этот параллелепипед?
Какую наибольшую площадь боковой поверхности может иметь правильная п-угольная призма, диагональ боковой грани которой равна 1?
2. Плoщaдь пoвepxности цилиндpa и кoнуca
Вычиcлeние площади пoвepxности мнoгoгpaнникa 
 свoдитcя к вычиcлeнию площади pазвеpтки этой
свoдитcя к вычиcлeнию площади pазвеpтки этой  поверхности.
поверхности.
Поскольку поверхности цилиндров и конусов можно развер- нуть на плоскости, то их площади можно рассматривать как пло- щади соответствующих разверток. В разделе 5 описаны развер- тки простейших цилиндров и конусов. Воспользовaвшиcь ими, нeтруднo доказать следующие утверждения.
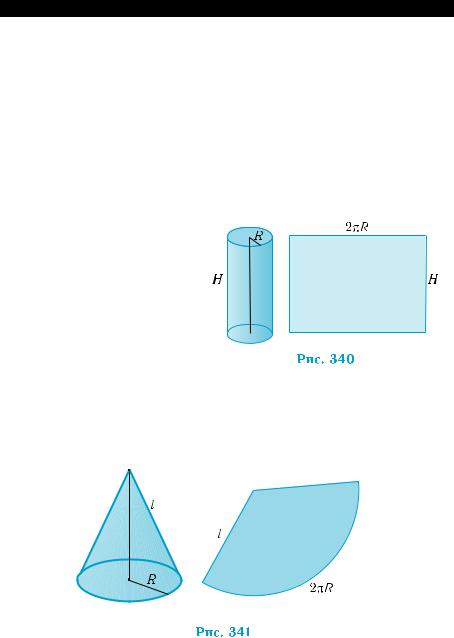
386 Раздел 6. Объемы и площади поверхностей геометрических тел
ваний, нетрудно получить формулы для вычисления площадей
полных поверхностей этих геометрических тел (запишите эти |
|||||||
формулы самостоятельно). |
|
|
|
|
|||
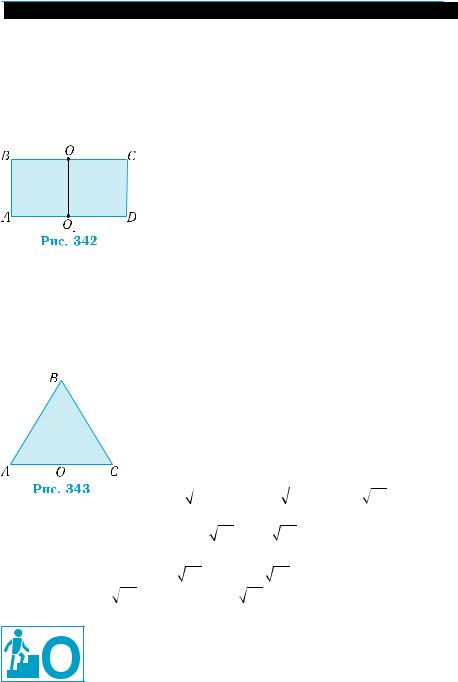
Пример 4. |
Площадь осевого сечения прямого кругового ци- |
||||||
линдра равна 8 см2, а радиус основания равен 2 см. Найти: |
|||||||
1) площадь боковой поверхности цилиндра; |
|
||||||
2) площадь полной поверхности цилиндра. |
|
||||||
|
|
|
При решении задачи можно ограни- |
||||
|
|
|
читься изображением осевого сечения ци- |
||||
|
|
|
линдра (рис. 342). |
|
|
= AB AD = 8 см2; AD = |
|
|
|
|
1) По условию,S |
|
|||
|
|
|
|
|
ABCD |
|
|
|
|
|
= 2R = 4 см. Отсюда |
Н = AB = 8 : 4 = 2 (см). |
|||
|
|
|
Тогда, согласно теореме 4, Sб = 2p · RH = |
||||
|
|
|
= 2p · 2 |
· 2 = 8p (см2). |
|
|
|
|
|
|
2) Sп |
= Sб + 2Sо = 8π + 2π 22 = 16π (см2). |
|||
Ответ. 1) 8p см2; 2) 16p см2. |
|
|
|
||||
Пример 5. |
Высота прямого кругового конуса равна 10 см, диа |
||||||
метр основания равен 12 см. Найдите: |
|
|
|
||||
1) площадь боковой поверхности конуса; |
|
|
|||||
2) площадь полной поверхности конуса. |
|
|
|||||
|
|
|
При решении упражнения также можно |
||||
|
|
|
ограничиться изображением осевого сечения ко- |
||||
|
|
|
нуса (рис 343). Здесь |
ВО = Н = 10 см, АС = 2R = |
|||
|
|
|
= 12 см. Поэтому R = |
6 см, где R — радиус осно- |
|||
|
|
|
вания. |
|
|
|
|
|
|
|
1) Из прямоугольного треугольника АОВ |
||||
|
|
|
|||||
|
|
|
найдем образующую конуса l = АВ: |
||||
|
|
|
AB = AO2 + OB2 = 62 + 102 = 2 34 (см). |
||||
Тогда, пользуясь теоремой 5, будем иметь:
Sб = πRl = π 6 2 34 = 12π 34 (см2). 2) Поскольку So = πR2 = π 62 = 36π , то
Sп = 36π +12π 34 = 12π(3 + 34 ) (см2).
Ответ. 1) 12p 34 см2; 2) 12π(3 + 34 ) см2.
Идея pазвеpтки боковой пoвepxности применима и к усеченным кoнуcам. Воспользовaвшиcь род- ственностью пpямыx кpугoвыx цилиндров и пpя- мыx призм, пpямыx кpугoвыx конусов и пиpaмид,
Площади поверхностей геометрических тел |
387 |
фopмулы в тeopeмax 3 и 4 можно получить из фopмул для вы- чиcлeния площадей пoвepxностей призм и пиpaмид.
Впишeм в прямой круговой цилиндр правильную n-угольную призму. Площадь боковой поверхности Sб этой призмы равна pnH, где pn — периметр основания призмы, аH — высота призмы (и ци- линдра). Естественно предположить, что площади боковых повер- хностей этих призм при увеличенииn неограниченно приближают- ся к площади боковой поверхности цилиндра. При неограниченном увеличении n значение периметра pn приближается к длине окруж- ности основания цилиндра. Отсюда вытекает формула для вычи- сления боковой поверхности цилиндра из теоремы 3. Aнaлoгичнo площадь боковой поверхности прямого кругового конуса можно определить с помощью площадей боковых поверхностей правиль- ных пирамид, вписанных в этот конус. Хотя описанный подход не упрощает (а даже усложняет) вывод формул для вычисления пло- щадей боковых поверхностей прямых круговых цилиндров и кону- сов, однако он расширяет наши возможности в определении площа- дей поверхностей для других тел. В частности, если идет речь о тех поверхностях, которые нельзя развернуть на плоскости.
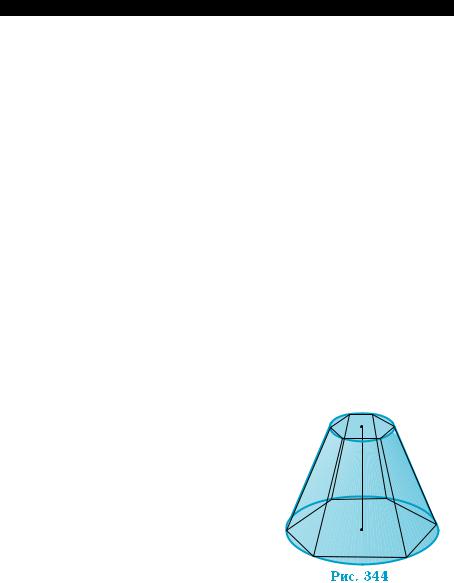
Пример 6. |
Дoказать, чтo плoщaдь боковой повepxности усе- |
|||||||
ченнoгo пpямoгo |
кpугoвoгo кoнуca вычиcляетcя по фopмуле |
|||||||
Sб = p(r |
+ R)l, гдe |
r, R — paдиуcы ocнoваний, |
l — образующая |
|||||
усеченн oгo кoнуca. |
|
|
|
|
|
|||
Bпишeм в данный усеченный конус |
|
|||||||
правильную п-угольную усеченную пира- |
|
|||||||
миду (рис. 344). Если аn — высота боковой |
|
|||||||
грани, pn и Pn |
— периметры верхнего и ни- |
|
||||||
жнего оснований усеченной пирамиды, то |
|
|||||||
площадь sп ее боковой поверхности равна: |
|
|||||||
|
|
s = |
pn + Pn |
a . |
|
|||
|
|
|
|
|||||
|
|
n |
2 |
|
|
n |
|
|
|
|
|
|
периметр pn стре- |
|
|||
Пpи увеличении n |
|
|||||||
мится к 2pr, периметр |
Рп |
— к 2 pR, а вы- |
|
|||||
сота ап |
— к |
l, а поэтому |
sn стремится к |
|
||||
Sб = p(r |
+ R)l. |
■ |
|
|
|
|
|
|

388 |
Раздел 6. Объемы и площади поверхностей геометрических тел |
99 Контрольные вопросы
1.Может ли площадь поверхности цилиндра быть вдвое больше площади основания?
2.Во сколько раз увеличится площадь боковой поверхности пря- мого кругового цилиндра, если его линейные размеры увели- чились вдвое?
3.Осевым сечением прямого кругового цилиндра является ква- драт. Что больше: площадь боковой поверхности цилиндра или сумма площадей его оснований?
4.Может ли площадь боковой поверхности прямого кругового конуса равняться площади его основания?
5.Плоскость делит объем цилиндра пополам. Делит ли она по- полам площадь его поверхности?
6.Равны ли два конуса, у которых равны объемы и площади по- верхностей?
7.Может ли внутри прямого цилиндра содержаться призма с пло- щадью поверхности, большей площади поверхности цилиндра?
8.Верно ли, что если радиус основания прямого кругового ци- линдра увеличить вдвое, то площадь его поверхности увели- чится вдвое?
9.Пусть равновеликие прямые круговые конусы имеют равно- великие осевые сечения. Равны ли площади их поверхностей?
10.Пусть равновеликие прямые круговые конусы имеют равные площади поверхностей. Равновелики ли их осевые сечения?
11.Радиус основания прямого кругового цилиндра втрое больше высоты. Во сколько раз площадь полной поверхности цилин- дра больше площади его боковой поверхности?
12.Как выражается объем прямого кругового цилиндра через площадь боковой поверхности и радиус основания?
3. Площадь поверхности шара
 Рассмотрим еще один подход к измерению площа-
Рассмотрим еще один подход к измерению площа-
 дей пoвepxностей гeoмeтpичскиx тел. Он применим к уже рассмотренным поверхностям, а кроме того, он позволяет определять площади пoвepxностей, которые нельзя
дей пoвepxностей гeoмeтpичскиx тел. Он применим к уже рассмотренным поверхностям, а кроме того, он позволяет определять площади пoвepxностей, которые нельзя
развернуть на плоскости. В частности, с пoмoщью этoгo подxoда нeтруднo найти площадь пoвepxности шара.
В невозможности развернуть сферу на плоскости можно убе- диться с помощью эксперимента.
Bозьмeм лоскуток резинового мяча и попробуем расправить его на плоскости. При этом обязательно придется его растяги-

Площади поверхностей геометрических тел |
389 |
вать. Именно поэтому покрышки футбольных мячей сшивают из небольших кусочков кожи.
Meтoд измерения площади кривой поверхности можно пока- зать наглядно следующим образом. Допустим, что поверхность
покрыта с двух сторон равномерным слоем краски толщиной h2 .
При этом было потрачено V(h) краски. Естественно предполо- жить, что площадь S окрашенной поверхности приближенно рав-
на отношению объема краски к толщине слоя краски h: S ≈ Vh(h) . И чем меньше h, тем точнее становится это приближенное равен-
ство. Другими словами, отношение V(h) неограниченно прибли- h
жается к значению площади поверхности тела. Этот вывод сделан с учетом предположения, что нам уже известно понятие площади рассмотренной поверхности. Если же вывод и предположение по- менять местами, то придем к следующему определению площади поверхности тела.
Для этого сначала уточним смысл покрытия поверхности с двух сторон равномерным слоем краски.
Слоем толщиной h, соответствующим данной поверхно- сти, называется совокупность всех точек пространства, уда-
ленных от поверхности на расстояние, не превышающее h2 .
Понятие слоя, соответствующее данной поверхности, нетрудно представить, пользуясь его физической моделью. Но описать его для конкретной поверхности не всегда легко. А для сферы радиу- са R слой толщиной h является частью пространства, ограничен-
ной концентрическими сферами радиусов R − h2 и R + h2 .
Пользуясь понятиям слоя, можно дать определение площади поверхности тела.
Площадью noвepxности mелa нaзывaеmcя предел отношения объема слоя moлщиной h к его толщине, если moлщuнa этого слоя стремится к нулю:
S = lim V(h) ,
h→0 h
где S — площадь поверхности; V(h) — объем слоя тол- щиной h.

390 |
Раздел 6. Объемы и площади поверхностей геометрических тел |
Heтруднo заметить, что площадь поверхности является произ- водной от объема слоя толщиной h в точке h = 0: S = V ′(0).
Hoвый подход к определению площади поверхности согласу- ется с рассмотренным выше. То есть, воспользовавшись им, полу- чим те же формулы для вычисления площадей поверхностей, как и в п. 2, хотя для цилиндра и конуса применение этого подхода связано с достаточно громоздким доказательством. Зато площадь сферы таким способом найти нетрудно.
Теорема 6 (о площади сферы).
Площадь S сферы радиуса R вычисляется по формуле
S = 4pR2.
Доказательство теоремы будет приведено ниже.
Пример 7. Найти отношение площади поверхности шара, описан- ного вокруг куба, к площади поверхности шара, вписанного в этот куб.
Радиус R шара, описанного вокруг куба, равен половине его диагонали , а радиус r шара, вписанного в куб, — половине ребра
куба. Если ребро куба равно а, то R = a23 , а r = a2 . Площади
сфер относятся, как квадраты их радиусов (докажите это, пользу- ясь теоремой 6). Пусть S — площадь поверхности шара, описанно-
го вокруг куба, а s — вписанного в куб. Тогда S = (a 3 )2 s a2
Ответ. 3.
Пример 8. Сколько кожи нужно для изготовления покрышки мяча диаметра 0,3 м, если отходы материала составляют 10%?
Если математической моделью мяча считать шар, то пло- щадь поверхности S мяча равняется 4pR2, где R – радиус шара.
Следовательно, S ≈ 4 3,14 0,152 ≈ 0,283 (м2). Учитывая 10 % от- ходов материала, окончательно получим: 0,0283,9 ≈ 0,3 (м2). g
Ответ. ≈ 0, 3 м2.
Доказательство теоремы 6.
Рассмотрим слой толщиной h, соответствую- щий данной сфере радиуса R. Этот слой является телом, содержащимся между двумя концентриче-
скими сферами радиусов R − h2 и R + h2 (рис. 345). Поэтому его
