978-966-10-2413-6_Matematuka 11_rus

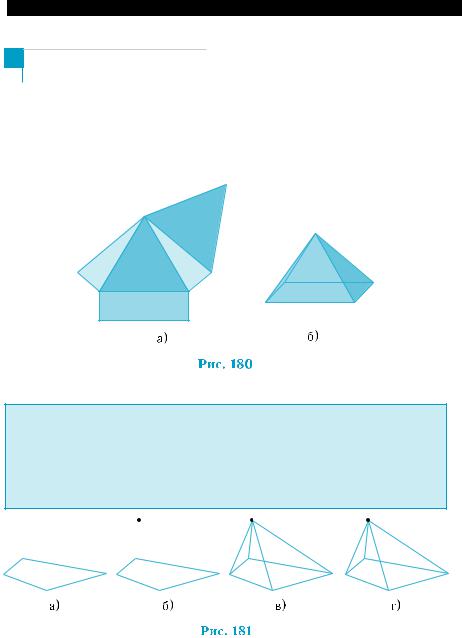
ный многоугольник — основанием пирамиды, а данная точ-

ка — ее вершиной (рис. 177, г).

Пирамида — от греческого πυραµις (pyramis), возможно от египетского per me ous — боковое ребро сооружения.

В зависимости от количества сторон основания различают тре­ угольные, четырехугольные, ...,п-угольные пирамиды (рис. 178, а–г).

!Напомним, треугольную пирамиду называют еще тет­ раэдром­ .

Тетраэдр — от греческих tetrarez (tettares) – четыре, в сложных словах — (tetra-) и ezra (hedra) — основание, поверхность, сторона — четырехгранник, все грани которого треугольники.

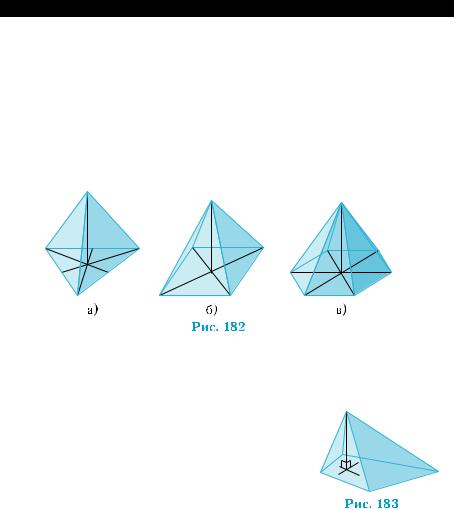
Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми ре- брами пирамиды. Стороны основания пирамиды также считаются ребрами пирамиды. Отрезки, со- единяющие вершину пирамиды со всеми точками произвольной стороны основания, образуют тре­ угольник (рис. 179), который называется боковой

Пирамидa нaзывaеmcя npaвuльнoй, если ее ocнoвани- ем является npaвuльный мнoгoугольнuк, а вepшuнa opmoгoнaльнo npoeкmируеmcя в цeнmp этoгo мнoгo­

угольнuкa.

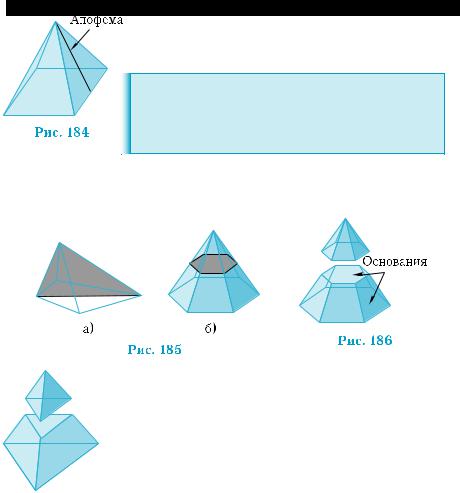
При изображении правильной пирамиды изображением вер- шины служит конец перпендикуляра к плоскости основания, проведенного из изображения центра основания. Вертикаль- ность этого отрезка подчеркивает правильность пирамиды. На рис. 182, а), б), в) изображены правильные треугольная, четырех­ угольная и шестиугольная пирамиды.

Правильная треугольная пирамида, все грани которой явля- ются равными треугольниками, называется правильным те-

траэдром.

Расстояние от вершины пирамиды до пло- скости основания называется высотой пи- рамиды. Она равна длине перпендикуляра, проведенного из вершины пирамиды на пло- скость основания (рис. 183). Этот перпендику- ляр также называют высотой пирамиды.

Важнейшие свойства правильных пирамид содержатся в следующем утверждении.

Теорема 1 (о свойствах правильной пирамиды).

В правильной пирамиде боковые ребра равны между собой и одинаково наклонены к плоскости основания, а боковые грани являются равными между собой равнобе­ дренными треугольниками, одинаково наклоненными к плоскости основания.

Доказательство этой теоремы будет приведено ниже.

Высоту боковой грани правильной пира- миды, проведенную из ее вершины, называют

апофемой (рис. 184).

Апофема — от греческого αποτιθηµι

(apotithemi) — откладываю на бок, со - стоит из απο (apo) — от, с, из, и θεµα

(thema) — положенное, поставленное.

Сечение пирамиды с выпуклым основанием плоскостью, про- ходящей через два ее боковых ребра, не лежащих в одной грани, является треугольником (рис. 185, а).

Сечение п-угольной пирамиды плоскостью, па- раллельной основанию, является п-угольником, так как такая плоскость пересекает все боковые ребра пирамиды (рис. 185, б).

Сечение пирамиды плоскостью, параллельной основанию, разбивает пирамиду на две фигуры (рис. 186). Одна из них является пирамидой. Вторую называют усеченной пирамидой. Поверхность

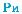
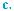
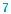п-угольной усеченной пирамиды состоит из двух многоугольников, которые называют основаниями, и п трапеций (почему?), которые называют боковыми гранями. Усеченная пи- рамида, полученная из правильной пирамиды, также называется правильной. Боковые грани правильной усеченной пирамиды яв- ляются равными равнобокими трапециями (рис. 187).

Пример 1. Боковое ребро правильной четырехугольной пира- миды со стороной основания 8 см наклонено к плоскости основа- ния под углом 60°. Найти: 1) высоту пирамиды; 2) апофему пира- миды; 3) угол наклона боковой грани к плоскости основания;

4) площадь сечения пирамиды плоскостью, проходящей через се-

редины смежных ребер основания пирамиды перпендикулярно

основанию.

 Построим изображение данной пирами- ды SABCD (рис. 188). Основанием пирамиды

является квадрат ABCD со стороной 8 см, О — точка пересечения диагоналей основания. По

свойствам правильной пирамиды, SO ^ ABCD,

SA = SB = SC = SD, SAO = SBO = SCO = = SDO = 60°. Пользуясь приведенными дан-

точкамиМиN (рис. 190). ТреугольникМРNявляется искомым сече- нием. Действительно, РN || SА, РМ || SC, по свойству средней линии

треугольника. По признаку параллельности плоскостей, плоскости МРN и АSС параллельны. Так как плоскость АSС проходит через перпендикуляр SО к плоскости основания, то она перпендикулярна

ные треугольники с равными боковыми сторонами. Основания этих треугольников также равны, так как они являются сторо- нами правильного многоугольника. Поэтому боковыми гранями пирамиды являются равные между собой равнобедренные треуголь- ники. Угол наклона граниA1SA2 к плоскости основания измеряется линейным углом SM1O, где M1 — середина ребра А1А2; SM1 ^ A1A2, OM1 ^ A1A2. Анaлoгичную роль играет угол SM2O для грани A2SA3, где M2 — середина ребра A2A3. Так как треугольники SM1O и SM2O равны между собой (докажите это), то равными являются и углы SM1O и SM2O. To есть боковые грани A1SA2 и A2SA3 одинаково на- клонены к плоскости основания.g

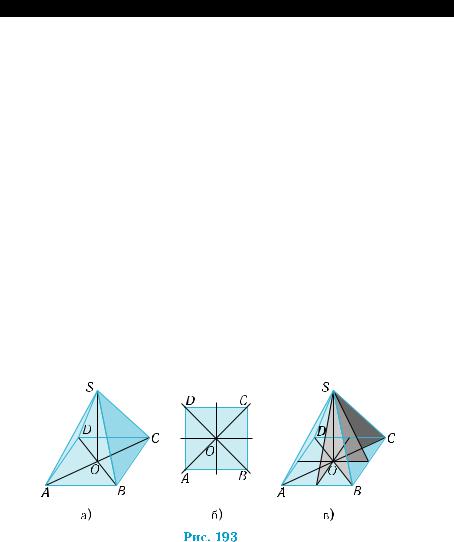
Правильные пирамиды обладают свойствами симметрии, определяемыми свойствами симметрии их оснований. Напри- мер, основанием правильной четырехугольной пирамиды явля- ется квадрат (рис. 193, а). Квадрат имеет четыре оси симметрии (рис. 193, б), каждая из них определяет плоскость симметрии пи- рамиды, проходящую через высоту пирамиды SO (рис. 193, в). Не- трудно убедиться в том, что прямая SO является осью симметрии пирамиды SABCD, так как точка O является центром симметрии основания. Повороты пространства вокруг прямой SO на углы, отображающие основание на себя (90°, 180°, 270°, …), отображают пирамиду SABCD на себя.

Пример 2. Основанием пирамиды является прямоуголь- ник со сторонами 6 см и 8 см. Углы между боковыми ребрами пирамиды и плоскостью основания равны по 60°. Вычислить:

1) высоту пирамиды;

2) боковое ребро пирамиды;

3) высоты боковых граней пирамиды, проведенные из вершины пирамиды; 4) величины двугранных углов при основании пирамиды.

268 Раздел 5. Геометрические тела и поверхности

 Перед построением данной пирамиды SABCD стоит обратить внимание на то, что все ее боковые ребра одинаково наклонены к плоскости основания. Поэтому основание О высоты попадает в центр окружности, опи- санной вокруг прямоугольника, то есть в точ- ку пересечения диагоналей прямоугольника

ABCD (рис. 194).

Пусть АВ = 6 см, ВС = 8 см. Из прямоугольного треугольника ABC имеем: AC = AB2 + BC2 = 62 + 82 =10 (см). Тогда АО =

=12 AC =5 см.

1)Высоту пирамиды SO найдем из прямоугольного треуголь- ника SOA:

tg SAO = 5tg 60° = 5 3 (см).

2) Найдем длину бокового ребра пирамиды из прямоугольного треугольника SOA:

OL = 12 AB =3 см. Высоту SK боковой грани CSD найдем из пря- моугольного треугольника SOK:

Нетрудно убедиться, что противоположные к рассмотренным грани наклонены к основанию под теми же углами. g

Ответ. 1) 5 3 см; 2) 10 см; 3) 91 см; 2 21 см; 4) arctg 543 ; arctg 533 .

99 Koнтpoльные вопросы

1°. Сколько сторон в основании пирамиды, имеющей 9 боковых ребер?

2. Может ли пирамида иметь нечетное количество ребер?

3°. Сколько сторон в основании пирамиды, имеющей: а) 16 ребер; б) 16 граней?

4. Может ли высота пирамиды совпадать с высотой одной из бо- ковых граней?

5°. Может ли сечение четырехугольной пирамиды быть шести­ угольником?

6. Может ли развертка боковой поверхности правильной тре­ угольной пирамиды быть трапецией?

7. Верно ли, что основанием четырехугольной пирамиды, боко- вые грани которой наклонены к плоскости основания под оди- наковыми углами, является квадрат?

8°. Имеет ли правильная треугольная пирамида плоскости сим- метрии, оси симметрии, центр симметрии?

9. Существует ли усеченная пирамида, все ребра которой равны между собой?

2. Конусы

Многие физические тела или их части имеют ко- ническую форму: конец карандаша, «нос» ракеты, крыша башни, террикон (рис. 195, а–г) и т. п.

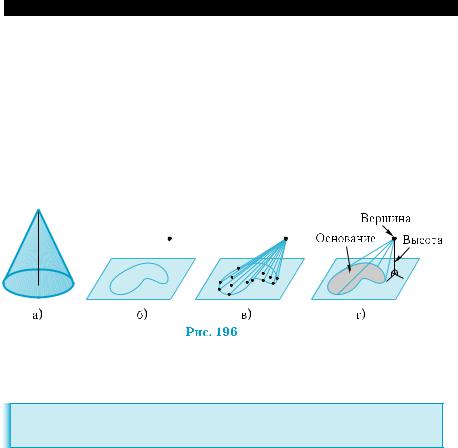
Простейшим конусом является хорошо известный круговой ко- нус (рис. 196, а). Общей особенностью конусов и пирамид является «заостренность», являющаяся следствием их построения. Подоб- но пирамиде, круговой конус можно представить образованным из отрезков, соединяющих точки круга с вершиной конуса. Если отрезки откладывать от точек произвольной плоской фигуры, то получим фигуру, которую также естественно называть конусом.

Пусть даны плоская фигура и точка вне плоскости этой фигуры (рис. 196, б). Соединим отрезками все точки этой фигуры с данной точкой (рис. 196, в). Фигура, состоящая из всех точек построенных отрезков, называется конусом, данная плоская фигура — осно-

ванием конуса, а данная точка — его вершиной (рис. 196, г).

Расстояние от вершины конуса до плоскости его основания назы- ваетсявысотойконуса. Высотой конуса называют также перпенди- куляр, проведенный из вершины конуса к плоскости его основания.

Конус — от греческого χϖνοζ (konos) — остроконечное тело, кегля, верхушка шлема.

Из приведенного определения вытекает, что понятие конуса является обобщением понятия пирамиды. Пирамида – это конус, основанием которого является многоугольник. Поэтому не удиви- тельно, что пирамида с большим количеством сторон основания похожа на обычный конус.

Koнуc, основанием которого является круг, называется кругo- вым. Если высота кругового конуса проходит через центр осно- вания, то конус называется прямым. To есть прямой круговой конус — это обычный конус, который мы рассматривали ранее.

Отрезки, соединяющие вершину кругового конуса с точками окружности основания, называются образующими. Нетрудно увидеть, что образующие прямого кругового конуса равны между собой (докажите).