
978-966-10-2413-6_Matematuka 11_rus
.pdf

172 |
Раздел 3. Производная и ее приложения |
2°. |
Для функции у = f(x), график которой изо- |
|
бражен на рис. 92, укажите интервалы, на |
|
которых f ′(x) > 0, f ′(x) < 0. |
3°. |
Известно, что f ′(x)= х(х + 1). Укажите про- |
|
межутки, на которых функция у = f(x) убы- |
|
вает (возрастает). |
4. |
На рис. 93 изображен график производной |
|
функции у = g(x). Укажите промежутки |
|
возрастания функции у = g(x). |
5. |
Известно, что f ′(x) = g′(x). Какой вид имеет |
|
график функции у = f(x) – g(x)? |
6. |
Чётная дифференцируемая функция возра- |
|
стает на промежутке (0; +∞). Какой знак име- |
|
ет ее производная на промежутке (–∞; 0)? |
|
2. Экстремумы функции |
|
|
При исследовании функции важную роль играют |
|
|
точки, отделяющие промежутки возрастания фун- |
|
|
кции от промежутков убывания. Так, для функции |
|
|
у = f(x), график которой изобра- |
|
|
жен на рис. 94, это точки х1, х2, х3. |
|
|
Исследуем поведение функции в |
|
|
окрестностях этих точек. |
|
|
Нетрудно заметить, что значе- |
|
|
ние функции в точке |
х1 больше |
|
значений функции в |
соседних |
|
точках. Другими словами, для |
|
ности точки |
всех х ≠ х 1 из некоторой окрест- |
|
х1 выполняется неравенство f(x) < f(х1). Аналогично |
||
функция ведет себя в окрестности точки х3. Точки, подобные х1, х3, |
||
называются |
точками максимума функции. |
|
Точка х0 называется точкой максимума функции у = f(x), если для всех х ≠ х0 из некоторой окрестности
этой точки выполняется неравенство f(x) < f(х0).
 Максимум — от латинского maximum — наибольшее.
Максимум — от латинского maximum — наибольшее.
Значение функции в точке х2 меньше всех «соседних» значений функции, то есть можно найти такую окрестность точки х2, что
Исследование функций и построение их графиков с помощью производной |
173 |
для всех х ≠ х2 из этой окрестности будет выполняться неравенство f(x) > f(х2).
Точка х0 называется точкой минимума функции у = f(x), если для всех х ≠ х0 из некоторой окрестности
этой точки выполняется неравенство f(x) > f(х0).
 Минимум — от латинского minimum — наименьшее.
Минимум — от латинского minimum — наименьшее.
Для точек максимума и минимума есть общее название – точ-
ки экстремума, или точки локального экстремума.
Экстремум — от латинского extremum — крайнее, последнее.
Локальный — от латинского locаlis — местный, ограниченный.
Употребляя термин «локальный», мы этим самым подчеркну- ли, что наличие экстремума функции в точке х0 зависит только от поведения функции вблизи этой точки. Действительно, для фун- кции у = f(x) (см. рис. 94) неравенство f(x) < f(х1) выполняется на интервале (с; d), но не выполняется на всей области определения. Например, f(x3) > f(х1). Может даже случиться, что значение фун- кции в точке минимума будет больше значения функции в точке максимума, подобно тому, как впадина в горах может быть выше над уровнем моря, чем небольшая вершина.
Выясним теперь, как можно найти точки экстремума функции. Рассмотрим сначала функцию, дифференцируемую в своей об- ласти определения. Обратите внимание на то, что на рис. 94 в точках графикаА, В, Скасательные 
 к графику функции параллельны оси х. Следова-
к графику функции параллельны оси х. Следова-
тельно, если дифференцируемая функция имеет 
 экстремум в точке х0, то производная функции в
экстремум в точке х0, то производная функции в  этой точке равна нулю. Однако, не всегда из того, что производная в точкех0 равна нулю, следует, что х0 — точка экстремума. Например, производная функции у = х3 при х = 0 равна нулю, но эта точка не является точкой экстремума функции (рис. 95).
этой точке равна нулю. Однако, не всегда из того, что производная в точкех0 равна нулю, следует, что х0 — точка экстремума. Например, производная функции у = х3 при х = 0 равна нулю, но эта точка не является точкой экстремума функции (рис. 95).
Возникает вопрос, как из «подозрительных» точек, то есть из точек, в которых производная равна нулю, выбрать точки экстре- мума. Нетрудно заметить, что если «подозрительная» точка от-
174 |
Раздел 3. Производная и ее приложения |
деляет промежуток возрастания функции от промежутка убыва- ния, то она обязательно будет точкой экстремума. Мы уже знаем условия возрастания и убывания функции на интервале — они связаны со знаком производной на этом интервале. Применяя их, получим следующее утверждение.
Теорема 3 (о достаточном условии экстремума).
Пусть функция у = f(x) определена на интервале (а; b) и
х0 — точка из этого промежутка.
1. Если f′(x) > 0 на интервале (а; х0) и f′(x) <0 на интервале
(х0; b), то точка х0 является точкой максимума функции. 2. Если f′(x) < 0 на интервале (а; х0) и f′(x) > 0 на интервале
(х0; b), то точка х0 является точкой минимума функции.
Часто теорему 3 формулируют так.
Если в точке х0 производная меняет свой знак, то эта точка является точкой экстремума.
Эта теорема имеет простую механическую интерпретацию. Пусть x = x(t) — закон прямолинейного движения материальной точки, где х— координата точки в момент времени t. Если x′(t) > 0
при t < t0, то это означает, что скорость точки v(t) = x′(t) положи-
тельна, и направление ее движения совпадает с направлением оси. Следовательно, координата точки возрастает при t < t0. Так как, по условию, при t > t0 v(t) = x′(t) < 0 , то точка с момента време-
ни t0 начинает двигаться в обратном направлении, ее координата убывает. Следовательно, в момент времени t0 кордината точки яв- ляется наибольшей. Аналогично можно интерпретировать второе утверждение. Таким образом, чтобы найти точки екстремума дифференцируемой функции, нужно:
1)найти производную функции;
2)найти «подозрительные» точки, то есть точки, в которых про- изводная равна нулю;
3)исследовать знак производной слева и справа от рассматри- ваемой точки;
4)опираясь на теорему 3, сделать соответствующие выводы.
Пример 4. Найти точки максимума и минимума функции f(x)= x4 – 2x3 + 5.
Функция определена и дифференцируема на всей числовой прямой. Найдем ее производную:
|
Исследование функций и построение3 |
их графиков2 2 |
с помощью производной |
175 |
|
|
|||
|
f ′(x) = 4x |
– 6x = 2x |
(2x – 3). |
|
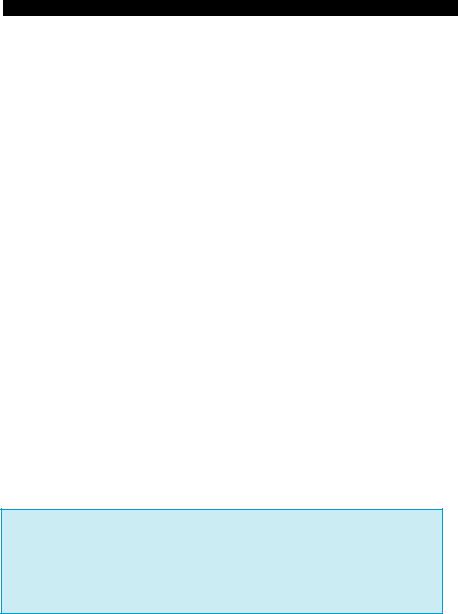
Производная равна нулю в точках х = 0 и х = 1,5, то есть эти точки «подозрительны» на экстремум. Проверим, меняет ли про- изводная знак в этих точках.
На интервалах (–∞; 0) и (0; 1,5) производная отрицательна, а на (1,5; +∞) — положительна 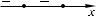 (рис. 96). То есть х = 1,5 – точка минимума фун-
(рис. 96). То есть х = 1,5 – точка минимума фун-  кции, а в точке х = 0 экстремума нет. g
кции, а в точке х = 0 экстремума нет. g 

Ответ. х = 1,5 — точка минимума функции, точек максимума нет.
 Мы находили промежутки монотонности функции
Мы находили промежутки монотонности функции
и ее точки экстремума, предполагая, что функция дифференцируема в своей области определения. Однако функции, описывающие сложные процес-
сы, могут иметь разрывы или точки, в кото- рых производная не существует. Например, на рис. 97 изображен закон движения мяча, падающего на пол и упруго отскакивающего от него (h — высота мяча над полом, t — вре-
мя). Как видим, точки t1, t2, t3, t4, t5 являются  точками минимума функции h = h(t), но про-
точками минимума функции h = h(t), но про-
изводная в этих точках не существует (эти точки являются точками излома графика).
Аналогичная картина наблюдается при нагревании чайника с водой на электроплит- ке постоянной мощности. График зависимо- сти количества теплоты в чайнике от времени
Q(t) изображен на рис. 98. Момент t0 закипа-  ния воды является точкой максимума фун-
ния воды является точкой максимума фун- 
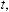
 кции, но производной в этой точке не суще-
кции, но производной в этой точке не суще- 
 ствует.
ствует.
Рассмотрим подробнее такие функции, то есть непрерывные в области определения, но
имеющие точки, в которых производная не существует. К таким функциям относится, на-
пример, функция у = |x|. Точка х = 0 являет-
ся, согласно определению, точкой минимума  функции у = |x| (рис. 99). Однако в этой точке
функции у = |x| (рис. 99). Однако в этой точке 

 производная функции не существует — точка
производная функции не существует — точка
176 |
Раздел 3. Производная и ее приложения |
О является точкой излома графика. Следовательно, функция мо- жет иметь точки экстремума не только в тех точках, где производ- ная равна нулю, но и в точках, где производная не существует.
Точки из области определения функции, в которых производная равна нулю или не существует, называ- ются критическими точками функции.
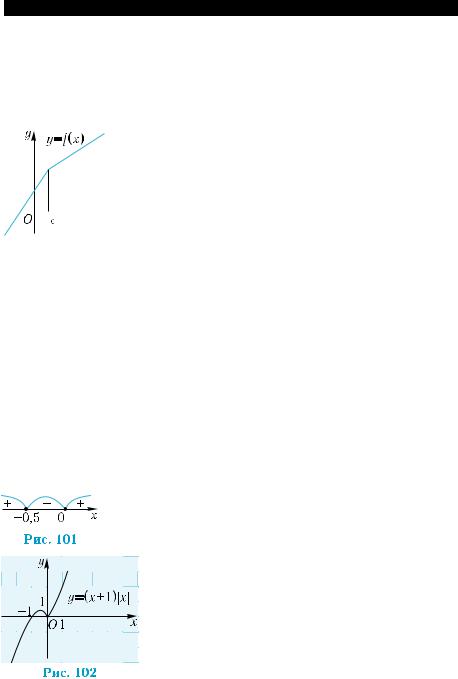
Не каждая критическая точка функции явля- ется ее точкой экстремума. В этом мы убедились, рассматривая выше функцию у = х3. Не является точкой экстремума и точка х0 для функции у = f(x), график которой изображен на рис. 100, хотя она и
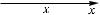 является критической точкой функции.
является критической точкой функции.
Если критические точки непрерывной фун- 


 кции удовлетворяют условиям теоремы 3, то они обязательно являются точками экстремума функции. Схема нахождения точек экстремума в этом случае
кции удовлетворяют условиям теоремы 3, то они обязательно являются точками экстремума функции. Схема нахождения точек экстремума в этом случае
аналогична схеме, приведенной выше для дифференцируемых функций. Разница заключается только в том, что в пункте 2) необ- ходимо находить не только точки, в которых производная равня- ется нулю, но и точки, в которых функция не имеет производную.
Пример 5. Найти точки экстремума функции f(x) = (x + 1)|x|.
Областью определения функции являются все действительные числа. Если х > 0, то f(x) = х2 + х и f ′(x) = 2х + 1 > 0. Если х < 0, то f(x) = –х2 – х и f ′(x) = –2х – 1. Производная функции равна нулю при
х =−12 , то есть эта точка является критической точкой функции.
|
−∞; − |
1 |
|
производная f ′(x) положи- |
|||||
На интервале |
2 |
|
|||||||
|
|
|
|
1 |
|
|
|
|
|
тельна, а на интервале |
|
;0 |
|
|
|
||||
− |
2 |
— отрицательна. |
|||||||
|
|
|
|
|
|
|
|
|
|
На рис. 101 показаны знаки производной |
|||||||||
функции. |
Отсюда |
вытекает, |
что |
точка |
|||||
х = −1 является точкой максимума фун- |
|||||||||
2 |
|
|
|
|
|
|
|
|
|
кции, а точка х = 0 — точкой минимума фун- |
|||||||||
кции. |
|
|
|
|
|
|
|
|
|

Исследование функций и построение их графиков с помощью производной |
177 |
|
|
Если построить график функции f(x) = (x + 1)|x| (рис. 102), то |
|
видно, что в точке х = 0 она не дифференцируема. g |
|
|
|
Ответ. х = −1 — точка максимума, х = 0 — точка минимума |
|
|
2 |
|
99 |
Контрольные вопросы |
|
1°. |
Укажите по графику функции y = f(x), |
|
|
изображенному на рис. 103, ее точки |
|
|
экстремума. |
|
2°. |
Может ли значение функции в точке |
|
|
максимума быть меньше, чем значение |
|
|
функции в точке минимума? |
|
3°. |
Обязательно ли точка, в которой произ- |
|
|
водная функции равна нулю, является |
|
|
точкой экстремума? |
|
4°. |
Среди каких точек следует искать точки экстремума диффе- |
|
|
ренцируемой функции? |
|
5°. |
Может ли возрастающая (убывающая) функция иметь точки |
|
|
экстремума? |
|
6°. |
Производная некоторой функции имеет вид y′ = (x − 2)(x +1)2 . |
|
|
Укажите все точки экстремума функции. Является ли точка |
|
|
х = 2 точкой максимума или минимума функции? |
|
7°. |
Какое наибольшее число точек экстремума может иметь мно- |
|
|
гочлен: а) второй степени; б) третьей сте- |
|
|
пени? |
|
8. |
Может ли точка х = 0 быть точкой экстре- |
|
|
мума нечетной функции? А четной? |
|
9. |
На рис. 104 изображен график производ- |
|
|
ной функции у = f(x). Имеет ли функция |
|
|
у = f(x) точки экстремума? Если имеет, |
|
|
то укажите, какие это точки: максимума |
|
|
или минимума? |
|
3. Построение графиков функций
Вы уже знаете, что построение графиков функций 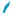
 следует начинать с ее исследования, то есть с уста-
следует начинать с ее исследования, то есть с уста-  новления основных свойств функции.
новления основных свойств функции.
Исследование функции целесообразно проводить по такой схеме.

178 |
Раздел 3. Производная и ее приложения |
1)Найти область определения функции, если она не указана.
2)Исследовать функцию на четность (нечетность). Для четных и нечетных функций можно ограничиться исследованием лишь при х ≥ 0.
3)Выяснить, будет ли функция периодической. Если функция периодическая и Т — ее основной период, то можно ограничить- ся исследованием функции на любом промежутке длиной Т.
4)Найти точки пересечения графика функции с осью х, то есть нули функции, и промежутки знакопостоянства (если это не приведет к громоздким уравнениям и неравенствам).
5)Найти промежутки возрастания и убывания функции и точ- ки экстремума функции.
6)Вычислить значения функции в точках экстремума.
7)Для уточнения графика функции можно вычислить ее зна- чения в дополнительных точках, например, найти точку пере- сечения графика с осью y.
8)Для функций, имеющих точки разрыва, необходимы допол- нительные исследования в окрестностях этих точек.
Пример 6. Построить график функции f (x) = 98 (x −1)2 (x + 1) .
1) Функция определена на всей числовой оси, то есть
D(f) = (–∞; +∞).
2) Функция не является ни четной, ни нечетной, так как, на-
пример, f(2) ≠ f(–2) и f(2) ≠ – f(–2).
3) Функция не является периодической.
4) Нулями функции являются точки х = ±1. Найдем проме- жутки знакопостоянства функции. Неравенство (х – 1)2(х + 1) > 0 выполняется при х + 1 > 0 и х ≠ 1. Следовательно, функция при- нимает положительные значения на интервалах (–1; 1) и (1; +∞).
На интервале (–∞; –1) функция принимает отрицательные значения.
На основании этих исследований уже  можно построить эскиз графика (рис. 105).
можно построить эскиз графика (рис. 105).
5) Уточним график функции с помощью производной: найдем промежутки возра-
стания и убывания, точки экстремума.
y′ = 98 (2(x − 1)(x + 1) + (x − 1)2 ) = 98 (x − 1)(2x + 2 + x − 1) = 98 (x − 1)(3x + 1) .

Исследование функций и построение их графиков с помощью производной |
179 |
|||||||||||||||||||||||||||
|
х = − |
1 |
и х = 1 — критические точки функции. |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Знаки производной показаны на рис. 106. |
на ка- |
|
|
|
||||||||||||||||||||||||
|
Следовательно, |
функция |
|
возрастает |
|
|
|
|||||||||||||||||||||
ждом из промежутков |
|
|
|
1 |
|
, [1; + ∞) и убывает на промежутке |
||||||||||||||||||||||
−∞; − |
3 |
|
||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
. Точка х |
= |
− |
— точка максимума, а точка х = 1 — точка |
||||||||||||||||||||||
− |
3 |
;1 |
3 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
минимума функции. |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
6) |
y |
|
− |
1 |
9 |
− |
1 |
−1 |
− |
1 |
+ |
1 |
|
= |
|
|
|
|
|
|
|
|
|
||||
|
|
3 |
= |
|
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= 9 16 |
|
2 |
= |
4 , у(1) = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
8 |
|
9 |
|
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7) График функции пересекает ось у в |
|
|
|
|
|
||||||||||||||||||||||
точке с координатами |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
0; |
8 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На основании дополнительных иссле- |
|
|
|
|
|
||||||||||||||||||||||
дований построим более точный график |
|
|
|
|
|
|||||||||||||||||||||||
функции (рис. 107). g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
Построим теперь график функции, имеющей точку |
||||||||||||||||||||
|
|
|
|
|
|
|
|
разрыва. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
Пример 7. Дана функция y = x3 + |
3 . |
|
||||||||||||||||||
1. Построить ее график. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|||||||||||||
2. Сколько корней имеет уравнение x3 + |
= 5 ? |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
3 = a имеет единствен- |
||||
3. При каких значениях а уравнение x3 + |
||||||||||||||||||||||||||||
ный корень? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
1. Построим график функции по указанной выше схеме. |
|
|||||||||||||||||||||||||
|
1) |
D( y) = (−∞; 0) (0; + ∞). |
|
|
|
3 |
|
|
|
|
3 |
|
|
|
3 |
|
||||||||||||
|
2) |
Так |
как |
|
|
|
|
|
3 |
+ |
|
|
= −x |
3 |
− |
|
3 |
+ |
то |
|||||||||
|
y(−x) = (−x) |
−x |
|
x |
= − x |
|
= −y(x), |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
||||
данная функция является нечетной. Поэтому ее достаточно ис- |
||||||||||||||||||||||||||||
следовать на интервале (0; + ∞). |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
180 |
Раздел 3. Производная и ее приложения |
|||||||
3) Функция является непериодической. |
|
|
|
|
|
|||
4) С осью абсцисс график функции не пересекается, так как |
||||||||
уравнение x3 + |
3 = 0 корней не имеет. Если х > 0, то у > 0, то есть |
|||||||
|
x |
|
|
|
|
|
|
|
функция принимает положительные значения при х > 0. |
||||||||
Исследуем функцию с помощью производной. |
3(x4 −1) |
|
||||||
|
5) Так как y′ = 3x |
2 |
3 |
|
, то кри- |
|||
|
|
− x2 , или |
y′ = |
|
x2 |
|
||
тическими точками функции являются точки х1 = –1, |
||||||||
х2 |
= 1. Знаки производной для |
х > 0 изображены на |
||||||
рис. 108. |
|
|
|
|
|
|
|
|
Напромежутке(0;1]функцияубывает,анапромежутке[1; +∞) — |
||||||||
возрастает. Точка х = 1 является точкой минимума функции. |
||||||||
6) у(1) = 4. |
|
|
|
|
|
|
|
|
7) График не пересекает ось у, так как в точке х = 0 функция не |
||||||||
определена. |
|
|
|
|
|
|
|
|
8) Функция непрерывна на промежутках (–∞; 0) и (0; +∞). Точ- |
||||||||
ка х = 0 является точкой разрыва функции. Исследуем поведение |
||||||||
функции в окрестности этой точки. Если значения аргумента х |
||||||||
приближаются к нулю справа, то первое слагаемое |
х3 стремится к |
|||||||
нулю, а второе — становится как угодно большим (проверьте это |
||||||||
|
|
|
утверждение, положив х = 0,1; |
|||||
|
|
|
0,01; 0,001 и т. д.). График |
|||||
|
|
|
функции приближается к оси |
|||||
|
|
|
у как угодно близко, но не пе- |
|||||
|
|
|
ресекает ее, так как при х = 0 |
|||||
|
|
|
функция не определена. Ось у |
|||||
|
|
|
является вертикальной асим- |
|||||
|
|
|
птотой графика функции. |
|||||
|
|
|
Построим график функции |
|||||
|
|
|
на промежутке (0; +∞). Так как |
|||||
|
|
|
функция |
является |
нечетной, |
|||
|
|
|
то ее график симметричен от- |
|||||
|
|
|
носительно начала координат |
|||||
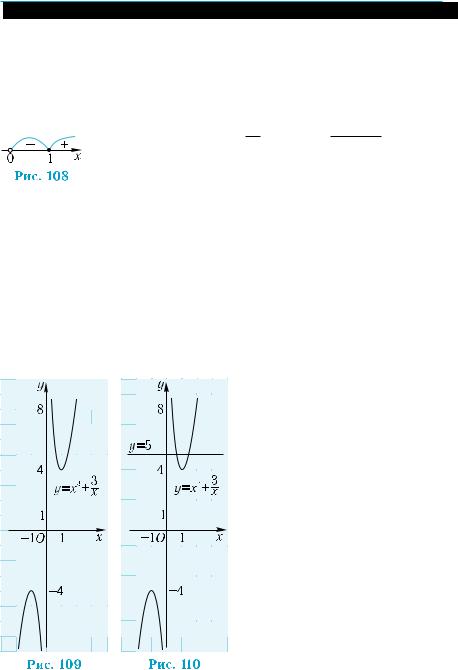
|
|
|
(рис. 109). |
|
|
|
|
|
|
|
|
2. Прямая у = 5 пересекает |
|||||
|
|
|
график функции в двух точ- |
|||||
|
|
|
ках. Следовательно, уравне- |
|||||
|
|
|
ние имеет два корня (рис. 110). |
|||||

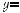
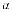
 сказанному выше, имеет не более одно
сказанному выше, имеет не более одно
