
978-966-10-2413-6_Matematuka 11_rus
.pdf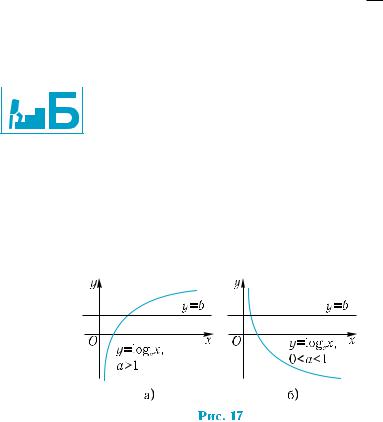
Решение показательных и логарифмических уравнений, неравенств |
|
|
|
|
51 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
Сколько корней имеет уравнение: |
а) |
2 |
x |
= |
1 |
; |
1 |
x |
|
|
1 |
; |
|
||
|
x |
б) |
= − |
x |
|
|||||||||||
|
|
в) 2x = −x ? |
|
|
|
|
|
|
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
При каких значениях а уравнение |
|
1 x |
= 1 − a имеет корни? |
||||||||||||
|
|
|||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
5. |
Каково решение неравенства: а) 2 |
x |
> 0; |
|
|
|
1 x |
< 0; |
в)2 |
x |
>1; |
|
||||
|
|
б) |
2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
г) 2x <1; д) 2x > −1?
6.Какие целые числа удовлетворяют неравенству: а) 271 < 3x < 3;
б) |
1 |
1 |
x |
? |
||
9 |
≤ |
3 |
|
≤ 9 |
||
|
|
|
|
|
||
2. Логарифмические уравнения и неравенства
 Логарифмические уравнения и неравенства — это
Логарифмические уравнения и неравенства — это
 такие уравнения и неравенства, в которых неиз- вестные содержатся под знаком логарифма. Про- стейшее логарифмическое уравнение имеет вид loga x = b . Его
такие уравнения и неравенства, в которых неиз- вестные содержатся под знаком логарифма. Про- стейшее логарифмическое уравнение имеет вид loga x = b . Его
решение найти нетрудно. Например, уравнению log3 x = 2 удов- летворяет число х = 32 = 9, так как log3 9 = 2 . Понятно, что уравне- ние loga x = b имеет решение при любом b R.
Так как функция y = loga x монотонна, то каждое свое значе-
ние она принимает лишь в одной точке, то есть прямая у = b, b R, пересекает ее график лишь в одной точке (рис. 17).
Таким образом, уравнение loga x = b имеет единственное ре-
шение, которое, согласно определению логарифма, имеет вид x = ab.

52 |
|
Раздел 1. Показательная и логарифмическая функции |
||
Пример 10. Решить уравнение: |
|
|
||
1) log5(2 – x) = 2; |
2) log3(x2 – x + 11) = 2. |
|||
|
1) По определению логарифма, 52 |
= 2 – х, откуда х = – 23. |
||
2) |
Данному |
уравнению, согласно |
определению логарифма, |
|
удовлетворяют те значения х, для которых выполняется равенст-
во x2 − 3x + 11 = 32 . Полученное квадратное уравнение имеет кор- нями числа х1 = 1 и х2 = 2, которые являются решениями данного
уравнения. g
Ответ. 1) – 23; 2) 1 и 2.
Рассмотрим логарифмические уравнения вида loga f (x) = loga g(x) .
Пример 11. Решить уравнение log2(х – 2) = log2(x2 – x – 17).
Если х0 — корень этого уравнения, то имеет место числовое ра венство log2 (x0 − 2) = log2 (x02 − x0 − 17), поэтому x0 − 2 = x02 − x0 −17 (последнее равенство следует из монотонности логарифмической функции). Отсюда: x02 − 2x0 −15 = 0. Это равенство верно, если
х0 = 5 или х0 = –3. Итак, предположив, что число х0 — корень дан- ного уравнения, мы показали, что оно может равняться или 5, или –3. Проверим, являются ли эти числа корнями исходного уравнения. Подставляя последовательно в его левую и правую
части число 5, |
получим: |
log2 (x − 2) = log2 (5 − 2) = log2 3; |
|
log2 (x2 − x −17) = log2 |
(25 − 5 |
−17) |
= log2 3, то есть х = 5 — корень |
данного уравнения. При х |
= – 3 значения выражений x − 2 и |
||
x2 − x −17 отрицательны, обе части уравнения не имеют смысла, то есть х = –3 не является корнем данного уравнения. g
Ответ. 5.
Рассмотренный пример показывает, что
!при переходе от уравнения logaf(x)= logag(x) к уравнению f(x)= g(x) могут появиться посторонние корни. Поэ-
тому необходимо выполнить проверку.
Решение логарифмических неравенств основано на использо- вании монотонности логарифмических функций. Функции y = loga x определены при х > 0 и при а > 1 возрастающие, а при
0 < a <1 — убывающие.
Пример 12. Решить неравенство: 1) log3x < –1; 2) log1 |
x ≤ −2 . |
3 |
|

Решение показательных и логарифмических уравнений, неравенств |
53 |
|
|
|
|
|
||||||||
|
1) Запишем |
неравенство |
в виде |
log3 x < log3 3−1 , или |
||||||||
log |
3 |
x < log |
3 |
1 . |
Функция y = log |
3 |
x |
определена при х > 0 и являет- |
||||
|
|
|
3 |
|
|
|
|
|
|
|||
ся возрастающей (основание логарифма больше 1), поэтому нера- |
||||||||||||
венство выполняется при х > 0 и x < 1 , то есть при 0 < x < |
1 . |
|||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
3 |
|
2) Неравенство |
log1 x ≤ −2 |
можно |
записать в |
виде |
|||||||
|
|
|
|
|
|
−2 |
3 |
|
|
|
|
|
log1 |
|
|
1 |
|
|
|
|
|
опреде- |
|||
x ≤ log1 |
, или log1 x £log1 9 . Функция y = log1 x |
|||||||||||
|
|
3 |
|
3 |
3 |
|
3 |
|
|
3 |
3 |
|
лена при х |
> 0 и является убывающей (так как основание лога- |
|||||||||||
рифма находится между 0 и 1), поэтому неравенство выполняется при х > 0 и х ≥ 9, то есть при х ≥ 9. g
Ответ. 1) 0 < x < 13 ; 2) х ≥ 9.
Логарифмические неравенства вида log f(x)< log g(x) можно ре- шать по такой схеме: a > a
1)записать условия, задающие область определения неравен- ства, то есть указать множество значений переменной, при ко- торых имеют смысл выражения, входящие в неравенство;
2)отбросить знаки логарифмов с учетом возрастания или убы- вания логарифмической функции;
3)решить полученное неравенство;
4)записать ответ с учетом области определения неравенства.
Пример 13. Решить неравенство lg(3x – 4) < lg(2x + 1).
Будем действовать по приведенной схеме.
1) Логарифмическая функция у = lg x определена при x > 0, потому неравенство имеет смысл при 3х – 4 > 0 и 2 x + 1 > 0, или
при x > |
4 |
и x > − |
1 |
. Следовательно, его областью определения |
|
|
3 |
|
2 |
4 |
|
|
|
|
|
||
является промежуток |
; +∞ . |
||||
|
|
|
|
3 |
|
2) Так как логарифмическая функция с основанием 10 явля-
ется возрастающей, то, отбросив знаки логарифмов, получим:
3х – 4 < 2x + 1.
3) Решим полученное неравенство: х < 5.

54 |
|
Раздел 1. Показательная и логарифмическая функции |
|||
|
|
|
|
|
|
|
4) С учетом области определения имеем: |
4 < x < 5. g |
|||
|
4 |
|
3 |
|
|
|
|
|
|||
|
Ответ. |
;5 |
|
|
|
|
3 |
|
|
|
|
|
|
|
При решении логарифмических уравнений приме- |
||
|
|
|
|||
|
|
|
няют: |
|
|
|
|
|
— переход от уравнения |
loga f (x) = loga g(x) к |
|
|
|
|
уравнению f (x) = g(x) ; |
|
|
|
|
|
|
|
|
— свойства логарифмов;
— замену переменной;
— разложение на множители;
— логарифмирование;
— функциональные методы.
Проиллюстрируем эти методы на конкретных примерах. При решении логарифмических уравнений часто приходится
выполнять преобразования, применяя свойства логарифмов. При этом может нарушиться равносильность уравнений.
Пример 14. Решить уравнение lg(x + 2) + lg(x – 2) = lg5.
Согласно свойству логарифма произведения (см. § 2), имеем: lg((x – 2)(x + 2))= lg5. Отсюда следует, что х2 – 4 = 5. Корнями этого уравнения являются числа 3 и –3. Нетрудно проверить, что оба числа являются корнями уравнения lg(х2 – 4)= lg5, но только чи- сло 3 является корнем исходного уравнения.
Посторонний корень появился после выполнения преобразова- ния lg(x + 2) + lg(x − 2) = lg(x2 − 4) , в результате которого получи-
ли уравнение с более широкой областью определения. Действи- тельно, выражения, содержащиеся в данном уравнении, имеют смысл при х (2; +∞), а в полученном — при х (–∞; –2) (2; +∞). Расширение области определения уравнения привело к появле- нию посторонних корней. g
Ответ. 3.
!При решении данного уравнения мы переходили от суммы логарифмов к логарифму произведения. При этом переходе, а также при переходе от разности логарифмов к логарифму частного, от произведения четного числа на логарифм некоторого выражения к логарифму степени могут появиться посторонние корни и потому проверка необходима. Если же переходить от логарифма произве-

Решение показательных и логарифмических уравнений, неравенств |
55 |
дения, частного или же четной степени к сумме, разности логарифмов или же к произведению четного числа на логарифм, можно потерять корни.
Распространенным является метод сведения логарифмических уравнений к более простым (например, алгебраическим) введени- ем новых неизвестных.
Пример 15. Решить уравнение log22 x − 2log2 x − 3 = 0 . |
||||||
Обозначив log2x = у, |
получим |
|
квадратное уравнение |
|||
y2 − 2y − 3 = 0 , имеющее корни y |
= 3, y |
|
= −1. Решение задачи |
|||
|
|
|
1 |
2 |
|
|
свелось к двум простейшим уравнениям |
log2 x = 3 и log2x = –1, из |
|||||
которых находим: x = 23 = 8, x |
2 |
= 2−1 = 0,5. g |
||||
Ответ. 8; 0,5. |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Пример 16. Решить уравнение |
x lg(x −1) = 0 . |
|||||
Левая часть уравнения является произведением двух мно- жителей. Приравняем каждый из них нулю и решим полученные
уравнения: x = 0 , х = 0; lg(х – 1)= 0, х – 1 = 1, х = 2. Легко заметить, что число х = 0 не является корнем исходного уравнения, так как при х = 0 выражение lg(х – 1) не имеет смысла. В то же время чис ло х = 2 является корнем данного уравнения. g
Ответ. 2.
!При решении логарифмического уравнения вида f(x)logag(x) = 0 сведением к уравнениямf(x)= 0 и logag(x) = 0
необходимо проверить, удовлетворяют ли их корни ис-
ходному уравнению.
Если неизвестная под знаком логарифма стоит в показателе степени, то иногда целесообразно прологарифмировать обе части равенства: ведь уравнение f (x) = g(x) равносильно уравнению
loga f (x) = loga g(x) при условии, что f(x) > 0 и g(x) > 0. Пример 17. Решить уравнение 73 lg x = 34,3x .
Обе части уравнения принимают положительные значения: левая часть как степень некоторого числа, правая часть – на осно-
вании того, что х > 0. Учитывая, что 34,3 = 34310 = 1073 , прологариф-
мируем обе части уравнения по основанию 10: 3lg x lg7 = 3lg7 −
− lg10 + lg x . Отсюда: lg x(3 lg 7 −1) = 3 lg 7 −1, lg x = 1,x = 10. g
Ответ. 10.
56 |
Раздел 1. Показательная и логарифмическая функции |
Как и для показательных уравнений, при решении логариф- |
|
мических уравнений часто оказывается полезным применение |
|
свойств и графиков функций, входящих в уравнение. |
|
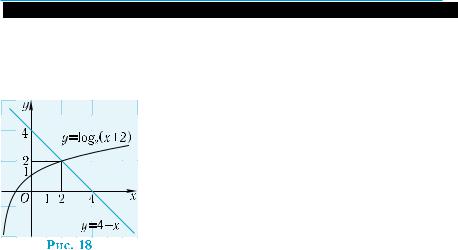
Пример 18. |
Решить уравнение log2 (x + 2) = 4 − x. |
|
Ни одним из рассмотренных в предыду- |
|
щих примерах методов решить это уравнение |
|
не удаётся. Попробуем найти какое-нибудь |
|
его решение подбором. В данном случае это |
|
сделать нетрудно: х = 2, ибо log2 (2 + 2) = 2, |
|
4 – 2 = 2. Покажем, что других корней уравне- |
|
ние не имеет. Функция y = log2 (x + 2) являет- |
|
ся возрастающей, а функция y = 4 − x — убы- |
|
вающей(рис.18).Поэтомупри x > 2 значения |
|
первой функции больше 2, а второй — мень- |
ше 2; при х < 2, наоборот, значения первой функции меньше 2, а |
|
второй — больше 2. Поэтому графики этих функций не могут иметь |
|
точек пересечения прих ≠ 2. g |
|
Ответ. 2. |
|
Решение логарифмических неравенств основано на использо- |
|
вании монотонности логарифмических функций и учете области |
|
ее определения, то есть на следующей теореме, вытекающей из |
|
свойств логарифмической функции. |
|
Теорема. Неравенство loga f (x) < loga g(x) при a > 1 рав
носильно системе |
f (x) < g(x), |
а при 0 < a < 1 — системе |
|
||
|
f (x) > 0, |
|
Решить неравенство:
1)log2 (1 − 4x) > log2 (x2 + 4); 2) log1 (x − 2) > −3.
1)Вданномслучаеоснование3логарифмабольше1,поэтомудан
|
|
1 − 4x > x |
2 |
+ 4, |
|
ное неравенство равносильно системе неравенств |
|
|
|
||
|
4 > 0 |
|
|
||
|
|
x2 + |
|
|
|
|
|
|
|
|
|
или неравенству |
x2 + 4x + 3 < 0, так как неравенство |
x2 + 4 > 0 |
|||
выполняется при |
всех значениях х. Решением неравенства |
||||

Решение показательных и логарифмических уравнений, неравенств |
57 |
x2 + 4x + 3 < 0 является промежуток, содержащийся между корня-
ми –3 и –1 уравнения |
x2 |
+ 4x + 3 = 0 . Следовательно, решением |
||
данного неравенства является интервал (–3; –1). |
||||
2) Представим –3 как log1 27, |
тогда данное неравенство при- |
|||
|
|
|
3 |
|
нимает вид: log1 (x − 2) > log1 27. |
Так как основание логарифма |
|||
3 |
|
|
3 |
|
находится между 0 и 1, то последнее неравенство равносильно |
||||
двойному неравенству |
0 < x − 2 < 27 . Решая систему двух линей- |
|||
x − 2 < 27, |
получим: 2 < x < 29. g |
|||
ных неравенств |
|
|
||
x − 2 > 0, |
|
|
|
|
Ответ. 1) (– 3; –1); 2) (2; 29). |
|
|||
99 |
Контрольные вопросы |
|
|
|
|
||
1°. |
Может ли уравнение loga x = b не иметь решений? |
|
|||||
2°. |
Может ли уравнение loga x = b иметь отрицательное решение? |
||||||
3°. |
Может ли уравнение loga x = b иметь два решения? |
|
|||||
4°. |
Каково решение уравнения: |
|
|
|
|
||
|
а) log2 x = 0; |
б) log1 x = −1; |
в) logx 3 = 2? |
||||
5. |
|
2 |
|
|
|
|
|
Сколько решений имеет уравнение: |
|
|
|
||||
|
а) log2 x = 1 ; |
б) log1 x = − 1 ; |
в) log2 x = −x ? |
||||
|
x |
2 |
x |
|
|
|
|
6. |
Верно ли решено уравнение log2 x2 |
= log2 9 , |
2 log2 x = 2 log2 3, = |
||||
|
х = 3? |
|
|
|
|
|
|
7. |
Каково решение неравенства: |
|
|
|
|
||
|
а) log2 x < 0; б) log1 x > 0; |
в)log3 x <1; |
г) log1 x > −1? |
||||
8. |
|
2 |
|
|
|
3 |
|
Какие целые числа удовлетворяют неравенству: |
|
||||||
|
а) 2 < log2 x < 3; |
|
б)−2 ≤ log1 x ≤ −1 ? |
|
|||
9*. Имеет ли решения уравнение: |
|
2 |
|
|
|||
б) lg(x |
– 1) + lg(1 –х) = 0? |
||||||
|
а) ln x − ln(x + 2) = 2; |
|
|||||

58 Раздел 1. Показательная и логарифмическая функции
Задачи
49. |
Решите уравнение: |
|
|
|
|
|
|
|
|
|
|
|
|
x2 −3x −3 |
|
|
|
|
|||||||||||
|
1°) |
4 |
x2 |
−3x −4 |
= 1; |
|
2°) 64 |
x |
= |
4 |
x2 |
+2 |
; |
3°) |
1 |
|
1 |
; |
|||||||||||
|
|
|
|
|
|
|
|
|
|
= |
5 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|||
|
4°) |
4 |
x2 |
−x +1 |
= 8 |
x |
; |
|
5) 2 |
x +1 |
5 |
x |
= 200; |
6*) |
4 |
x −2 |
= |
|
1 x |
||||||||||
|
|
|
|
|
|
|
|
4 |
2 |
. |
|||||||||||||||||||
50. |
Решите уравнение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
2°) 5–2х = 4–х; |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
1°) 3х = 2 х; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
3) 3−x +4 − 25 52− x = 0; |
|
|
|
|
|
4) 81 · 8х – 3 – 9х – 1 = 0. |
|
|
|
|
|
|||||||||||||||||
51. |
Решите уравнение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
1°) 22х – 2х – 12 = 0; |
2°) 16х – 4х – 2 = 0; |
3) 3x + 31−x |
= 4; |
|
|
|
||||||||||||||||||||||
|
4) 32x +1 + 10 3 x +3 = 0; 5) 2 9x − 5 6x − 3 4x = 0 . |
|
|
|
|
|
|
|
|||||||||||||||||||||
52°.Решите уравнение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
1) 5x +1 − 5x −1 = 24; |
|
|
|
|
|
2) 23x 3x |
− 23x −1 3x +1 + 288 = 0; |
|||||||||||||||||||||
|
3) |
|
x +3 |
|
2x +2 |
|
82 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
9 |
|
|
+ 3 |
|
|
= 9 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
53. |
Найдите наименьший корень уравнения: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
1) (9x2 −1 − 1) 2x − 1 = 0; |
|
|
|
|
2) (4x +2 − 2x ) 1 + x = 0. |
|
|
|
|
|||||||||||||||||||
54. Найдите точки пересечения с осью абсцисс графика функции: 1) у = 3х – 1 – 6х ·2- х ·3х + 1; 2) y = 4sin x cos x − 2 ;
3) у = 2х + 2х – 1 + 2х – 2 – 3х + 3х – 1 – 3х – 2.
55.Найдите точки пересечения графиков функций:
|
1) y = 3x −1 23x −7 и у = 129 – х; |
|
2) y = 9x +1 + 92x −1 иy = 54 27x −1 ; |
||||||||||||||
|
3) y = 3 4x + 2 9x и y = 5 6x ; 4) y = 4x и y = 24 − 2x +1. |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
56. |
Решите неравенство: |
|
2x −1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
|
1 |
−3 |
|
|
|
|
|
|
||||
|
1°) 23−6x > 1; |
2°) |
1− x |
> |
|
|
|
|
|
|
|||||||
|
|
|
; 3) x +1 3 > 9; |
||||||||||||||
|
|
|
|
5 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
4) 3x > 2; |
5°) |
2x2 −6x −2,5 > 16 |
2. |
|
|
|
|
|
|
|||||||
57. |
Решите неравенство: |
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|||
|
1) 52x + 1 > 5x + 4; |
|
|
|
2) |
|
|
|
|
> |
|
; |
|||||
|
|
|
|
|
2x + 3 |
|
2x +3 + 1 |
||||||||||
|
3) 22x + 2 + 6x – 2 · 32x + 2 > 0; |
|
4) 3x + 1 |
– 5 |
· 2x ≤ |
2x + 2 – 3x. |
|||||||||||

Решение показательных и логарифмических уравнений, неравенств |
59 |
58. |
Решите систему уравнений: |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
x |
+ 3 |
y |
= 7, |
|
|
|
x |
− 36y = 0, |
|
||||
|
1) |
2 |
|
|
|
2) |
5 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
− 25y = 0; |
|
|||||
|
|
22x + 32 y = 25; |
|
6x |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= 10y, |
|
|
||
|
|
2 |
x |
+ 2 |
y |
= 12, |
|
|
|
x |
|
|
|||||
|
3) |
|
|
|
4) |
8 |
|
|
|
||||||||
|
|
x + y = 5; |
|
|
= 5y. |
|
|
||||||||||
|
|
|
|
2x |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
59. |
Дана функция y = f (x), где |
f (x) |
1 |
x +1 |
1 |
2− x |
|||||||||||
= |
|
|
− |
. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
3 |
|
пересекается с |
||
|
1°) В каких точках график функции y = f (x) |
||||||||||||||||
осями координат?
2)Решите уравнение f (x) = − 92 .
3)Решите неравенство f (x) < − 92 .
4) Найдите область определения функции y = f (x).
60.Культуре из 100 бактерий предоставлена возможность раз- множаться в благоприятных условиях по закону N = N0ekt, где N — число бактерий в момент t, N0 — количество бактерий в начальный момент времени t = 0, k — некоторая константа. Через 12 ч оказывается, что культура содержит 500 бактерий. Сколько бактерий будет через 2 суток после начала опыта?
61.Закон радиоактивного распада вещества имеет вид m = m0 2− Tt , где m0 — масса вещества в начальный момент t = 0, m — масса вещества в момент t, T — некоторая константа, которую назы- вают периодом полураспада. Через время T после начального момента масса радиоактивного вещества уменьшается вдвое. Вычислите период полураспада вещества, если за год ее мас- са уменьшилась в десять раз.
62.Решите уравнение:
1°) |
log1 (2x2 + 3x +1) = 0; |
2°) |
log2 (x − 7) = log2 (4 − x); |
3°) |
4 |
4°) |
log2 (x − 2) = log2 (x2 − x −17); |
log3 x − 2log1 x = 6; |
|||
|
3 |
|
|
5) log5 log4 log3 x = 0; |
6) log5−x (x2 − 2x + 65) = 2. |
||

60 |
|
|
|
|
|
Раздел 1. Показательная и логарифмическая функции |
|||||||||||||||
63°.Решите уравнение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1) |
log3 (x + 1) + log3 (x + 3) = 1; |
2) lg2x = 4 – 3lgx; |
|
|
|
|||||||||||||||
|
3) |
6 logx 2 − 6 log4 x + 7 = 0; |
4) |
|
1 |
|
|
+ |
|
|
1 |
= 1. |
|
||||||||
|
3 − lg x |
1 + lg x |
|
||||||||||||||||||
64. |
Решите уравнение: |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1°) 100lg( x +20) |
= 1000; |
2°) 54 lg x = 62,5x; |
|
|
|
|||||||||||||||
|
3) |
xlg x +2 |
= 1000; |
|
4*) xlg x2 −3 |
= 100. |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
||
65*.Найдите наименьший корень уравнения |
|
|
|
|
|
|
|
|
|||||||||||||
|
1) (x2lg x − 10x) 3x − 2 = 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2) |
(log2 (9 − 2x ) − 3 + x) 2x − 3 = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
66. |
Найдите точки пересечения графиков функций: |
|
|
|
|||||||||||||||||
|
1) y = x(1 − lg 5) и y = lg(4x −12); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2) * y = log2 |
|
x2 + 2x + 1 и y = 6 − log2 (x + 1)2 ; |
|
|
|
|
|
|
||||||||||||
|
3) y = lg(35 − x3 ) и y = 3lg(5 − x); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
4) |
y = 4 − lg x и y = 3 lg x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
67. |
Решите графически уравнение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1) |
log2 x = −x + 1; |
2) log1 x = 4x2 . |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Решите неравенство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
68. |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1°) log5 (3x −1) < 1; |
2°) log2 (x2 − 2x) − 3 > 0; |
|||||||||||||||||||
|
3) |
(log2 x)2 ≤ 4; |
|
|
4) |
|
1 |
|
|
|
|
|
≤ |
1 . |
|
|
|
||||
|
|
|
log2 (x − 2) |
|
|
|
|||||||||||||||
69. |
Решите неравенство: |
|
|
|
2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1) lg(x2 – 3) > lg(x + 3); |
2°) lg2 x − 2lg x − 8 ≤ 0; |
|||||||||||||||||||
|
3) |
x2 + 4x |
< 1; |
|
4) |
|
1 log19 |
( x2 −3x +1) |
< 1 . |
|
|
||||||||||
|
log1 |
2x − 3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
70. |
|
3 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||
Решите систему уравнений: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1°) |
lg x − lg y = 7, |
2°) |
|
lg x − lg y = 2, |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
lg x + lg y = 5; |
|
|
x −10y = 900; |
3 |
|
|
|||||||||||||
|
|
lg x + lg y = 4, |
|
|
|
+ log9 |
y = |
, |
|
||||||||||||
|
3) |
4) |
log3 x |
2 |
|
||||||||||||||||
|
|
= 1000; |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
xlg y |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
logx 3 + log y 9 = 3. |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
