
978-966-10-2413-6_Matematuka 11_rus
.pdf
Логарифмы и их применение |
41 |
9.При каких значениях х имеет смысл выражение:
а) x ln 0,5; |
б) 1 − log2 x; |
в*) |
x |
? |
|
ln x |
|||||
|
|
|
|
10*.При каких значениях а функция y = log3a +1 x является убыва-
ющей?
11. График какой функции получим, если график функции y = log0,5 x параллельно перенесем на две единицы в положи-
тельном направлении оси х?
Задачи
20°.Вычислите: |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||||
1) |
log |
|
16; |
2) log |
|
1; |
|
|
|
3) log |
|
; |
|
|
||||
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
2 |
8 |
|
|
2 |
|
5) |
|
|
|
6) log1 |
|
|
1 |
|
|
7) log1 |
|
1 |
||||||
log1 |
9; |
|
|
|
|
|
; |
|
|
|
; |
|||||||
27 |
3 |
|||||||||||||||||
|
|
3 |
|
3 |
|
|
3 |
|
|
|
||||||||
9) |
log1 |
3 3; |
10) log1 |
3 3 |
. |
|
|
|
|
|
||||||||
|
|
9 |
|
|
|
|
|
|||||||||||
|
|
3 |
|
|
3 |
|
|
|
|
|
|
|
|
|||||
21°.Заполните пустые клетки таблицы. |
|
|
|
|
|
|||||||||||||
4) log2 3 4;
8 ) log1 |
4 27; |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
logab |
|
|
–4 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
–5 |
|
–2 |
|
0,5 |
3 |
|
|
|
|
|
|
|
|
||||||
a |
|
|
2 |
|
|
|
|
|
|
3 |
5 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
9 |
|
|
0,1 |
|
|
е |
||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
b |
|
|
|
|
|
|
|
|
|
|
|
0,04 |
|
27 |
|
|
1 |
|
81 |
|
|
|
|
8 |
|
100 |
|
|
1 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
32 |
|
|
|
|
|
|
|
|
e2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
22°.Найдите значение выражения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
1) 3log3 12 ; |
|
|
|
|
|
|
|
2) 10lg 3 ; |
|
|
|
|
|
|
|
3) eln 5 ; |
|
|
|
|
|
|
|
|
||||||||||||||
4) (0,2) |
log1 |
7 |
; |
|
|
|
|
5) |
|
1 log0,25 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
5 |
|
|
|
|
|
|
4 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
23°.Вычислите: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
3log |
1 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,25log |
1 16 |
|
|||||||||||||||
1) |
|
|
|
|
; |
|
|
|
|
|
2) |
1 |
|
|
|
|
3) 5 |
1 |
log5 |
7 |
; |
|
|
4) |
|
1 |
|
|||||||||||
|
5log |
2 |
|
|
|
|
|
|
|
2 |
; |
|
|
|
|
|
|
|
3 |
. |
||||||||||||||||||
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
24. Вычислите: |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
log4 3 |
|
|
|
||||||||||||
|
|
|
|
|
|
log |
|
|
1 |
|
|
|
log |
12 |
|
|
|
|
|
|
|
|
log3 |
5 |
|
|
|
1 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
1) |
0,125 |
|
|
0,5 |
|
; |
2) |
9 |
|
3 |
|
; |
|
|
|
|
3) ( |
|
3) |
|
|
|
; |
4) |
|
|
|
|
|
. |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

42 Раздел 1. Показательная и логарифмическая функции
25. |
Найдите х, если: |
|
|
1 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1) |
log 3 = 2 ; |
2) log 5 = |
|
3) log |
|
7 = 2 ; |
|
4) |
log 6 = 4 . |
||||||||||||||||
|
|
x |
|
|
|
|
|
|
x |
|
2 |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
26°.Решите уравнение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1) |
log6 x = 3; |
|
|
|
|
|
|
2) log2 (5 − x) = 3; |
|
|
|
|
|
||||||||||||
|
3) |
log3 (x + 2) = 3; |
|
|
|
|
4) log1 |
|
|
1 |
|
= −2. |
|
|
|
|
||||||||||
|
|
|
|
|
x − |
2 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
27. |
Найдите значение выражения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1°) log3 2,7 + log3 10; |
2°) lg12 − lg1,2; |
|
|
3°) loga a5 ; |
|
||||||||||||||||||||
|
4) |
log0,5 |
|
1 |
|
3 |
|
5) log0,5 |
12,5 |
; |
|
|
6°) loga |
4 |
a |
3 |
. |
|||||||||
|
|
8 |
|
2 ; |
100 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
28. |
Вычислите: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
|
|
|
||||||
|
|
lg 25 |
|
|
|
|
|
|
|
log5 27 |
|
|
|
|
|
|
|
log7 |
|
|
|
|||||
|
1) |
; |
|
|
|
|
|
2) |
; |
|
|
|
3) |
|
4 |
|
; |
|
||||||||
|
lg 5 |
|
|
|
|
|
log5 |
3 |
|
|
|
|
log7 2,5 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
4)(log 2 5)(log5 2); 5) log 3 2 + log3 2,25.
29.Вычислите с помощью калькулятора с точностью до 0,001: 1°) lg 17; 2°) lg 127; 3°) ln 2,9;
4°) ln 0,72; 5) log342; 6) log0,256,2.
30.Найдите с точностью до 0,001 решение уравнения:
1) |
2x = 5; |
2) 1,2x |
= 4; |
3) 1 + e0,2x = 5; |
||
4) |
23x −1 = 5; |
5) |
4 |
2 |
= 1,3; |
6) 3x2 −2 = 2. |
3x |
||||||
31.Упростите данное выражение и вычислите с точностью до 0,001 с помощью калькулятора его значение при х = 1,21:
1) |
2lg100x4 −3lg |
x |
; |
2) |
log3 x + log3 27x2 ; |
|||
10 |
||||||||
|
0,5ln x3 + 2ln x |
|
|
|
|
|
||
3) |
− ln(e2 x). |
|
|
|
||||
|
e |
|
|
|
|
|
|
|
32°. |
|
|
|
|
|
x |
. |
|
|
|
|
|
100 |
||||
1) |
Докажите, что f(x) = 10 + 7lg x. |
|
||||||
|
|
|
||||||
2) |
Вычислите значение выражения при х = 0,01; 1,2. |
|||||||
3) |
При каком значении |
х справедливо равенство f(x) = 3? |
||||||
Логарифмы и их применение |
43 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
33.Скорость погружения тела в жидкость описывается с помо-
щью формулы v = 2,5(1 − 2,7−1,5 t ), где v — скорость, м/с; t — время, с.
1)Через сколько секунд после начала погружения скорость будет равняться 2,2 м/с?
2*) Через сколько секунд скорость тела будет составлять 95% от числа, к которому приближается значение данной фун- кции при стремлении t к бесконечности?
34.Конструкция вакуумного насоса рассчитана на откачивание за один ход поршня из камеры 3% газа от того количества, ко- торое было в камере перед этим ходом поршня. Сколько таких ходов нужно сделать, чтобы откачать из камеры 99% газа?
35.Количество особей биологической популяции в течение ка- ждой единицы времени увеличивается на 8 % по отношению к предыдущей единице времени. Через сколько единиц вре- мени численность популяции удвоится?
36.Давление воздуха падает с ростом высоты (при постоянной
температуре) по закону p = p0e− Hh , где р0 — давление на уров- не моря (h = 0), p – давление на высоте h, H — некоторая кон- станта, зависящая от высоты. Найдите формулу для вычисле- ния высоты в зависимости от давления.
37.Найдите область определения функции у = f(x):
|
1°) f (x) = log3 (x + 3); |
|
2°) f (x) = lg(x2 +1); |
|
|||||||||||||
|
3°) f (x) = log0,3 (1 − x2 ); |
4) |
f (x) = lg (2x −1); |
|
|||||||||||||
|
5) |
f (x) = |
log0,5 x ; |
|
6*) f (x) = alog2 x ; |
|
|
|
|
|
|||||||
|
7) |
f (x) = lg lg x. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
38°.Определите знак числа: |
|
|
|
|
|
|
|
|
|
|
|||||||
39. |
1) log53; |
|
2) log30,9; |
3) log0,78; |
|
4) log0,30,6. |
|||||||||||
Сравните числа: |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1) |
log |
|
9 |
и log |
10 ; |
|
2) |
log |
3 |
7 |
и log |
3 |
2,6 ; |
|
||
|
5 10 |
|
|
||||||||||||||
|
|
|
|
5 11 |
|
|
|
|
|
|
|
|
|
||||
|
3) |
log0,2 4,21 и log0,2 4,19 ; |
4) |
log0,9 |
e |
и log0,9 p. |
|
||||||||||
40. |
Расположите числа |
а, b, c по возрастанию: |
|
|
5π |
|
|
||||||||||
|
1)a = 2−0,5 ; b = 2cos π |
; c = log0,1 2; |
|
2)a = 10 1,1; b = ctg |
|
; c = log2 5. |
|||||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
4 |
|
|
|

44 Раздел 1. Показательная и логарифмическая функции
41. |
Решите неравенство: |
|
|
|
1 ; |
|
|
|
|
|
||||
|
1°) log5 x > log5 3; |
|
2°) log1 x £log1 |
|
3) log3 x < log3 2; |
|||||||||
|
|
1 ; |
|
|
|
|
5 |
5 |
8 |
|
|
|
|
|
|
4) log x ≥ |
|
|
5) log |
|
x2 |
>1; |
|
|
6) log |
x2 ≥1. |
|||
|
16 |
2 |
|
|
|
9 |
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||
42. |
Найдите все значения х, при которых совпадают графики |
|||||||||||||
|
функций: |
|
и g(x) = x; |
|
|
2) f (x) =10lg x2 и g(x) = x2 ; |
||||||||
|
1) f (x) = 2log2 x |
|
|
|||||||||||
|
3) f (x) = logx2 |
3 и g(x) = 0,5log|x| 3; |
|
|
|
|
|
|
||||||
|
4) f (x) = logx |
2 и |
g(x) = log5 2. |
|
|
|
|
|
|
|
||||
|
logx |
5 |
|
|
|
наименьшее |
значения |
функции |
||||||
43. |
Найдите |
наибольшее и |
|
|||||||||||
|
y = f (x) на данном промежутке: |
|
|
|
|
1 |
|
|||||||
|
1) f (x ) = log1 |
x, x [1; 4]; |
|
|
2) f (x) = log3 x, x |
|
||||||||
|
|
|
|
; 1 . |
||||||||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
44. |
Постройте график функции: |
|
|
|
|
|
|
|
||||||
|
1°) y = 2 log3 x; |
|
2°) y = log3 x + 3; |
3°) y = log3 (x + 3); |
||||||||||
4)y = − 12 log3 (x + 3); 5) y = 1 + log3 (−x).
45.Дана функция y = log2 (x + 1) .
1°) Найдите ее область определения и множество значений. 2°) Найдите точки пересечения графика функций с осями ко- ординат.
3°) Постройте ее график.
4°) Проходит ли график этой функции через точку А(3; 2);
В − 43 ;2 ?
5)Сколько решений имеет уравнение log2 (x + 1) = x −1 ?
Упражнения для повторения
46. Найдите абсциссы точек пересечения графиков функций:
1) y = х + 2 и y = |
1 |
; |
2) у = х2 + 6 и у = 7х – 4; |
|
x |
|
|
3)y = x2 + x − 2 и у = 2. x + 2
Логарифмы и их применение |
|
|
|
|
|
|
|
45 |
|
||||||
47. |
Решите неравенство: |
|
|
|
|
|
|
|
|
||||||
|
1) |
1 |
|
|
< 0 ; |
|
|
2) 3x2 − 2x −1 ≤ 0 ; |
|
|
|||||
|
−3 + 2x |
|
|
|
|
||||||||||
|
3) |
x |
≤ 3 ; |
|
|
|
|
4)|1 + 2x|> 1. |
|
|
|
||||
48. |
x +1 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Найдите область определения функции: |
|
|
|
|
|||||||||||
|
1) |
y = |
2 |
; |
2) |
y = |
x |
|
; |
3) |
y = −x2 |
+ 3x − 2. |
|||
|
|
x +1 |
x − 2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Итог
Основные понятия
|
|
|
|
|
Символическая |
|
||
Определение |
|
запись, геометриче- |
Применение |
|||||
|
|
|
|
ская интерпретация |
|
|||
Логарифмом числа |
|
|
c = loga b |
Для нахождения |
||||
b > 0 по основанию |
а, |
|
|
aloga b = b. |
корней уравнения |
|||
где a > 0 , а ≠ 1, |
назы- |
|
|
ax = b . |
||||
вается такое число |
с, |
|
|
|
|
|
||
что ac = b . |
|
|
|
|
|
|
|
|
Функция |
вида |
y |
= |
|
|
|
|
Исследование |
|
|
|
|
|||||
= logax, a > 0, a ≠ |
1, на- |
|
|
|
|
показательной |
||
зывается |
логариф- |
|
|
|
|
функции, моде- |
||
мической. |
|
|
|
|
|
|
лирование реаль- |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
ных процессов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Свойства логарифмов
Логарифм |
loga (bc) = loga b + loga c, а > 0,b > 0,с> 0,а ≠ 1 |
||||||
произведения |
|
|
|
|
|
|
|
Логарифм частного |
log |
b |
= log |
|
b − log |
|
c, а > 0, b > 0, с > 0, а ≠ 1 |
|
|
a c |
|
a |
|
a |
|
Логарифм степени |
loga bp = ploga b , p R, b > 0 , a > 0, a ≠ 1 |
||||||
Формула перехода |
loga b = logc b , а > 0, b > 0, с > 0, а ≠ 1, с ≠ 1 |
||||||
к другому основа- |
|||||||
нию |
|
|
logc a |
|
|
||
|
|
|
|
|
|
|
|

46 |
Раздел 1. Показательная и логарифмическая функции |
|
||||
|
Свойства логарифмической функции |
|||||
|
|
|
|
|
|
|
|
|
|
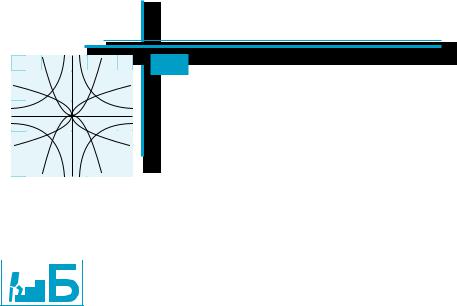
y = loga x, 0 < а < 1 |
|
y = loga x, а > 1 |
|
|
Область определения |
(0; |
+∞) |
|
||
|
Четность |
|
Ни четная, ни нечетная |
|
||
|
Нули |
|
х = 1 |
|
|
|
|
Монотонность |
|
Убывающая |
|
Возрастающая |
|
|
Множество значений |
(–∞; |
+∞) |
|
||
|
Непрерывность |
|
Непрерывна в области определения |
|
||
|
Наибольшее |
|
Не имеет |
|
||
|
и наименьшее значения |
|
||||
|
|
|
|
|
||
§3. Решение показательных и логарифмических уравнений, неравенств и их систем
В этом параграфе рассматриваются некоторые методы решения показательных и логарифмических уравнений, неравенств и их систем.
1. Показательные уравнения и неравенства
 Показательные уравнения и неравенства – это та-
Показательные уравнения и неравенства – это та-
 кие уравнения и неравенства, в которых неизвест- ные содержатся в показателе степени. Простейшее показательное уравнение имеет вид ах = b. Так как функция у = ах монотонная, то каждое свое значение она принимает лишь в од-
кие уравнения и неравенства, в которых неизвест- ные содержатся в показателе степени. Простейшее показательное уравнение имеет вид ах = b. Так как функция у = ах монотонная, то каждое свое значение она принимает лишь в од-
ной точке.
Таким образом, уравнение ах = b при b > 0 имеет единственный корень, который, по определению логарифма, имеет вид x = logаb, а при b ≤ 0 корней не имеет.
Рассмотрим уравнение видааf(x) = аg(x), где а > 0 иа ≠ 1. Оно имеет те же корни, что и уравнение f (x) = g(x) . Фактически этим утвер-
ждением мы пользовались, решая простейшие показательные урав- нения. Оно следует из монотонности показательной функции.
Пример 1. |
Решить уравнение: 1) |
3 9x = 1; 2) 3x2 −3x −1 = |
1 |
. |
|||
|
|||||||
|
|
|
|
27 |
|
||
1) Запишем уравнение в виде: |
3 32x = 1, 31+ 2x = 30. Отсюда |
||||||
1 + 2х = 0, х = –0,5. |
|
|
|
||||
2) Так как |
|
1 |
= 3−3 , то данное уравнение можно записать в |
||||
27 |
|||||||
|
|
|
|
|
|||
виде: 3x2 −3x −1 = 3−3. Это уравнение имеет те же корни, что и уравне-
ние x2 − 3x −1 = −3 . Его корнями, а значит и корнями данного уравнения, являются числа: x1 =1, x2 = 2. g
Ответ. 1) −0,5 ; 2) 1; 2.

48 Раздел 1. Показательная и логарифмическая функции
Уравнение может содержать несколько показательных фун- кций. Тогда их целесообразно выразить через одну.
Пример 2. Решить уравнение 2·3х + 3 + 7·3х – 2 = 493.
Анализируя данное уравнение, можно увидеть, что левую часть легко преобразовать так, что оно будет содержать лишь
одну |
функцию 3х: |
2 33 3x + 7 3−2 3x = 493, 54 3x + |
7 |
3x |
= 493, |
|||||||||
|
|
7 |
|
|
|
|
493 |
|
|
|
|
9 |
|
|
|
54 + |
|
3 |
x |
= 493, |
3 |
x |
= 493, |
3х = 9, 3х = 32, х = 2. g |
|
|
|
||
|
|
|
|
|
|
|
|
|
||||||
9 |
|
9 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответ. 2.
Решение показательных неравенств базируется на использо-
вании монотонности показательных функций. Функции y = ax при a >1 возрастающие, а при 0 < a <1 — убывающие. В соответ-
ствии с этим, неравенство af ( x ) < ag( x ) имеет те же решения, что и неравенство f (x) < g(x) при a >1 и f (x) > g(x) при 0 < a <1 .
Пример 3. Решить неравенство: (0,5)x – 2 < (0,5)1 – x .
Так как 0 < 0,5 <1, то данное неравенство имеет те же реше- ния, что и линейное неравенство x − 2 > 1 − x, или 2x > 3, x >1,5. g
Ответ. (1,5; +∞).
Общими методами решения показательных урав- 
 нений и неравенств являются:
нений и неравенств являются:
— переход от уравнения af ( x ) = ag( x ) (неравенст-
ва af ( x ) < ag( x ) ) к уравнению f(x)= g(x) (неравенству f (x) < g(x) при a >1 и f (x) > g(x) при 0 < a <1 );
— замена переменной;
— разложение на множители;
— логарифмирование обеих частей уравнения или неравенства;
— применение свойств функций.
Проиллюстрируем каждый из этих методов примерами.
Пример 4. Решить уравнение 7х = 9х.
Так как 9х ≠ 0, то, разделив обе части уравнения на 9х, полу-
чим: |
7x |
= 1, |
7 |
x |
7 |
0 |
||||
9 |
x |
|
9 |
|
= |
9 |
|
, x = 0. g |
||
|
|
|
|
|
|
|
|
|||
Ответ. 0. |
|
|
|
|
|
|
||||

Решение показательных и логарифмических уравнений, неравенств |
49 |
Обратите внимание на то, что условие а ≠ 1 при переходе от
уравнения af ( x ) = ag( x ) к уравнению f(x) = g(x) является существен- ным. Равенство 1х = 13 выполняется при любом х, а не только при
х = 3.
|
x2 −3 |
|
x2 −3 |
|
( |
x −1 |
3 |
|
Пример 5. Решить неравенство 2 |
|
5 |
|
− 0,01 |
|
) |
< 0 . |
|
|
|
10 |
|
|
Применяя свойства степени, это неравенство можно предста- вить в виде (2 5)x2 −3 − 10−2 103( x −1) < 0 или 10x2 −3 < 103x −5 . Так как
10 > |
1, то |
последнее неравенство равносильно неравенству |
х2 – 3 |
< 3x – 5, решением которого является интервал (1; 2). g |
|
Ответ. (1; 2). |
||
Пример 6. |
Решить уравнение 4х + 6х – 2·9 х = 0. |
|
Нетрудно заметить, что 4x = (2x )2 , 9x = (3x )2 , 6x = 2x 3x. Так как 9x ≠ 0 ни при каком x R , то, разделив обе части уравнения
на 9 |
x |
, получим равносильное уравнение |
4 |
x |
|
6 |
x |
||
|
|
9 |
|
+ |
9 |
|
− 2 = 0, или |
||
|
|
|
|
|
|
|
|
||
|
2 2x |
|
2 x |
− 2 = 0. После замены |
|
2 x |
||||
|
3 |
|
+ |
3 |
|
|
3 |
|
= y получим квадратное |
|
|
|
|
|
|
|
|
|
|||
уравнение y2 + y − 2 = 0. Корнями этого уравнения являются чи-
сла y = −2, y |
= 1. Таким образом, |
|
2 |
x = −2 |
или 2 |
x |
= 1 . Пер- |
|
1 |
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
вое из этих уравнений решений не имеет, а второе имеет единст- |
||||||||
венный корень x = log2 1 = 0. g |
|
|
|
|
|
|
||
Ответ. 0. |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример |
7. |
Решить неравенство 9х – 4 · 3 х + 3 < 0. |
|
|
||||
Обозначив 3х = t, получим квадратное неравенство t2 – 4t + 3 <
<0. Оно выполняется при 1 < t < 3. Так как 3х = t, то 1 < 3х < 3, или
30 < 3х < 31, 0 < х < 1. g Ответ. (0; 1).
Пример 8. Решить уравнение 2x2 −1 = 34x .
Так как 3 = 2log2 3 , то данное уравнение можно преобразовать
квиду 2x2 −1 = (2log2 3 )4x . Это уравнение равносильно уравнению
50 |
|
|
Раздел 1. Показательная и логарифмическая функции |
||||||||||||||||
x2 −1 = 4x log2 3. Его корнями, а значит и корнями данного урав- |
|||||||||||||||||||
нения, являются числа: 2log2 |
3 ± 4 log22 3 + 1 . |
|
|
|
|
|
|
|
|
||||||||||
Рассмотренное уравнение можно решить логарифмированием |
|||||||||||||||||||
обеих его частей. Прологарифмировав |
|
|
обе |
|
части |
|
уравнения |
||||||||||||
2x2 −1 = 34x |
по основанию 2, получим: x2 −1 = 4x log2 3. g |
|
|
||||||||||||||||
Ответ. |
2log2 3 ± 4 log22 3 + 1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример |
9. |
|
|
|
2 x |
= |
x |
|
− |
5 |
. |
|
|
|
|
|
|
|
|
Решить уравнение |
|
2 |
9 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
Ни одним из рассмотренных |
||||||||||||||
|
|
|
|
|
в предыдущих примерах методов |
||||||||||||||
|
|
|
|
|
решить это уравнение не удается. |
||||||||||||||
|
|
|
|
|
Попробуем найти какое-нибудь |
||||||||||||||
|
|
|
|
|
его решение подбором. В данном |
||||||||||||||
|
|
|
|
|
случае это сделать нетрудно: х = 2, |
||||||||||||||
|
|
|
|
|
ибо |
2 |
2 |
= |
4 |
, |
|
2 |
− |
5 |
= |
4 |
. |
Пока- |
|
|
|
|
|
|
|
|
9 |
|
2 |
9 |
9 |
||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
x |
жем, что других корней уравнение |
||||||||||||||
не имеет. |
|
2 |
является убывающей, |
а функция |
|||||||||||||||
Функция y = |
|
||||||||||||||||||
y = x |
− 5 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
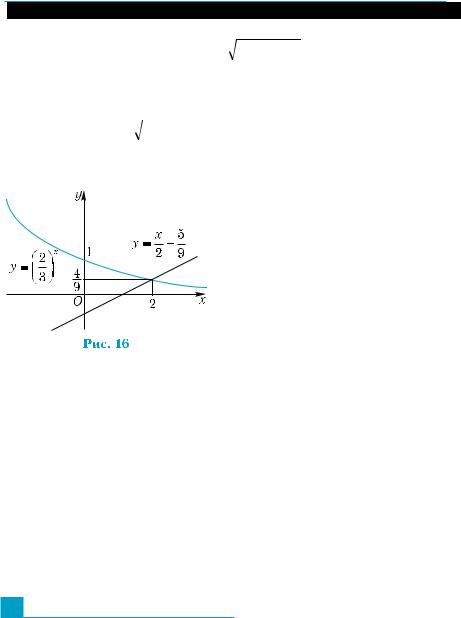
— возрастающей (рис. 16). Поэтому при x > 2 значения |
|||||||||||||||||||
2 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
первой функции меньше 4 |
, а второй — больше |
4 |
; при х < 2, нао- |
||||||||||||||||
|
|
|
9 |
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
борот, значения первой функции больше |
|
4 , а второй — меньше |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
4 . Поэтому графики этих функций не могут иметь точек пересе- |
|||||||||||||||||||
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
чения при х ≠ 2. g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ. |
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
99 Контрольные вопросы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1°. Может ли уравнение ах |
= b иметь два корня? |
|
|
|
|
|
|
||||||||||||
2°. Какие из следующих уравнений не имеют корней: а) 5х = – 2; |
|||||||||||||||||||
б) 5х =0; в) 5х =2? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
