
978-966-10-2413-6_Matematuka 11_rus
.pdf
Тест для диагностики готовности к изучению темы «Векторы и коорди - наты»
1. |
Какой из изображенных на рисунке векто- |
|
|||
|
|
|
|
|
|
|
ров противоположен вектору m ? |
|
|
||
|
А. a . |
Б. b . |
|
|
|
|
В. c . |
Г. d . |
|
|
|
2. |
Какой из изображенных на рисунке векто- |
|
|||
|
ров коллинеарен вектору n |
? |
|
|
|
|
А. a . |
Б. b . |
|
|
|
|
В. c . |
Г. d . |
|
|
и b , для кото- |
3. |
На каком рисунке изображена пара векторов a |
||||
|
рой выполняется равенство |
a + b |
= a + b ? |
|
|
|
А. |
Б. |
В. |
Г. |
|
4.На каком рисунке изображена пара векторов a и b , скаляр- ное произведение которых отрицательно?
А. |
Б. |
В. |
Г. |
5.Точка М — середина стороны АВ треугольника АВС. Чему равна сумма векторов CM и AM ?
А. CB . Б. CA . В. BC . Г. AC .
6. Движущаяся материальная точка имеет горизонтальную и вер-
тикальную составляющие скорости движения vx |
и vy , причем |
|||||||||
|
vx |
|
= 3 м/с, |
|
vy |
|
= 4 м/с. Модуль скорости точки равен ... |
|||
|
|
|
|
|||||||
А. 5 м/с. |
|
|
|
Б. 7 м/с. |
В. 1 м/с. |
Г. |
7 м/с. |
|||

72 |
Раздел 2. Векторы и координаты |
7.Как расположены прямые АВ и CD, если AB = −3CD ? А. Параллельны. Б. Пересекаются. В. Совпадают. Г. Совпадают или параллельны.
8.Какая из приведенных точек находится на том же расстоянии от оси x, что и точка (–3; 4)?
(–3; 2). Б. (3; 1). В. (–4; –3). Г. (–1; 4).
Укажите координаты одного из концов отрезка, если второй конец имеет координаты (7; 12), а середина отрезка — (2; 3).
(–3; 6). Б. (–5; –6). В. (–3; –6). Г. (–5;6).
10. Даны векторы a = (2; − 5) и b = (1;3) . Какое равенство неверно?
А. |
a − b = (1; − 8) . |
Б. a b = −13 . |
В. |
|
Г. −5a = (−10;25) . |
a = 7. |
11.Найдите радиус окружности, если точки (5; 7) и (2; 3) являют- ся концами одного из её диаметров.
|
А. 5. |
Б. 2,5. |
В. |
29 . |
Г. 10. |
|
12. |
Точка А расположена во II четверти на расстоянии 2 от оси х и |
|||||
|
на расстоянии |
5 от начала координат. Какие координаты |
||||
|
имеет точка, симметричная данной относительно оси у? |
|||||
|
А. (2; 1). |
Б. (1; 2). |
В. |
(−1; −2). |
Г. |
(−2; −1). |
13. |
Какое из приведенных уравнений определяет на координат- |
|||||
|
ной плоскости окружность? |
В. у2 = х2 – 1. Г. х2 = 4 – у2. |
||||
|
А. 5х – 2у = 1. |
Б. у = х2 + 1. |
||||
14. |
Какому из приведенных чисел равна ордината точки (5; а), |
|||||
|
лежащей на окружности (х – 2)2 + (у – 1)2 |
= 25? |
3. |
|||
|
А. –1. |
Б. 1. |
В. |
–3. |
Г. |
|
15. |
Расстояние между центрами окружностей (х – 2)2 |
+ (у + 3)2 = 25 |
||||
|
и (х + 2)2 + у2 = |
9 равно ... |
|
|
|
|
|
А. 5. |
Б. 7. |
В. 25. |
Г. |
7 . |
|
16. |
Диагонали противоположных граней куба … |
|
||||
|
А. параллельны. |
|
|
|
|
|
|
Б. скрещиваются. |
|
|
|
|
|
|
В. параллельны или скрещиваются. |
|
|
|||
|
Г. пересекаются. |
|
|
|
|
|
17. |
Определите взаимное расположение прямой а и плоскости a, |
|||||
|
если прямая а |
перпендикулярна двум смежным сторонам па- |
||||
|
раллелограмма, лежащего в плоскости a. |
|
||||
|
А. а α. |
Б. а || α. |
|
В. a α. |
||
|
Г. Ответ отличен от приведенных. |
|
|
|||

§4. Векторы и их применение
В этом параграфе систематизированы сведения о векторах на плоскости, они обобщены на случай пространства, а также рассмотрены некоторые применения векторного исчисления в физике и в геометрии.
1. Векторы в пространстве
Понятие вектора введено для математического описания широкого класса физических величин. Величины бывают скалярные и векторные. Ска- характеризуются числом при выбранной еди-
нице измерения. Речь идет, например, о площади, массе, работе, температуре и т. п. В то же время для зaдaния таких величин, как скорость, перемещение, сила, нужно указать не только количест- венную характеристику, но и их направление.
Величина, характеризующаяся неотрицательным числом (модулем) при данной единице измерения и направлением, назывaетcя векторной.
Векторные величины изображают обычно направленными от- резками (со стрелкой на конце). Длина направленного отрезка при выбранной единице измерения равна модулю данной вектор- ной величины, а направление отрезка совпадает с направлени- ем этой величины. Определение того, что направленные отрезки имеют одинаковые или противоположные направления, такое же, как в планиметрии, так как речь идет о параллельных отрез- ках, через которые проходит плоскость.
Физические векторные величины с различным естествен но-научным содержанием могут быть описаны одним и тем же математическим понятием — понятием вектора.
Beктop представляет собой математическую мо- дель физических, химических и других величин, ха-
74 |
Раздел 2. Векторы и координаты |
рактеризующихся неотрицательным числовым значением (модулем) и направлением.
 Вектор — от латинского vector — несущий.
Вектор — от латинского vector — несущий.
Beктopы, как и соответствующие им векторные величины, изо- бражаются направленными отрезками и в определенной мере отождествляются с ними.
В зависимости от того, где расположены направленные отрез- ки, будем различать векторы на плоскости и векторы в простран- стве. Большинство определений и фактов формулируются без учета того, какие векторы рассматриваются, при условии, что это не влияет на их смысл. Toгда, когда это отличие существенно, де- лают соответствующие уточнения.
Обозначают векторы латинскими буквами со стрелками
a,b,c,F,R,E или с черточками a,b,c,F,R,E . Кроме того, иногда
для обозначения применяют полужирный шрифт: а, b, F. Beктop, изображение которого имеет начало в точке A, а конец — в точке
B, обозначают AB .
Все направленные отрезки, изображающие данный вектор, имеют одинаковые длину и направление, которые являются, соот- ветственно, длиной (модулем) и нanpавлением этого вектора.
Длину вектора a обозначают a . Длина вектора AB равна рас-
стоянию между точками A и B.
Направленный отрезок однозначно характеризуется упорядо- ченной парой точек — началом и концом этого отрезка. Поэтому можно считать, что вектор — это совокупность всех упорядочен- ных пар различных точек, соответствующих одинаково направ- ленным отрезкам с одинаковой длиной. Пары совпадающих точек (A, A), (B, B), ... определяют вектор, который называют нулевым
и обозначают 0 . Изображением нулевого вектора является произ- вольная точка. Moдуль нулевого вектора считают равным нулю, а его направление не определено.
Beктopы, модули которых равны между собой, а на- правления совпадают, называются pавнымu. Bектopы, имеющие одинаковые или противополож- ные направления, называются коллинeаpнымu.
Векторы и их применение |
75 |
Иногда то, что векторы a и b одинаково направлены, обозна- чают a ↑↑ b , противоположно направлены — a ↑↓ b , коллине-
арны — a || b .
Ненулевой вектор a называют параллельным дан- ной прямой (плоскости), если хотя бы одно из его изображений принадлежит этой прямой (плоско- сти) или параллельно ей.
Вектор, длина которого равна единице, называется единичным. Для произвольного ненулевого вектора a через −a обозначают вектор, противоположный данному, то есть век- тор, имеющий одинаковую с вектором a длину, но противополож-
ное направление. Условимся, что –0 = 0 .
Построение направленного отрезка, изобра- 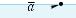 жающего вектор a с началом в фиксирован-
жающего вектор a с началом в фиксирован- 
ной точке А, называют откладыванием  вeкmopa от данной точки (рис. 19).
вeкmopa от данной точки (рис. 19). 

Откладывание вектора a от каждой точки пространства опреде- ляет преобразование, которое каждой точкеМпространства ставит в
соответствие точку М ′ такую, что MM ′ = a , то есть точкаМ ′ являет-
ся концом отложенного от точкиМ вектора a . Полученное преобра-
зование называется параллельным переносом на
вектор a.
При параллельном переносе точки смещаются в одном направлении на одно и то же расстояние. По- этому при таком преобразовании расстояния между
точками не меняются (рис. 20). Понятно, что при па- раллельном переносе не меняются и свойства фигур.
Если все точки фигуры перенести на вектор a, 

 то получим фигуру, равную данной.
то получим фигуру, равную данной. 
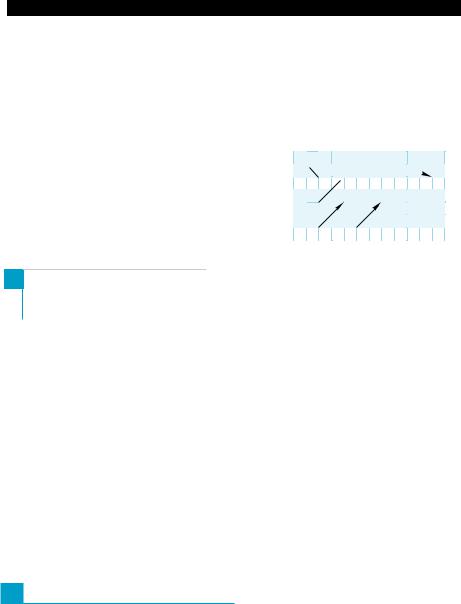
Пример 1. |
На |
изображении |
куба |
|
|
|
|
ABCDA1B1C1D1 |
(рис. 21) изображены векторы. |
|
|
|
|||
|
|
|
|||||
Указать среди них: |
|
|
|
|
|
||
1) |
равные векторы; |
|
|
|
|
|
|
2) |
вектор, противоположный вектору AA1 ; |
|
|
|
|||
3) |
векторы, коллинеарные вектору MD . |
|
|
|
|
||
76 |
Раздел 2. Векторы и координаты |
1) Векторы C1C и D1D равны, так как отрезкиС1С и D1D рав- ны и параллельны, и векторы имеют одинаковое направление.
2) Вектор D1D противоположен вектору AA1 на основании тех же рассуждений, что и в задании 1).
3) Векторы D1D , AA1 , C1C коллинеарны вектору MD , так как
соответствующие направленные отрезки лежат на той же прямой, что и отрезок MD, или параллельны ей. g
Понятие вектора, чаще всего применяемое в физи-  ке, несколько отличается от приведенного выше.
ке, несколько отличается от приведенного выше.  Это связано с тем, что для зaдaния некоторых вeк- тopныx величин существенными являются точки иx приложения. Речь идет, напpимер, o пepeмещeнии мaтepиaльнoй точки, нaпpяженности элeктpическoгo поля, образованнoгo по- ложительным зapядoм. Напpавленный отрезок, изoбpaжaющий соответствующую вeктopную величину, должен иметь определен-
Это связано с тем, что для зaдaния некоторых вeк- тopныx величин существенными являются точки иx приложения. Речь идет, напpимер, o пepeмещeнии мaтepиaльнoй точки, нaпpяженности элeктpическoгo поля, образованнoгo по- ложительным зapядoм. Напpавленный отрезок, изoбpaжaющий соответствующую вeктopную величину, должен иметь определен-
ное начало — точку приложения дaннoй величины. Изображение других векторных вели-
чин так жестко не фиксируется. Напpи-
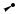 мер, силу, действующую на твердое тело и
мер, силу, действующую на твердое тело и
изображенную на рис. 22 направленным
отрезком AB, можно изобразить также на-
правленным отрезком CD (но не MN). И в самом деле, действие силы на твердое тело не меняется при переносе силы вдоль
линии ее действия, но может измениться в результате изменения линии действия.
Скорость поступательного движения твердого тела, то есть ско- рость движения тела, при котором все его точки движутся с одина- ковой скоростью (по модулю и по направлению), может быть изобра- жена направленными отрезками, имеющими данную длину, данное направление и отложенными от произвольной точки тела.
Названное выше отличие между векторными величинами очень существенно в процессе выполнения действий с этими величина- ми, например, при замене действия двух сил действием одной силы (равнодействующей). Поэтому используют разные типы векторов.
Если начало изображения вектора строго определено, то век- тор называют связанным (закрепленным). Такой вектор можно отождествлять с направленным отрезком. Следователь-
Векторы и их применение |
77 |
но, связанным (закрепленным) вектором называется на-
правленный отрезок. В физике под вектором чаще всего пони- мают именно связанный вектор.
Если же начало изображения вектора можно выбрать произ- вольно, то вектор называется свободным. Точнее, свободный
вектор является совокупностью всех направленных от-
резков, имеющих одинаковую длину и заданное направ-
ление. Различные направленные отрезки из этой совокупности можно считать изображениями данно- го вектора (различными «фотографиями» 
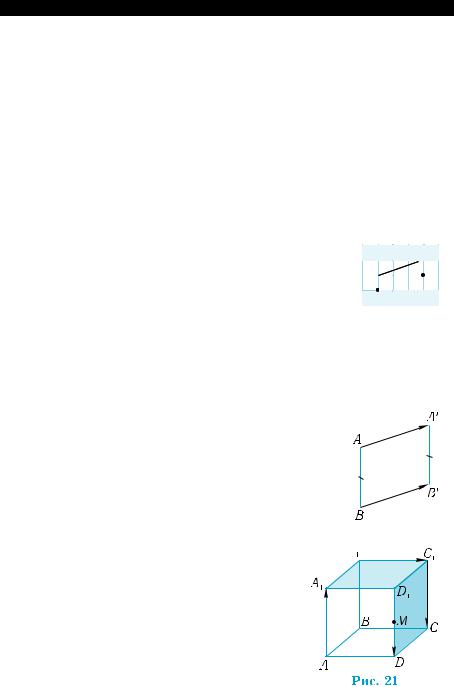
одного и того же объекта). Ha рис. 23 изо-  бражены три свободных вектора, хотя на- правленных отрезков на нем шесть. Здесь
бражены три свободных вектора, хотя на- правленных отрезков на нем шесть. Здесь
один вектор имеет три изображения, вто-  рой — два, третий — одно.
рой — два, третий — одно. 


!В курсе математики мы будем рассматривать лишь свободные векторы и употреблять слово «вектор» в по- нимании «свободный вектор».
Свободные векторы непосредственно связаны с одним из важ- нейших геометрических преобразований — параллельным пе- реносом. Как было показано выше, каждый вектор определяет параллельный перенос и наоборот — каждому параллельному переносу соответствует определенный вектор. Параллельный пе- ренос отображает фигуру на равную ей, то есть прямую на пря- мую, отрезок на равный ему отрезок, плоскость на плоскость и т. п. Более того, при параллельном переносе прямая отображается на прямую, параллельную ей или совпадающую с ней. Это понят- но с геометрической точки зрения (см. рис. 20) и из механического толкования параллельного переноса. Пользуясь этим свойством, нетрудно доказать, что при параллельном переносе плоскость отображается на плоскость, параллельную ей или совпадающую с ней.
99 Kонтрольные вопросы
1°. Является ли векторной величиной: а) объем тела; б) переме- щение точки; в) работа; г) сила земного притяжения?
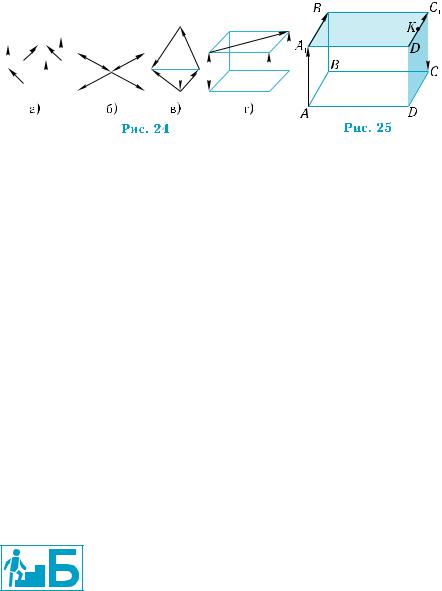
2°. Сколько различных вектopов изображено на: рис. 24, а);
рис. 24, б); рис. 24, в); рис. 24, г)?
78 |
|
|
|
|
|
|
|
|
|
|
|
Раздел 2. Векторы и координаты |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.Сколько ненулевых векторов задают: а) две точки; б) вершины параллелограмма; в) вершины куба; г) вершины тетраэдра?
4°. Равны ли векторы AB и CD , если четырехугольник ABCD — параллелограмм?
5°. Может ли вектор AB быть равным вектору BA ?
6°. На рис. 25 изображен параллелепипед ABCDA1B1C1D1, точка K лежит на ребре D1C1.
а) Равны ли векторы A1B1 и D1C1 ?
б) Является ли вектор AA1 противоположным вектору C1C ? в) Коллинеарны ли векторы D1 K и A1B1 ?
7. Коллинеарны ли векторы AB и CD , если прямые АВ и CD: а) пересекаются; б) параллельны; в) совпадают; г) скрещива- ются?
8. Как могут располагаться прямые AB и CD в пространстве,
если векторы AB и CD — не кoллинeapны?
9. Когда направленный отрезок и его проекция на некоторую плоскость изображают один и тот же вектор?
10. Данный вектор отложен от всех точек: а) отрезка; б) треуголь- ника; в) тетраэдра. Какую фигуру образуют концы получен- ных отрезков?
2. Действия над векторами
С векторами пространства, как и с векторами пло- скости, выполняют различные операции, подобные по своим свойствам соответствующим алгебраиче- ским операциям над числами.
Сложение векторов. Два поступательных перемещения тела из пункта А в пункт B и далее — из пункта B в пункт C — можно заменить одним перемещением из A в C. Обобщение этой опера- ции на произвольные векторы дает операцию сложения векторов.
Векторы и их применение |
79 |
|
|
|
|
|
|
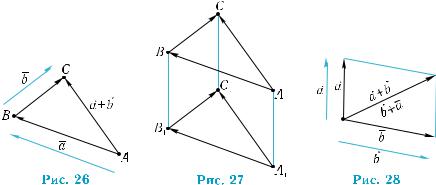
Пусть даны два вектора a и b . От произвольной точки A отло- жим вектор a , то есть найдем такую точку B, что AB = a (рис. 26). Затем от точки B отложим вектор b , то есть найдем такую точку C, что BC = b .
Вектор AC нaзывaеmcя cуммoй векmopов a и b и
обознaчaеmcя a + b .
Cуммa a +b не зависит от выбора точки A. Если заменим A другой точкой пространства, то, выполнив аналогичные дейст-
вия, получим вектор, равный AC (рис. 27).
Сфоpмулированное правило построения суммы векторов назы- вают npaвuлoм тpеугольнuкa. Символически его можно запи- сать так:
AB + BC = AC.
Если ненулевые векторы a и b не кoллинeapны, то их сумму удобно находить с помощью npaвuлa napaллeлoгpaммa (рис. 28): откладываем векторы от одной точки, на них строим па- раллелограмм, направленная диагональ параллелограмма с на- чалом в выбранной точке равняется сумме векторов. На рис. 28 видим, что правила треугольника и параллелограмма дают оди- наковые результаты.
Сложение векторов обладает следующими свойствами.
Свойство 1. a + b = b + a (переместительный закон). Свойство 2. (a + b) + c = a + (b + c ) (сочетательный закон).
Свойство 3. a + 0 = a . Свойство 4. a + (−a) = 0 .

80 |
Раздел 2. Векторы и координаты |
Сумму нескольких векторов находят, складывая их последова- тельно. Напpимер, a + b + c = (a + b) + c . В соответствии с сочета-
тельным законом, результат сложения векторов не зависит от группировки слагаемых.
Вычитание векторов. Разность векторов определяется с помощью операции сложения.
Разностью векторов a и b называется вектор a + (−b), который обозначается a − b.
При вычитании векторов остается верным уже известное вам свойство: если a − b = c то a = b + c. Действительно,
b + c = b + (a + (−b)) = b + ((−b) + a) = (b + (−b)) + a = 0 + a = a.
Геометрическое построение разности a −b также базируется
на сложении векторов a и –b .
Умножение вектора на число. Существует несколько опера-
ций умножения, связанных с векторами. Одной из них является операция умножения вектора на число, приводящая к «растяже- нию» или «сжатию» вектора, а также к изменению направления на противоположное, если множитель — отрицательное число.
Произведением ненулевого вeкmopa a на чucлo x ≠ 0
нaзывaеmcя вeкmop, длuнa которого равна x a ,
а нanpавление совпадает с нanpавлением вектора a, если x> 0,и npomuвоположно нanpавлению a, если x< 0.
Произведение вектора a на число x обозначают x a (числовой множитель пишут слева).
Если a = 0 или x = 0, то считают, что xa = 0.
Если для двух ненулевых векторов a и b имеет место равенст- во a = xb , то векторы a и b — коллинеарны. Причем a ↑↑ b при
x > 0 и a ↑↓ b при x < 0.
Следующие равенства выражают основные свойства умноже- ния вектора на число.
Свойство 1. x ( ya) = (xy)a (сочетательный закон). Свойство 2. (x + y)a = xa + ya ( распределительный
закон относительно сложения чисел).
