
978-966-10-2413-6_Matematuka 11_rus
.pdf
Интеграл |
221 |
Задачу о нахождении пути, пройденного прямолинейно дви-
жущейся точкой, можно свести к задаче о нахождении площади некоторой фигуры.
Рассмотрим сначала случай равномерного движения точки со скоростью v = v0. Графиком зависимости скорости от времени в системе ко-  ординат (t; v) будет прямая v = v0,параллель-
ординат (t; v) будет прямая v = v0,параллель-
ная оси t. Путь s, пройденный точкой за про-
межуток времени [t0; T], равен s = v0(T – t0), то  есть площади затушеванного прямоугольника
есть площади затушеванного прямоугольника 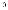
(рис. 134). Таким образом, путь, пройденный
точкой при равномерном движении, равен площади фигуры, огра-
ниченной графиком зависимости скорости от времени, осью абсцисс и двумя вертикальными прямымиt = t0 и t = T.
Рассмотрим теперь случай неравномерного движения. Пусть материальная точка движется прямолинейно со скоростью
v = v(t), график которой изображен на рис. 135, а). Найдем путь, пройденный точкой за промежуток времени [t0; T]. Мы уже умеем находить путь в случае равномерного движения. Чтобы восполь- зоваться этим, разобьем промежуток времени [t0; T] на меньшие промежутки [t0; t1], [t1; t2] и т. д. (рис. 135, б). На каждом из по- лученных промежутков (так как они небольшие) движение мож- но считать равномерным со скоростью, равной скорости точки в начальный момент рассматриваемого промежутка. Тогда путь, пройденный точкой за промежуток времени [t0; t1], приближенно равен v(t0)(t1 – t0), то есть площади затушеванного прямоугольни- ка с основанием (t1 – t0) ивысотой v(t0) (рис. 135, в).
Аналогичные рассуждения можно провести для каждого про- межутка. Поэтому весь путь, пройденный точкой за промежуток времени [t0; T], приближенно равен площади затушеванной сту- пенчатой фигуры (рис. 136).
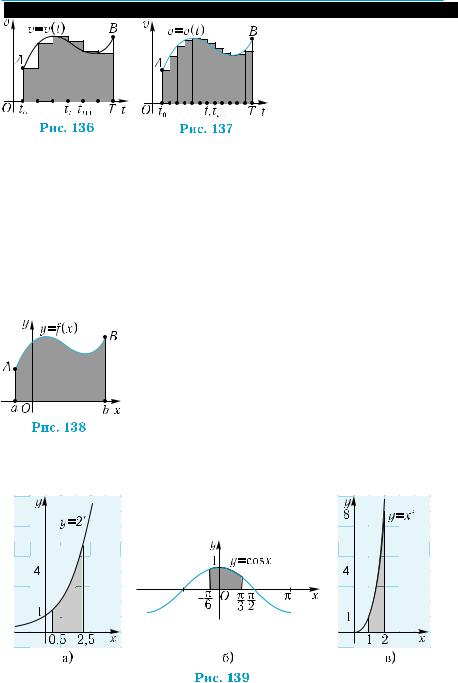
222 |
Раздел 4. Интеграл и его приложения |
|
|
Для того, чтобы вы- |
|
|
числить путь точнее, не- |
|
|
обходимо разбить проме- |
|
|
жуток [t0; T] на большее |
|
|
число промежутков мень- |
|
|
шей длины (рис. 137). |
|
|
Из |
геометрических |
|
сооб ражений ясно, что |
|
при увеличении числа промежутков ступенчатая линия прибли- |
||
жается к графику функции v = v(t), а площадь ступенчатой фигу- |
||
ры все меньше и меньше отличается от площади фигуры t0АВT, |
||
ограниченной графиком зависимости скорости v = v(t) от времени, |
||
отрезком оси [t0; T] и отрезками вертикальных прямых t = t0 и t = T |
||
(рис. 136, 137). |
|
|
Поэтому естественно считать, что путь, пройденный точкой за |
||
промежуток времени [t0; T], равен площади фигуры t0АВT. |
||
Воспользуемся теперь полученным результатом для вычисле- |
||
ния площадей некоторых фигур. |
задананепрерыв- |
|
|
Пусть на промежутке [a;b] |
|
|
ная неотрицательнаяфункция y = f (x) . |
|
|
Фигура, ограниченная графиком фун- |
|
|
кции y = f(x), отрезком [a; b] оси х и от- |
|
|
резками прямых х = а, х = b, называет- |
|
|
ся криволинейной трапецией (рис. 138). |
|
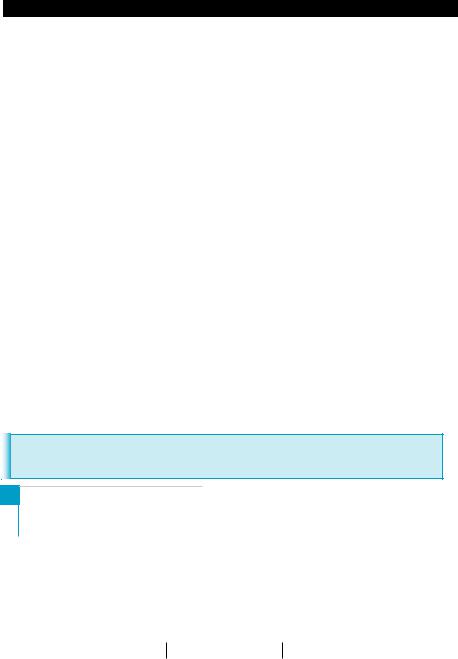
Примеры некоторых криволинейных трапеций представлены на рис. 139.

224 |
|
|
|
|
|
|
|
|
|
|
Раздел 4. Интеграл и его приложения |
|
|
|
|
|
|
|
|
|
|
1 |
π |
|
|
|
|
|
|
|
|
|
|
2 |
|
Пример |
|
|
1. |
|
Вычислить: 1) ∫ x2dx ; 2) ∫ cos xdx . |
||||||
|
|
|
|
|
|
|
|
|
|
−1 |
0 |
1) Одной из первообразных для подынтегральной функции |
|||||||||||
у = х2 на отрезке [–1; 1] является функция у = x3 . Следовательно, |
|||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
3 |
1 |
|
3 |
|
1 |
|
3 |
2 . |
|
|||
∫ x2dx = x |
|
|
|
= |
− (−1) |
= |
|
||||
−1 |
3 −1 |
|
3 |
3 |
|
|
3 |
|
|||
π |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
π |
= sin π − sin 0 = sin π = 1 . g |
|||
2) ∫cos xdx = sin x 02 |
|||||||||||
0 |
|
|
|
|
2 |
|
|
|
|
2 |
2 |
Ответ. 1) |
; 2) 1. |
|
|
|
|
||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
На основании рассмотренных выше задач интеграл имеет про- |
|||||||||||
стой физический и геометрический смысл. |
|||||||||||
|
|
|
|
|
|
T |
|
|
|
|
|
Интеграл òv(t)dt при v(t) ≥ 0 равен пути, пройденно- |
|||||||||||
|
|
|
|
|
|
t0 |
|
|
|
|
|
му материальной точкой, движущейся прямолинейно |
|||||||||||
со скоростью v = v(t), за промежуток времени [t0; T]. |
|||||||||||
|
|
|
|
|
|
b |
|
|
|
|
|
Интеграл ò f (x)dx |
от неотрицательной непрерывной |
||||||||||
|
|
|
|
|
|
a |
|
|
|
|
|
на отрезке [a; b] функции y = f(x) равен площади кри- |
|||||||||||
волинейной трапеции, ограниченной графиком этой |
|||||||||||
функции и отрезками прямых у = 0, х = а, х = b. |
|||||||||||
Пример |
|
|
2. |
|
Найти |
|
площадь |
криволиней- |
|||
ной трапеции, ограниченной графиком функ- |
|||||||||||
ции у = х2 |
|
и отрезками прямых |
у = 0, х = –1, |
||||||||
х = 2. |
|
|
|
|
|
|
|
|
|
|
|
Изобразим фигуру, площадь которой |
|||||||||||
нужно вычислить (рис. 140). Это криволиней- |
|||||||||||
ная трапеция. Поэтому ее площадь, согласно |
|||||||||||
геометрическому смыслу интеграла, равняет- |
|||||||||||
2 |
2 |
dx |
= |
x3 |
2 |
1 |
3 |
3 |
) = 3. g |
||
ся S = ∫ x |
|
3 |
= |
3 |
(2 |
− (−1) |
|||||
−1 |
|
|
|
|
|
−1 |
|
|
|
||
Ответ. 3. |
|
|
|
|
|
|
|
||||
Интеграл |
|
|
|
|
225 |
|
Пример 3. |
Материальная точка движется прямолинейно со |
|||||
скоростью v = |
2sin t, где v – скорость, м/с; t – время, с. Какой путь |
|||||
пройдет точка за промежуток времени [0; p]? |
|
|
||||
Согласно физическому смыслу интеграла имеем: |
|
|||||
|
π |
|
|
|
|
|
|
s = ∫2sintdt = −2cost|0π = −2(cos π − cos0) = 4 (м). g |
|||||
Ответ. 40м. |
|
|
|
|
||
|
|
Задачи на нахождение пути, пройденного матери- |
||||
|
|
альной точкой, и площади криволинейной трапеции |
||||
|
|
привели нас к рассмотрению сумм специального |
||||
|
|
вида. Действительно, если промежуток [t0 ,T ] разде- |
||||
лить нап равных промежутков длиной |
t = T − t0 |
, то путь, пройден- |
||||
|
|
|
|
n |
|
|
ный точкой за произвольный промежуток [ti −1 ,ti ] |
, приближенно ра- |
|||||
вен v(ti–1)Dt, i = 1, 2, ...,п. Тогда весь путь приближенно равен сумме |
||||||
|
|
sn = v(t0 ) t + v(t1 ) |
t + ... + v(tn −1 ) t . |
|
||
Чем меньшим будет дробление промежут- |
|
|
||||
ка[t0 |
,T ] , то есть чем большим будет п, тем бо- |
|
|
|||
лее точный получим результат. Аналогичные |
|
|
||||
рассуждения можно проводить при вычисле- |
|
|
||||
нии площади криволинейной трапеции. Пло- |
|
|
||||
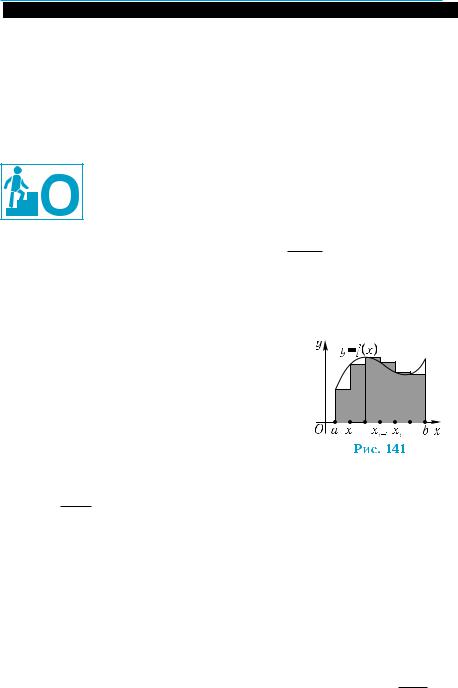
щадь криволинейной трапеции на рис. 141 |
|
|
||||
приближенно |
равна площади |
ступенчатой |
|
|
||
фигуры, то есть сумме |
|
|
x , |
|
||
|
|
Sn = f(a) x + f (x1 ) |
x + ... + f (xn−1 ) |
|
||
где |
x = b − a . |
|
|
|
|
|
|
n |
|
|
|
|
|
Если п устремить к бесконечности, получим точное значение |
||||||
искомой площади. Как известно, площадь рассматриваемой криво- |
||||||
|
|
|
|
b |
|
|
линейной трапеции равна интегралу ò f (x)dx . Следовательно, ин- |
||||||
|
|
|
|
a |
|
|
теграл равен пределу последовательности сумм Sn при n, стремя- |
||||||
щемся к бесконечности. Обобщим изложенное. |
|
|
||||
Пусть на промежутке [а; b] задана непрерывная функция |
||||||
у = f(x). Разобьем промежуток [а; b] на n равных частей точками х1, |
||||||
х2, ..., хп–1. Длина каждого полученного отрезка равна |
x = b − a . |
|||||
|
|
|
|
|
|
n |
226 |
Раздел 4. Интеграл и его приложения |
Сумма вида Sn = f(a) x + f (x1 ) x + ... + f (xn−1 ) x называется ин- |
|
тегральной суммой для функции у= f(x) на промежутке [а; b]. |
|
|
b |
Интеграл ò f (x)dx равен пределу интегральных сумм |
|
|
a |
для функции y = f(x) при n, стремящемся к бесконеч- |
|
ности. |
|
На основании этого вычисление интеграла рассматривают как |
|
некоторый процесс суммирования, то есть объединение отдель- |
|
ных частей в целое. Символ интеграла — это продленная буква |
|
S — первая буква латинского слова «sum» (сумма). |
|
|
С помощью интегральных сумм при- |
|
ближенно вычисляют различные величи- |
|
ны. Например, площадь криволинейной |
|
трапеции, если функция у = f(x) задана |
|
графически или с помощью таблицы. |
|
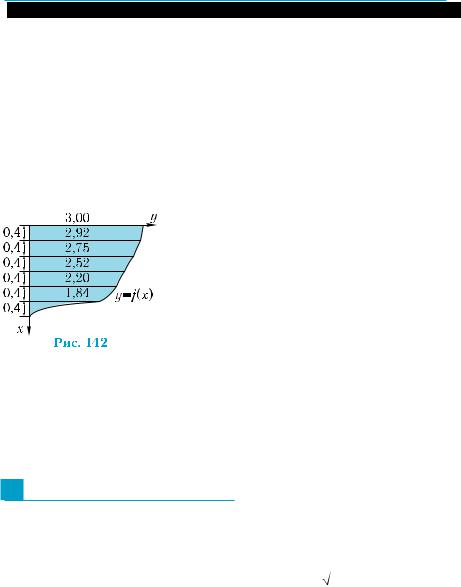
Так, для вычисления площади попереч- |
|
ного сечения корпуса судна (рис. 142) |
|
можно действовать следующим образом. |
|
2,4 |
Интеграл |
ò f (x)dx , равный половине искомой площади S, за- |
|
0 |
меняют его интегральными суммами, выполнив сначала нужные |
|
измерения: |
S ≈ 3 0,4 + 2,92 0,4 + 2,75 0,4 + 2,52 0,4 + 2,20,4 + |
|
2 |
+ 1,840,4 ≈ 6,1 (м2). Вся площадь приближенно равна 12,2 м2. |
|
99 Контрольные вопросы
1°. Какие из фигур, изображенных на рис.143, а)–г), являются криволинейными трапециями? Выразите их площади с помо- щью интеграла.
1
2°. Каков геометрический смысл интеграла ò xdx ?
0
3°. На рис. 144 изображен график зависимости скорости тела, движущегося прямолинейно, от времени. За какой промежу- ток времени: [0; 1] или [1; 2] — тело прошло больший путь?
4°. Две материальные точки движутся прямолинейно, причем скорость движения первой точки v = t2 , а скорость второй –

Интеграл |
227 |
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v = t . Какая из точек пройдет больший путь за промежуток |
|||
|
времени: а) [0, 1]; б) [1; 2]? |
|
|
|
5°. |
Зависит ли значение интеграла от выбора первообразной для |
|||
|
подынтегральной суммы? |
|
|
|
|
a |
|
|
|
6°. |
Чему равен интеграл ò f (x)dx , если график функции у = f(x) |
|||
|
b |
4; 2) а = –4, b = 4? |
||
|
изображен на рис. 145 и: 1) а = 0, b = |
|||
|
2 |
|
|
|
7. |
Известно, что ∫ f (x)dx = 3 , у = F(x) — первообразная для фун- |
|||
|
−1 |
|
|
|
|
кции у = f(x) и F(2)= 1. Чему равно значение функции у = F(x) |
|||
|
в точке х = –1? |
|
|
|
|
a |
b |
||
8°. |
Чему равен интеграл ò f (x)dx , если |
ò f (x)dx = 1? |
||
|
b |
a |
||
|
a |
|
|
|
9°. |
Чему равен интеграл ò f (x)dx ? |
|
|
|
|
|
|
||
a
3
10.Чему равен интеграл ò f (x)dx , если гра-
фик первообразной у =0F(x) для функции  у = f(x) изображен на рис. 146?
у = f(x) изображен на рис. 146?

228 |
Раздел 4. Интеграл и его приложения |
2. Свойства интеграла
Из определения интеграла и правил нахождения первообразной вытекают следующие свойства ин- теграла, упрощающие его вычисление.
Свойство 1. Интеграл от суммы функций равен сум- ме интегралов от этих функций, то есть
b |
b |
b |
∫(f (x) + g(x))dx = ∫ f (x)dx +∫ g(x)dx . |
||
a |
a |
a |
Действительно, пусть y = F(x), y = G(x) – первообразные для |
||
функций y = f (x) и y = g(x) |
на отрезке [a;b] . Тогда функция |
|
y = F(x) + G(x) являетсяпервообразнойдляфункции y = f (x) + g(x) на этом промежутке. Согласно определению интеграла
b
∫( f(x) + g(x))dx = ( F(x) + G(x)) ba = ( F(b) + G(b)) − ( F(a) + G(a)) =
a
|
b |
b |
= ( F(b) − F(a)) + (G(b) − G(a)) = ∫ f(x)dx + ∫ g(x)dx. g |
||
|
a |
a |
Нетрудно доказать, что свойство 1 справедливо для суммы лю- |
||
бого конечного числа слагаемых. |
|
|
Свойство 2. Постоянный множитель можно выно- |
||
сить за знак интеграла, то есть |
|
|
b |
b |
|
∫kf (x)dx = k∫ f (x)dx . |
|
|
aa
Действительно, пусть y = F(x) — первообразная для фун- кции y = f (x) на отрезке [a;b] . Тогда y = kF(x) является перво образной для функции y = kf (x) на данном промежутке. Согла- сно определению интеграла, имеем
b |
|
|
|
|
|
|
ba = k( F |
|
|
|
|
|
|
|
b |
|
|
|
|
|
∫kf(x)dx = kF(x) |
|
(b) − F(a)) |
= k∫ f (x)dx . g |
|
|
|||||||||||||||
|
|
|
||||||||||||||||||
a |
|
|
|
|
4 |
|
|
|
|
|
3 |
|
|
a |
1 |
e2x − ex |
|
|||
Пример 4. |
|
|
|
|
9x |
2 |
− |
x |
+ 1 |
|
dx . |
|||||||||
Вычислить: 1) ∫ |
|
|
2 |
dx ; 2) |
∫ |
e |
x |
|||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
0 |
|
|
||||
1) Используя последовательно свойства 1 и 2 интеграла, по- |
||||||||||||||||||||
лучим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
9x |
2 |
− |
3 |
|
4 |
2 |
|
|
4 |
3 |
|
4 |
|
|
|
|
|||
∫ |
|
2 |
x +1 dx = |
∫9x |
|
dx − ∫ |
2 |
xdx + ∫dx = |
|
|
||||||||||
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
1 |
|
|
|
|
||||

230 |
|
|
|
|
|
|
|
|
|
Раздел 4. Интеграл и его приложения |
||||||||
|
Заметим, что 2х – 3 ≤ 0 при x ≤ |
3 |
и 2х – 3 ≥ 0 при x ≥ 3 . Поэ- |
|||||||||||||||
|
3 − 2x |
x ≤ 3 , |
|
2 |
|
|
|
|
|
2 |
||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
2 |
Чтобы избавиться от знака моду- |
||||||||
тому 2x − 3 = |
|
|
|
|
|
|
|
|||||||||||
|
2x − 3 |
x ≥ 3 . |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ля в подынтегральной функции, разобьем промежуток [0; 2] на |
||||||||||||||||||
|
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
два промежутка 0; |
2 |
и |
|
|
2 |
;2 . Воспользовавшись свойством 3 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
интеграла, получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
3 |
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||
|
∫ 2x − 3 dx = ∫ 2x − 3 dx + |
∫ 2x − 3 dx = ∫(3 |
− 2x)dx + ∫(2x − 3)dx = |
|||||||||||||||
|
0 |
0 |
|
|
|
|
3 |
|
|
|
|
|
0 |
|
|
3 |
|
|
|
3 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= (3x − x2 ) 2 + (x2 − 3x )23 = 2,5. |
|
|
|
|
|
|
|
|
||||||||||
|
0 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ. 2,5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 6. |
Вычислить площадь фигуры, ограниченной лини- |
|||||||||||||||||
ями у = х, у = 1 |
, х = е, у = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x |
|
Изобразим фигуру, площадь которой нуж- |
|||||||||||||||
|
|
|
||||||||||||||||
|
|
но найти (рис. 148). Это криволинейная трапе- |
||||||||||||||||
|
|
ция. Однако сверху она ограничена графиком |
||||||||||||||||
|
|
функции |
y = f (x) , которая на различных проме- |
|||||||||||||||
|
|
жутках задается различными формулами: |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
0 ≤ x ≤ 1, |
|
|
|||
|
|
|
|
|
|
|
|
|
f (x) = |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
1 |
1 ≤ x ≤ e. |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
e |
|
|
|
1 |
|
|
|
e |
dx |
|
x2 1 |
e |
1 |
+ 1 = |
3 |
. |
|
|
Тогда S = ∫ f (x)dx = ∫ xdx + ∫ |
x |
= |
2 |
+ ln x 1 = |
2 |
2 |
|||||||||||
|
0 |
|
|
|
0 |
|
|
|
1 |
|
0 |
|
|
|
||||
|
Ответ. 1,5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
99 |
Контрольные вопросы |
|
|
|
|
|
|
|
|
|||||||||
|
|
a |
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
1°. |
Известно, что ∫ f (x)dx = 1, |
∫ g(x)dx = 3. |
Чему равен интеграл: |
|||||||||||||||
|
a |
0 |
|
|
|
|
|
|
|
0 |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
а) ∫ (2f (x) − 4g(x))dx; |
|
|
|
|
|
б) ∫ ( f (x) + 1)dx ? |
|
|
|||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
